Соединения без повторений
| Соединение предметов | ||
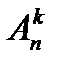
| 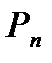
| 
|
| Размещение из n элементов по k элементам (важен порядок и важны сами элементы) | Перестановка n элементов без повторения (важен порядок, элементы не важны) | Сочетание из n элементов по k элементам (важны элементы, порядок не важен) |
Определение: Введем множество N0=NÈ{0}.Пусть элементы k, n ÎN0, причем k£n. Размещением из n элементов множества В={b1, b2,…, bn} по k элементам будем называть всякую последовательность, составленную из неповторяющихся элементов множества В, имеющую длину k
(а1, а2, …, аk).
Пример: А={1,2,3}. Выпишем все размещения из трех элементов по 2
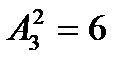 (1,2); (1,3); (2,1); (2,3); (3,1); (3,2)
(1,2); (1,3); (2,1); (2,3); (3,1); (3,2)
ТеоремаПусть дано множество В={b1, b2,…, bn} k, n ÎN0, k£n. Число размещений из n элементов по k элементам без повторений можно вычислить по формуле:
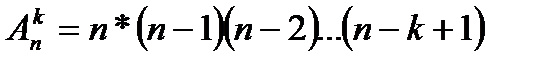 =
= 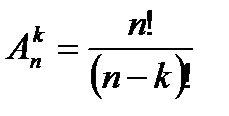
Для доказательства воспользуемся принципом умножения. Для построения каждого размещения нужно рассмотреть последовательность из n элементов. На первом месте n возможностей, на втором n-1.
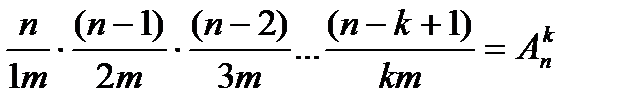
Пусть (n-k)!=1*2*3*…(n-k) n!=1*2*3*…*(n-k)*(n- k +1)*…*n
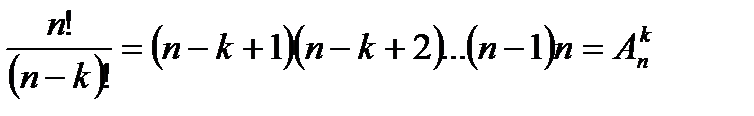
Определение: Пусть N0=NÈ{0}, k, n ÎN0, k£n, В={b1, b2,…, bn}. Сочетаниемиз n элементов по k элементам без повторений будем называть всякое подмножество множества В, состоящее из k неповторяющихся элементов заданного множества В.
Пример: А={0,1,4}. Выпишем все размещения из трех элементов по 2
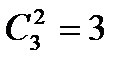 {0,1}; {1,4};{ 0,4}
{0,1}; {1,4};{ 0,4}
ТеоремаПусть k, n ÎN0, k£n, В={b1, b2,…, bn}. Число сочетаний из n элементов по k элементам можно подсчитать используя формулу: 
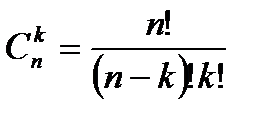
Рассмотрим формулу из предыдущей теоремы. Число размещений равно 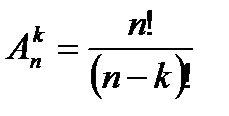 . Ясно, что число размещений
. Ясно, что число размещений 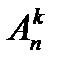 можно связать с числом сочетаний формулой
можно связать с числом сочетаний формулой 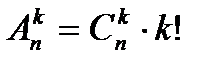 .
. 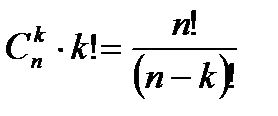 следовательно
следовательно 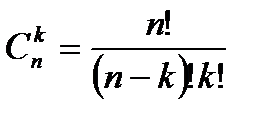 .
.
Задача: Сколькими способами можно рассадить 4 учащихся на 25 местах.
I способ (принцип умножения)
25*24*23*22=303600
II способ (размещение)
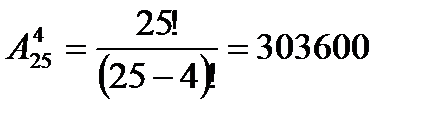
Задача: Учащемуся необходимо сдать 4 экзамена на протяжении 8 дней. Сколько способов? Решить задачу если известно, что последний экзамен будет сдаваться на 8 день.
1) 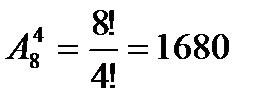
2) 4* 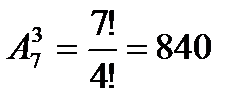
Задача: Сколькими способами читатель может выбрать 3 книги из 5.
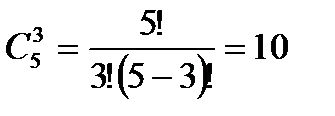
Задача: В турнире принимали участие n шахматистов, каждые два шахматиста встретились 1 раз. Сколько партий было в турнире?
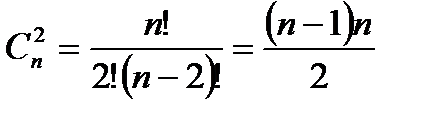
Определение: Пусть n ÎN0, В={b1, b2,…, bn}. Перестановкой n элементов множества В будем называть всякое размещение без повторений из n элементов по n элементам.
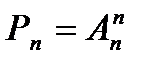
Теорема 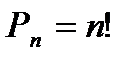 . Число перестановок n элементов множества равно n! n ÎN0, В={b1, b2,…, bn}.
. Число перестановок n элементов множества равно n! n ÎN0, В={b1, b2,…, bn}.
Пусть 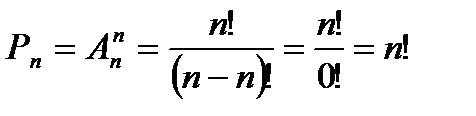
Следствие: n, k ÎN0, k£n, В={b1, b2,…, bn}. Число размещений из n элементов по k элементам модно вычислить по формуле:
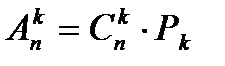
Задача: Сколькими способами можно разместить в очередь 7 человек.
N=7 Р7=7!
Задача: Сколькими способами можно упорядочить множество 1, 2, 3, …, 2n, так чтобы каждое четное число имело четный номер.
А={1, 2, 3, …, 2n} n!*n!=(n!)2.
Задача: Сколько можно составить перестановок из n элементов, в которых данные два элемента не стоят рядом.
n!-(n-1)!2!=(n-1)!(n-2)
Свойства сочетаний
1° 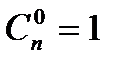 2°
2° 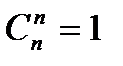 3°
3° 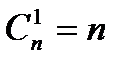
4° 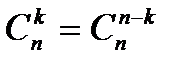 5°
5° 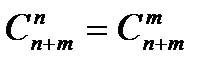 6°
6° 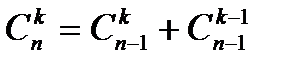 7°
7° 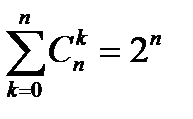 ( из7)
( из7)
Из св 6 можно последовательно находить 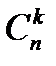 зная
зная 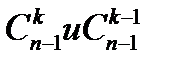 . в виде треугольника Паскаля:
. в виде треугольника Паскаля:
Формула бинома Ньютона
(а+b)n= 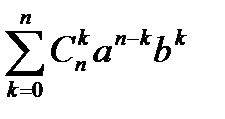 (можно доказать по индукции)
(можно доказать по индукции)
Перемножим (а+b) само на себя n раз, получим сумму, содержащую 2n слагаемых, каждое слагаемое представляет произведение d1*d2*…*dn, где di либо а, либо b, 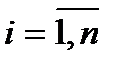 , полученную сумму разобьем на n+1 слагаемых В0, В1, …Вn.
, полученную сумму разобьем на n+1 слагаемых В0, В1, …Вn.
Пусть у нас в группе Вk содержатся те произведения, в которых элемент b встречается k раз, а элемент a встречается (n-k) раз.
Дата добавления: 2017-08-01; просмотров: 831;
