Отношение эквивалентности

Предварительно определим два таких понятия.

Покрытие множества– это совокупность его подмножеств, совместно накрывающих это непустое множество: 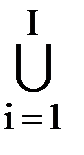М_i = M, М ¹ Æ.

Например, {M₁, M₂} является покрытием множеств M₁ È M₂.

Разбиение множества – частный случай покрытия, когда составляющие подмножества попарно не пересекаются: 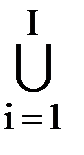М_i = M,

M_i1 Ç M_i2 ( i₁ ¹ i₂) = Æ.

Например, для универсального множества:

E = { М₁ Ç М₂, М₁ Ç М₂¢, М₁¢ Ç М₂, М₁¢ Ç М₂,¢}_r.

Здесь индекс «r» («разбивание») обязателен, иначе получается неравенство мощностей слева и справа (справа – всего 4). В подмножествах разбиения каждый элемент M представлен только один раз.

Отношение эквивалентности– это первое замечательное теоретико-множественное отношение. Оно обладает тремя свойствами: рефлексивность, симметричность и транзитивность. По-другому говорят: любое РСТ-отношение – это отношение эквивалентности. Таковым является, например, обычное математическое равенство (« = »).

Отношение эквивалентности r разбивает множество М на классы эквивалентности: M / r. Между элементами каждого такого класса существует РСТ-отношение. Класс эквивалентности обозначается с использованием квадратных скобок. Внутри указывается любой элемент класса.

Например, широко используемые в теории чисел сравнения задают разбиение множества целых чисел Zна m классов эквивалентности, где m – некоторый модульсравнения: r_m ={(x, y): x – y = k m, m Î N, k Î Z}.

При m=5 получаем: [1]={6, 11, 16, –4, 1, …},

[34]={29, 39, 4, …},

… …

Фактически различных классов эквивалентности здесь всего 5 – столько «простых» вычетовпо модулю 5. Эти вычеты (остатки от деления на 5): 0, 1, 2, 3, 4.

[0] = {… , –5, 0, 5, 10, …},

[1] = {… , –4, 1, 6, 11, …},

… …

[4] = {… , –1, 4, 9, 14, …}.

Кстати, сами сравнения записываются в виде:

0 º 5 (mod 5),

1 º –4 (mod 5),

… …

Они обладают многими свойствами, аналогичными свойствам обычных равенств. Но это уже специальная тема.

Отношение порядка

Это второе «замечательное» отношение (в математическом анализе есть второй замечательный предел, определяющий константу e = 2,71828…: ).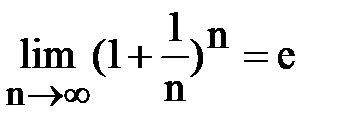

Частичный порядок на множестве M – это любое рефлексивное, транзитивное и антисимметричное (РТА-) отношение. В обычной математике ему соответствует отношение нестрогого неравенства « £ ».

Наиболее важное свойство отношения порядка – его транзитивность.

Кстати, отношение £ и < (строгое неравенство) связаны очень просто:

а < b Û а £ b и а ¹ b, а £ b Û а < b или а = b.

Видно, что отношение строгого порядка нерефлексивно.

Полное отношение порядка r на M означает, что для любых элементов x, y Î M выполняется xry и/или yrx, причем r – это РТА- отношение.

В связи c упорядочиванием элементов вводится множество таких понятий:

–верхняя граница элементовx, y (u Î M, x £ u, y £ u);

– нижняя граница элементов x, y (v Î M, v £ x, v £ y);

–верхняя грань элементов x, y («супремум»); m Î M, m £ _"u; здесь верхних границ u – множество; m = sup (x, y));

– нижняя грань элементов x, y («инфимум»; n Î M, _"v £ n; n = inf (x, y));

– замкнутый интервал значений ([a, b] = {x : x Î R, a £ x £ b } );

–открытый интервал ( ] a, b [ = { x : x Î R, a < x < b} );

–полуоткрытый интервал ( ] a, b ] = { x : x Î R, a < x £ b} или [ a, b [ = {x : x Î R,

a £ x < b} );

–концевые точки интервала (a, b).