Размещение, перестановки и сочетания с повторениями.
Определение: Пусть нам заданы два параметра n и k, взятые из множества N0. Размещением с повторениями из n элементов множества В, В={b1, b2,…, bn} по k элементам будем называть всякую последовательность длины k, составленную из элементов этого множества (среди элементов возможны повторения).
Пример: Пусть нам дано множество С={а, b, с}. Выпишем все размещения с повторениями из 3 элементов по 2 элемента.
 ={(а,а), (b,b), (с,с), (a,b), (a,c), (b,c), (b,a), (c,a), (c,b)}.
={(а,а), (b,b), (с,с), (a,b), (a,c), (b,c), (b,a), (c,a), (c,b)}.
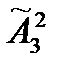 =9
=9
Теоремаn, kÎN0, В={b1, b2,…, bn}. Число размещений из n элементов по k элементам может быть рассчитано по формуле:
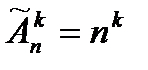 .
.
Определение: Пусть nÎN0, В={b1, b2,…, bn}. Перестановкой с повторениями из элементов множества В называется всякое размещение с повторениями длины n.
Пусть k1, k2,…, km – целые неотрицательные числа, такие, что их сумма k1+k2+…+km=n. Число перестановок с повторениями в которых m различных элементов множества В и ki элементов i-го вида ( 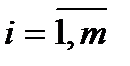 ) будем обозначать Рn(k1, k2, …,km) и называть полиномиальными коэффициентами.
) будем обозначать Рn(k1, k2, …,km) и называть полиномиальными коэффициентами.
Пример: Дано множество А, содержащее элементы А={а, b, с, d}. Выпишем все перестановки с повторениями, в которых содержится 1 элемент а и 3 элемента b.
k1=1
k2=3 n= k1+k2=4 (a,b,b,b), (b,a,b,b) (b,b,a,b) (b,b,b,a)
P4(1,3)
ТеоремаПусть nÎN0, В={b1, b2,…, bn}, ki – целое неотрицательное число, такие, что 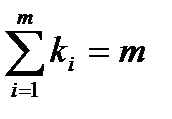 ,тогдачисло перестановок с повторениями можно рассчитать по формуле: Рn(k1, k2, …,km)=
,тогдачисло перестановок с повторениями можно рассчитать по формуле: Рn(k1, k2, …,km)= 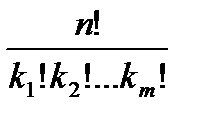
Задача: Для запирания сейфов и автоматических камер хранения применяют секретные замки, которые открываются лишь тогда, когда набрано некоторое тайное слово. Это слово набирают с помощью одного или нескольких дисков на которых помещены буквы или цифры. Пусть на диск помещены 12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком не знающим секретное слово.
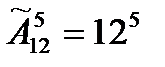 lнеуд=125-1=248831
lнеуд=125-1=248831
Задача: Сколько различных слов можно составить переставляя буквы слова «математика»
n=10
A k1=3
М k2=2 Р10(3,2,2,1,1,1)= 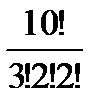 =151200
=151200
Т k3=2
Определение: Пусть параметр k принадлежит множеству N0, параметр n принадлежит N, сочетаниемиз n элементов по k элементамс повторениями называется совокупность, содержащая k элементов, причем каждый элемент принадлежит к одному из n типов.
Пусть дано множество, состоящее из трех букв В={а, b, с}, составим все сочетания с повторениями из трех заданных букв по 2
n=3 k=2 {а, a}, {b, b}, {c, с}, {а, b}, {а, с},{b, с} 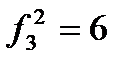
1100 0110 0011 1010 1001 0101 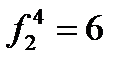
ТеоремаПусть kÎN0, nÎN, число сочетаний с повторениями: 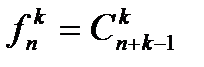 (*)
(*)
выбирая некоторый элемет из n каждый раз дополняем множество точно таким же, всего таких дополнений k-1. фактически, выбор делаем из n+k-1 элемента.
Задача: Сколько было бы костей домино, если на костях могут присутствовать а) 11 значков, б)7 значков
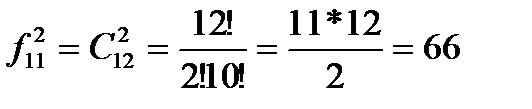
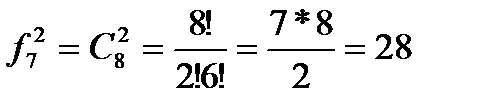
Дата добавления: 2017-08-01; просмотров: 1218;
