Первая теорема двойственности
Теоремы двойственности позволяют установить связь между оптимальными решениями пары двойственных задач. Решив одну из пары двойственных задач, можно или найти оптимальное решение другой задачи, не решая ее, или установить его отсутствие. Возможны следующие случаи: 1) обе задачи из пары двойственных имеют оптимальные решения; 2) одна из задач не имеет решения ввиду неограниченности целевой функции, а другая не имеет решения ввиду несовместности системы ограничений; 3) обе задачи из пары двойственных не имеют решений из-за неограниченности целевых функций.
Теорема 5.1. Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение; причем значения целевых функций задач на своих оптимальных решениях совпадают. Если же одна из пары двойственных задач не имеет решения ввиду неограниченности целевой функции, то другая не имеет решения ввиду несовместности системы ограничений.
Доказательство. Пусть имеется несимметричная пара двойственных задач
Z(X) = CX  max,
max, 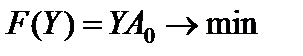 ,
,
AX = 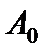 ,
, 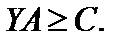
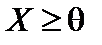 .
.
Прежде, чем приступить к доказательству, получим ряд соотношений. Предположим, что первая (прямая) из задач решалась симплексным методом и получено оптимальное решение 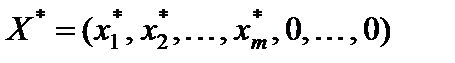 с базисом
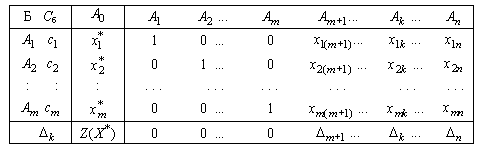
с базисом 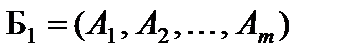 . Запишем последнюю симплексную таблицу (табл. 5.1).
. Запишем последнюю симплексную таблицу (табл. 5.1).
Т а б л и ц а 5.1
Запишем разложение вектора 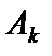 по базису оптимального решения
по базису оптимального решения
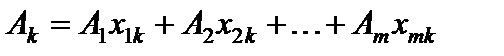 , k = 0, 1, 2, . . . , n.
, k = 0, 1, 2, . . . , n.
Преобразуем данное разложение
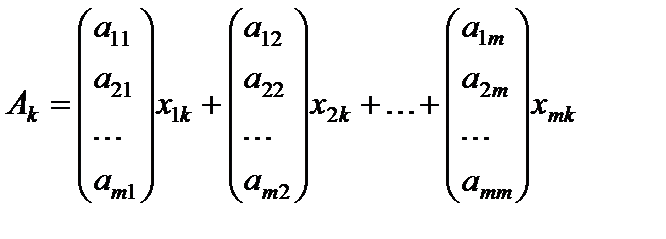 =
=
= 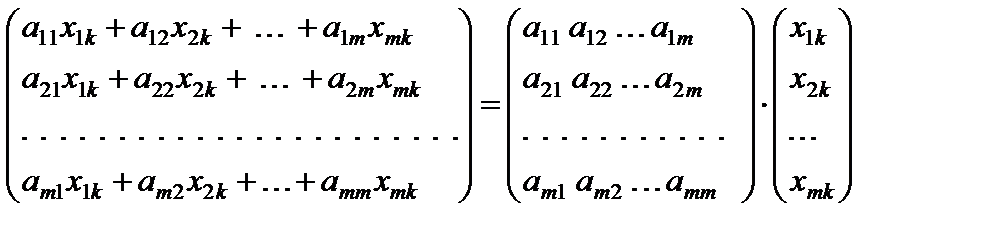 ,
,
k = 0, 1, 2, ..., n.
Обозначим
D = 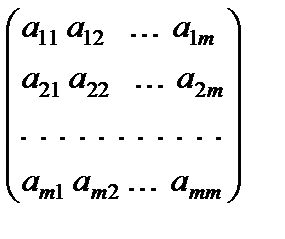 ,
, 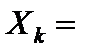
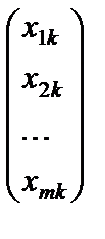 ,
,
тогда
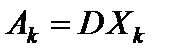 , k = 0, 1, 2, ..., n. (5.11)
, k = 0, 1, 2, ..., n. (5.11)
Умножим данное матричное равенство на обратную матрицу 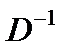 слева:
слева:
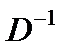
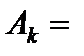
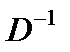 D
D 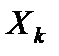 .
.
Так как 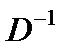 D = Е, Е
D = Е, Е 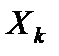 =
= 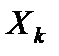 ,то
,то
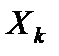 =
= 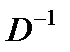
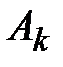 , k = 0, 1, 2, ..., n. (5.12)
, k = 0, 1, 2, ..., n. (5.12)
Аналогично можно получить
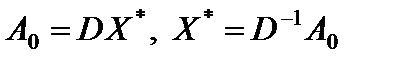 . (5.13)
. (5.13)
Запишем с учетом полученного оценки 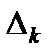 , k = 0, 1, 2, ..., n.
, k = 0, 1, 2, ..., n.
В общем случае формула для расчета оценок имеет вид (4.9)
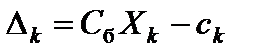 .
.
Обозначим через С* матрицу-строку коэффициентов при базисных переменных в оптимальном решении. Тогда для оценок разложений векторов-условий по базису оптимального решения имеем
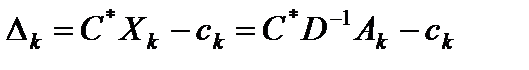 . (5.14)
. (5.14)
Обозначим матрицу, составленную из векторов 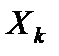 через
через 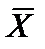 , т. е.
, т. е.  ; матрицу-строку из оценок
; матрицу-строку из оценок 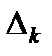 через
через  , т. е.
, т. е. 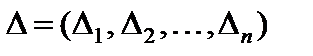 и матрицу-строку коэффициентов целевой функции через С, т. е.
и матрицу-строку коэффициентов целевой функции через С, т. е. 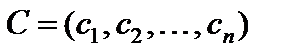 . Кроме того, матрица системы уравнений-ограничений
. Кроме того, матрица системы уравнений-ограничений 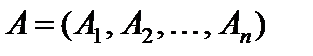 ,тогда из формул (5.12) и (5.14) следует
,тогда из формул (5.12) и (5.14) следует
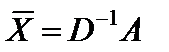 , (5.15)
, (5.15)
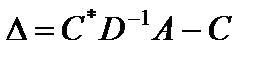 . (5.16)
. (5.16)
Теперь приступим к доказательству первого утверждения теоремы.
1. Докажем, что допустимое решение двойственной задачи имеет вид
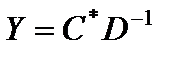 . (5.17)
. (5.17)
Поскольку решение прямой задачи 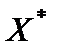 на максимум оптимальное, то ее оценки неотрицательные
на максимум оптимальное, то ее оценки неотрицательные
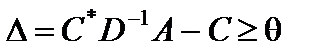 .
.
Отсюда
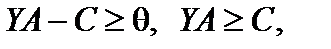
т. е. 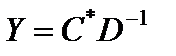 удовлетворяет системе ограничений двойственной задачи.
удовлетворяет системе ограничений двойственной задачи.
2. Докажем, что при 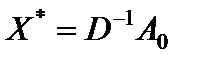 и
и 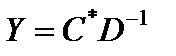
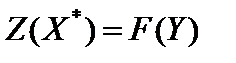 . (5.18)
. (5.18)
Получаем

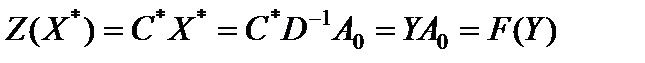 .
.
3. Докажем, что
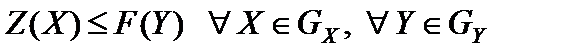 , (5.19)
, (5.19)
где 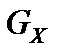 - область допустимых решений прямой задачи;
- область допустимых решений прямой задачи; 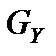 - область допустимых решений двойственной задачи.
- область допустимых решений двойственной задачи.
Для этого систему ограничений прямой задачи умножим слева на допустимое решение двойственной задачи Y, а систему ограничений двойственной задачи умножим справа на допустимое решение Х исходной задачи, получим
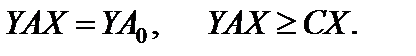
Так как  то
то
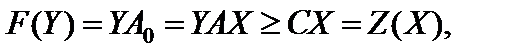
т. е. 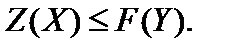
4. Далее докажем, что 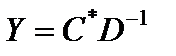 является оптимальным решением. Так как прямая задача на максимум, а
является оптимальным решением. Так как прямая задача на максимум, а 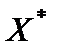 – оптимальное решение, то
– оптимальное решение, то 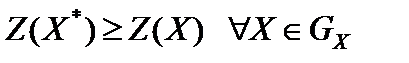 . Двойственная задача на минимум, поэтому значение ее целевой функции на оптимальном решении
. Двойственная задача на минимум, поэтому значение ее целевой функции на оптимальном решении 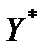 должно удовлетворять условию
должно удовлетворять условию 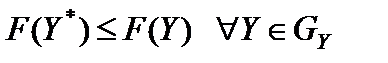 . Как показано в пункте 3,
. Как показано в пункте 3, 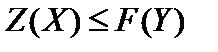
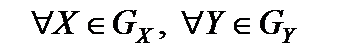 , поэтому значение
, поэтому значение  не может быть меньше
не может быть меньше 
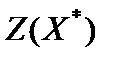 , а может быть только равно
, а может быть только равно 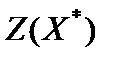 . Это равенство достигается при
. Это равенство достигается при  , которое и будет оптимальным решением двойственной задачи. Первое утверждение теоремы доказано.
, которое и будет оптимальным решением двойственной задачи. Первое утверждение теоремы доказано.
Запишем полезное соотношение для нахождения оптимального решения двойственной задачи. Матричное равенство 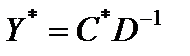 представим следующим образом:
представим следующим образом:
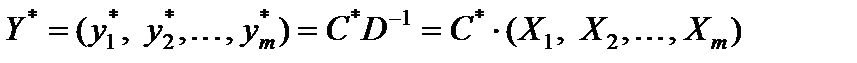 ,
,
где 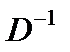 – матрица обратная к матрице D, составленной из векторов-условий задачи, образующих базис оптимального решения. Матрица
– матрица обратная к матрице D, составленной из векторов-условий задачи, образующих базис оптимального решения. Матрица 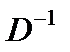 находится в последней симплексной таблице под единичными векторами первой симплексной таблицы.
находится в последней симплексной таблице под единичными векторами первой симплексной таблицы.
Отсюда следует, что 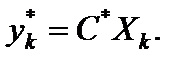 Так как
Так как 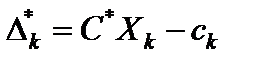 , то
, то 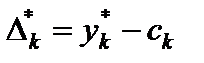 или
или
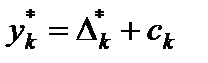 . (5.20)
. (5.20)
Данная формула позволяет, используя оценки последней симплексной таблицы решения прямой задачи, записывать оптимальное решение двойственной задачи как сумму оценок и коэффициентов целевой функции.
Докажем второе утверждение теоремы. Пусть прямая задача не имеет оптимального решения ввиду неограниченности целевой функции Z(X) ® +¥. Так как  и
и 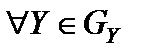 , то или
, то или 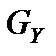 является пустым множеством, или
является пустым множеством, или  .
.
Пример 5.3. Для данной задачи составить двойственную, решить ее симплексным методом и, используя первую теорему двойственности, найти решение исходной задачи:

Решение. Используя вторую симметричную пару двойственных задач (5.8), составляем задачу, двойственную к исходной.
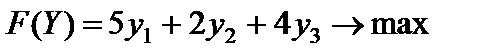 ,
,
| Д |

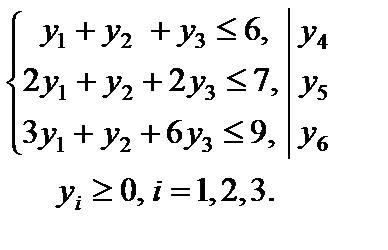
Вводим неотрицательные дополнительные переменные  для приведения задачи к каноническому виду, получаем
для приведения задачи к каноническому виду, получаем
Т а б л и ц а 5.2
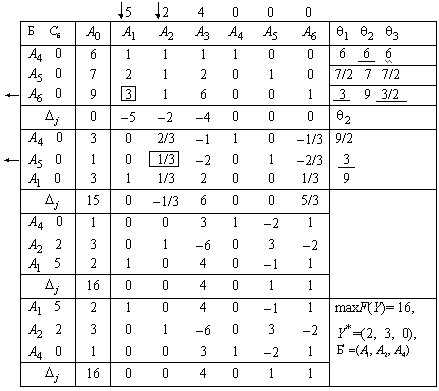
Находим начальное опорное решение 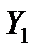 = (0, 0, 0, 6, 7, 9) с единичным базисом
= (0, 0, 0, 6, 7, 9) с единичным базисом 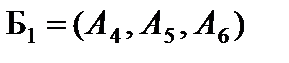 . Решение задачи симплексным методом приведено в табл. 5.2.
. Решение задачи симплексным методом приведено в табл. 5.2.
Оптимальное решение двойственной задачи 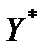 = (2, 3, 0), его базис
= (2, 3, 0), его базис 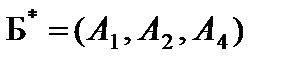 , значение целевой функции
, значение целевой функции
max F(Y) = F( 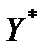 ) = 16. Оптимальное решение исходной задачи, двойственной к решенной, найдем по формуле (5.17)
) = 16. Оптимальное решение исходной задачи, двойственной к решенной, найдем по формуле (5.17)

Матрица D состоит из координат векторов 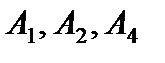 , входящих в базис оптимального решения двойственной задачи
, входящих в базис оптимального решения двойственной задачи

Матрица 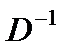 находится в последней симплексной таблице. Ее столбцы располагаются под столбцами единичной матрицы, т. е. под единичными векторами
находится в последней симплексной таблице. Ее столбцы располагаются под столбцами единичной матрицы, т. е. под единичными векторами 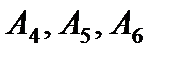 , образующими базис начального опорного решения:
, образующими базис начального опорного решения:
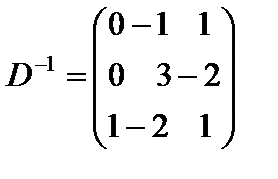 .
.
Координатами вектора 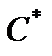 являются коэффициенты целевой функции при базисных неизвестных оптимального решения
являются коэффициенты целевой функции при базисных неизвестных оптимального решения  . Данные коэффициенты записываются в том же порядке, в каком векторы условий входят в базис оптимального решения, т. е.
. Данные коэффициенты записываются в том же порядке, в каком векторы условий входят в базис оптимального решения, т. е.  (5, 2, 0).
(5, 2, 0).
Вычисляем
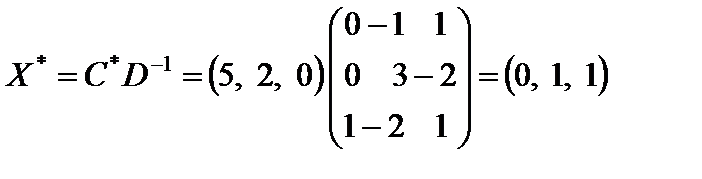 .
.
Оптимальное решение исходной задачи можно найти проще по формуле (5.20)
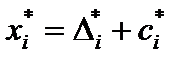 , i = 1, 2, 3.
, i = 1, 2, 3.
Для этого необходимо к оценкам разложений векторов  , входящих в базис начального опорного решения по базису оптимального решения, т. е. к оценкам этих векторов в последней симплексной таблице, прибавить соответствующие коэффициенты целевой функции (в таблице они расположены в верхней строке над оценками)
, входящих в базис начального опорного решения по базису оптимального решения, т. е. к оценкам этих векторов в последней симплексной таблице, прибавить соответствующие коэффициенты целевой функции (в таблице они расположены в верхней строке над оценками)
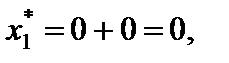
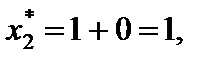

Ответ: min Z(X) = 16 при 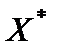 = (0, 1, 1).
= (0, 1, 1).
Пример 5.4. Найти решение данной задачи и двойственной к ней.

Решение. Задача, двойственная к данной, имеет вид
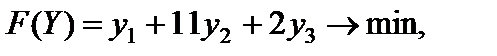
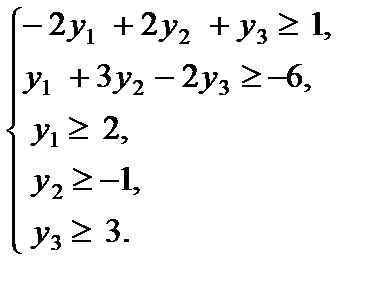
В данной паре двойственных задач легче решить исходную задачу, так как она имеет начальное опорное решение 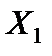 = (0, 0, 1, 11, 2) с единичным базисом
= (0, 0, 1, 11, 2) с единичным базисом 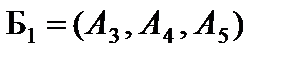 и ее без дополнительных преобразований можно решить симплексным методом. Решение исходной задачи приведено в табл. 5.3.
и ее без дополнительных преобразований можно решить симплексным методом. Решение исходной задачи приведено в табл. 5.3.
Т а б л и ц а 5.3
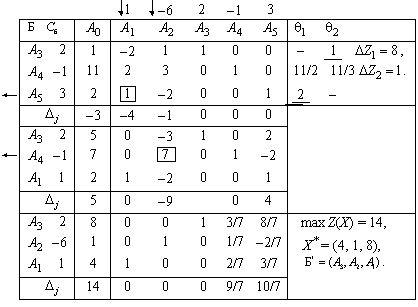
Оптимальным решением исходной задачи является вектор
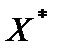 = (4, 1, 8), базис оптимального решения
= (4, 1, 8), базис оптимального решения 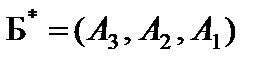 , значение целевой функции
, значение целевой функции 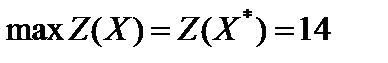 . По формуле (5.17) находим оптимальное решение двойственной задачи
. По формуле (5.17) находим оптимальное решение двойственной задачи
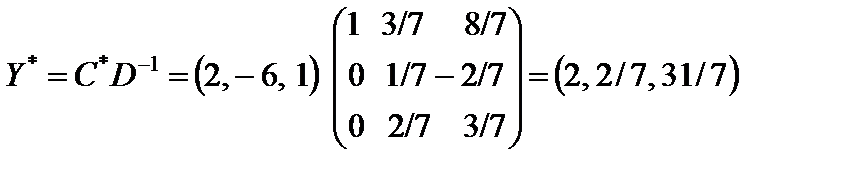 .
.
Данное решение можно найти также по формулам (5.20) 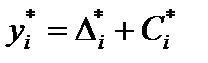 :
:
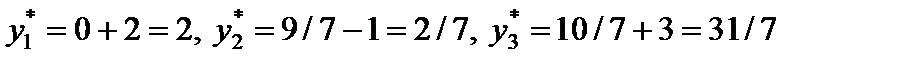 .
.
Таким образом, оптимальным решением двойственной задачи является вектор 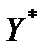 = (2, 2/7, 31/7), min F(Y) = F(
= (2, 2/7, 31/7), min F(Y) = F( 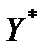 ) = 14.
) = 14.
Ответ: max Z(X)=14 при 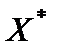 =(4, 1, 8); min F(Y) =14 при
=(4, 1, 8); min F(Y) =14 при 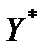 =(2, 2/7, 31/7).
=(2, 2/7, 31/7).
Дата добавления: 2017-05-18; просмотров: 1307;
