Особенности алгоритма метода искусственного базиса
Алгоритм метода искусственного базиса имеет следующие особенности:
1. Ввиду того, что начальное опорное решение расширенной задачи содержит искусственные переменные, входящие в целевую функцию с коэффициентом -М (в задаче на максимум) или +М (в задаче на минимум), оценки разложений векторов условий 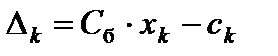 состоят из двух слагаемых
состоят из двух слагаемых 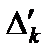 и
и 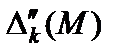 , одно из которых
, одно из которых 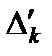 не зависит от М, а другое
не зависит от М, а другое 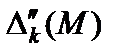 зависит от М. Так как М скольугодно велико по сравнению с единицей (М>>1), то на первом этапе расчета для нахождения векторов, вводимых в базис, используются только слагаемые оценок
зависит от М. Так как М скольугодно велико по сравнению с единицей (М>>1), то на первом этапе расчета для нахождения векторов, вводимых в базис, используются только слагаемые оценок 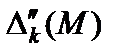 .
.
2. Векторы, соответствующие искусственным переменным, которые выводятся из базиса опорного решения, исключаются из рассмотрения.
3. После того, как все векторы, соответствующие искусственным переменным, исключаются из базиса, расчет продолжается обычным симплексным методом с использованием оценок 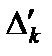 , не зависящих от М.
, не зависящих от М.
4. Переход от решения расширенной задачи к решению исходной задачи производится с использованием доказанных выше теорем 4.1-4.3.
Пример 4.4. Решить задачу линейного программирования методом искусственного базиса
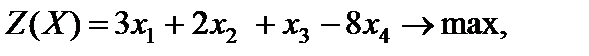
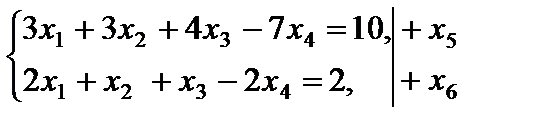
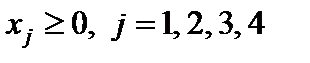 .
.
Решение. Составляем расширенную задачу. В левые части уравнений системы ограничений вводим неотрицательные искусственные переменные с коэффициентом (всегда) +1. Удобно справа от уравнений записать вводимые искусственные переменные. В первое уравнение вводим 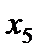 , во второе -
, во второе - 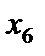 . Данная задача - задача на нахождение максимума, поэтому
. Данная задача - задача на нахождение максимума, поэтому 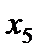 и
и 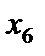 в целевую функцию вводятся с коэффициентом - М. Получаем
в целевую функцию вводятся с коэффициентом - М. Получаем
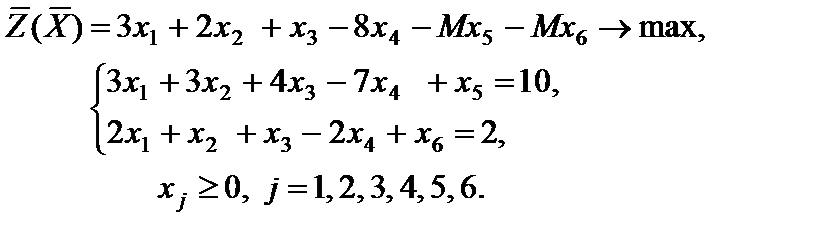
Задача имеет начальное опорное решение 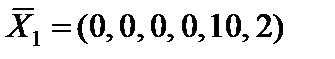 с единичным базисом
с единичным базисом 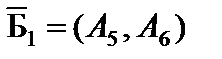 . Вычисляем оценки векторов условий по базису опорного решения и значение целевой функции на опорном решении.
. Вычисляем оценки векторов условий по базису опорного решения и значение целевой функции на опорном решении.
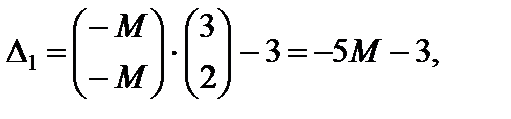
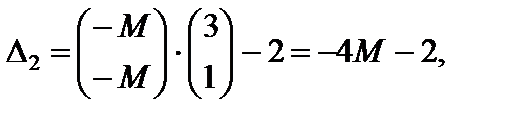
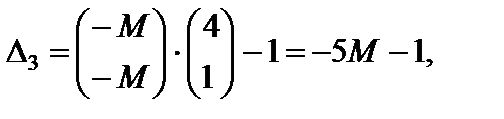
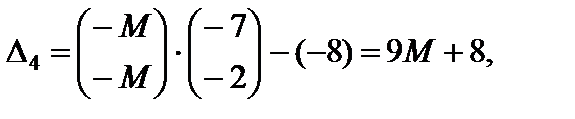
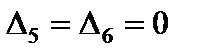 .
. 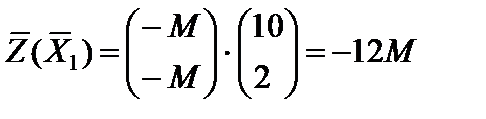 .
.
Записываем исходные данные в симплексную таблицу (табл. 4.6).
Т а б л и ц а 4.6
При этом оценки 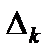 и
и 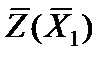 для удобства вычислений записываем в две строки: в первую - слагаемые
для удобства вычислений записываем в две строки: в первую - слагаемые 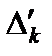 , не зависящие от М, во вторую - слагаемые
, не зависящие от М, во вторую - слагаемые 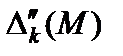 , зависящие от М. Значения
, зависящие от М. Значения 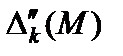 удобно указывать без М, имея в виду однако, что оно там присутствует.
удобно указывать без М, имея в виду однако, что оно там присутствует.
Начальное опорное решение не является оптимальным, так как в задаче на максимум имеются отрицательные оценки. Выбираем номер вектора 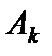 , вводимого в базис опорного решения, и номер вектора
, вводимого в базис опорного решения, и номер вектора 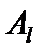 , выводимого из базиса. Для этого вычисляем приращения целевой функции
, выводимого из базиса. Для этого вычисляем приращения целевой функции 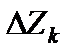 при введении в базис каждого из векторов с отрицательной оценкой и находим максимум этого приращения. При этом слагаемыми оценок
при введении в базис каждого из векторов с отрицательной оценкой и находим максимум этого приращения. При этом слагаемыми оценок 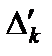 (без М) пренебрегаем до тех пор, пока хотя бы одно слагаемое
(без М) пренебрегаем до тех пор, пока хотя бы одно слагаемое 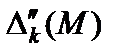 (с М) не будет отлично от нуля. В связи с этим строка со слагаемыми оценок
(с М) не будет отлично от нуля. В связи с этим строка со слагаемыми оценок 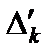 может отсутствовать в таблице до тех пор, пока присутствует строка
может отсутствовать в таблице до тех пор, пока присутствует строка 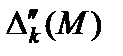 . Находим
. Находим 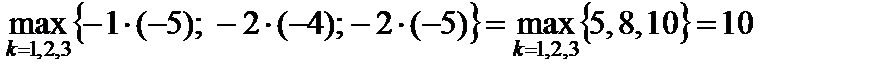 при k = 3.
при k = 3.
В третьем столбце " 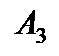 " за разрешающий элемент выбираем коэффициент 1 во второй строке и выполняем преобразование Жордана.
" за разрешающий элемент выбираем коэффициент 1 во второй строке и выполняем преобразование Жордана.
Вектор 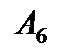 , выводимый из базиса, исключаем из рассмотрения (вычеркиваем). Получаем опорное решение
, выводимый из базиса, исключаем из рассмотрения (вычеркиваем). Получаем опорное решение 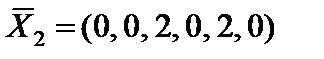 с базисом
с базисом 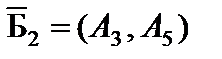 (табл. 4.7). Решение не является оптимальным так как имеется отрицательная оценка
(табл. 4.7). Решение не является оптимальным так как имеется отрицательная оценка 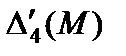 = -1.
= -1.
Т а б л и ц а 4.7
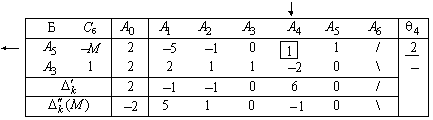
В столбце " 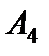 " единственный положительный элемент принимаем за разрешающий и переходим к новому опорному решению
" единственный положительный элемент принимаем за разрешающий и переходим к новому опорному решению 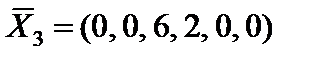 с базисом
с базисом 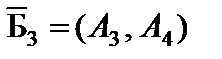 (табл. 4.8).
(табл. 4.8).
Т а б л и ц а 4.8
Данное опорное решение является единственным оптимальным решением расширенной задачи, так как в задаче на максимум оценки для всех векторов, не входящих в базис, положительны. По теореме 4.1 исходная задача также имеет оптимальное решение, которое получается из оптимального решения расширенной задачи отбрасыванием нулевых искусственных переменных, т. е. Х* = (0,0,6,2).
Ответ: max Z(X) = -10 при 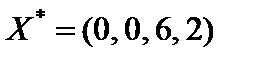 .
.
Пример 4.5. Решить методом искусственного базиса задачу линейного программирования со смешанными ограничениями
| Д И |
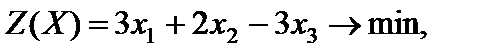
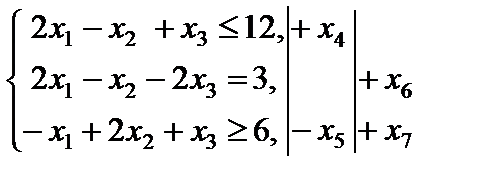
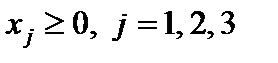
Решение. Приводим задачу линейного программирования к каноническому виду. Для этого вводим дополнительные переменные 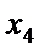 и
и 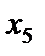 в первое и третье ограничения соответственно. Получаем
в первое и третье ограничения соответственно. Получаем
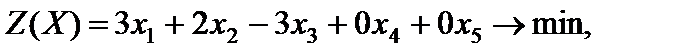
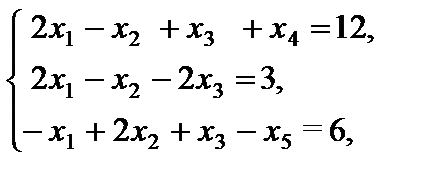
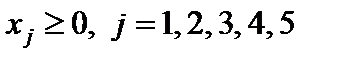 .
.
Составляем расширенную задачу, для чего вводим искусственные переменные 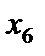 и
и 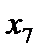 во второе и третье уравнения соответственно. Получаем
во второе и третье уравнения соответственно. Получаем
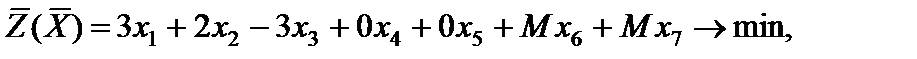
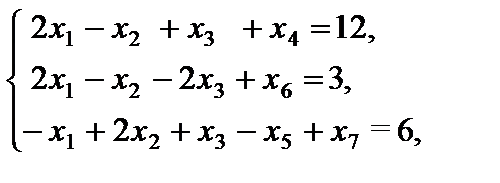
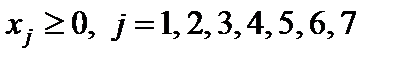 .
.
Данная расширенная задача имеет начальное опорное решение
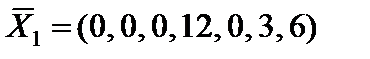 с единичным базисом
с единичным базисом 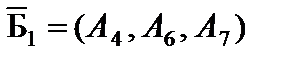 ,
, 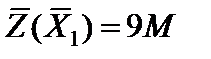 . Вычисляем оценки векторов условий по базису опорного решения и записываем в симплексную таблицу так же, как в предыдущем примере. Решение
. Вычисляем оценки векторов условий по базису опорного решения и записываем в симплексную таблицу так же, как в предыдущем примере. Решение 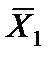 не является оптимальным, так как в задаче на минимум векторы
не является оптимальным, так как в задаче на минимум векторы 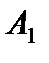 и
и 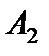 имеют положительные оценки
имеют положительные оценки 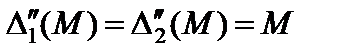 . Улучшаем опорные решения. Каждому опорному решению соответствует своя таблица. Все таблицы можно записать друг под другом, объединив в единую таблицу (табл. 4.9).
. Улучшаем опорные решения. Каждому опорному решению соответствует своя таблица. Все таблицы можно записать друг под другом, объединив в единую таблицу (табл. 4.9).
Т а б л и ц а 4.9
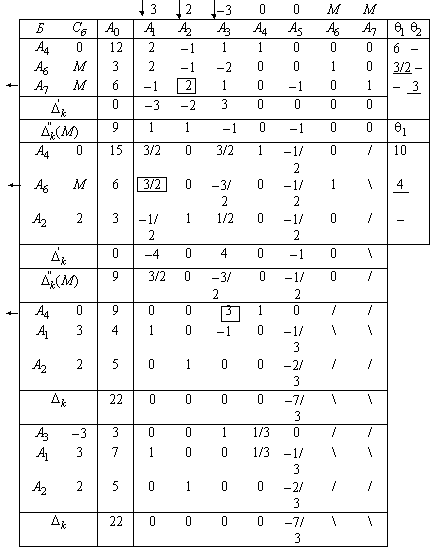
Определяем, введение какого из векторов 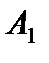 или
или 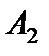 в базис начального опорного решения приведет к большему уменьшению целевой функции. Находим
в базис начального опорного решения приведет к большему уменьшению целевой функции. Находим 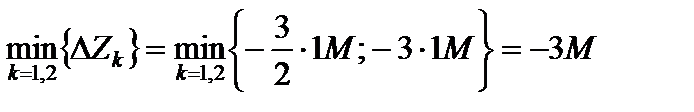 при k = 2, т. е. лучше ввести в базис вектор
при k = 2, т. е. лучше ввести в базис вектор 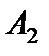 . Получаем второе опорное решение
. Получаем второе опорное решение 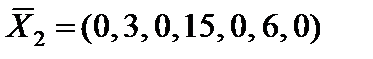 с базисом
с базисом 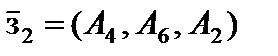 . Целевая функция
. Целевая функция 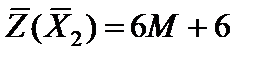 . Это решение также не является оптимальным, так как вектор
. Это решение также не является оптимальным, так как вектор 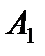 имеет положительную оценку
имеет положительную оценку 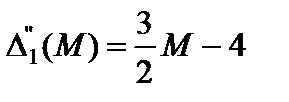 . Вводим вектор
. Вводим вектор 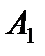 в базис, получаем третье опорное решение
в базис, получаем третье опорное решение 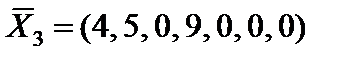 с базисом
с базисом 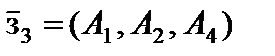 . Целевая функция
. Целевая функция 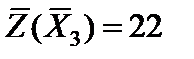 . Это решение оптимальное, но не единственное, так как вектор
. Это решение оптимальное, но не единственное, так как вектор 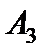 , не входящий в базис, имеет нулевую оценку. Поэтому необходимо перейти к новому опорному решению, которое также будет оптимальным. Для этого требуется ввести в базис вектор
, не входящий в базис, имеет нулевую оценку. Поэтому необходимо перейти к новому опорному решению, которое также будет оптимальным. Для этого требуется ввести в базис вектор 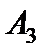 .
.
Переходим к четвертому опорному (оптимальному) решению
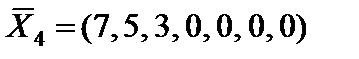 с базисом
с базисом 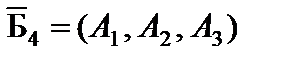 , при этом
, при этом 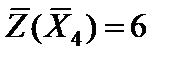 . Оптимальные решения расширенной задачи
. Оптимальные решения расширенной задачи 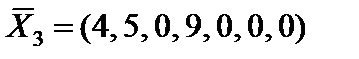 ,
, 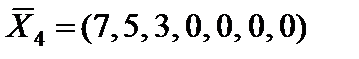 имеют нулевые искусственные переменные. Поэтому (по теореме 4.1) исходная задача также имеет два оптимальных решения
имеют нулевые искусственные переменные. Поэтому (по теореме 4.1) исходная задача также имеет два оптимальных решения 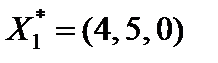 и
и 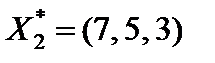 . Дополнительные переменные
. Дополнительные переменные 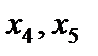 в оптимальном решении исходной задачи не записываем.
в оптимальном решении исходной задачи не записываем.
Ответ: 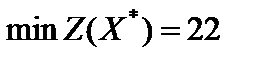 при
при 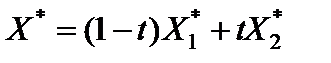 ,
, 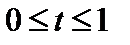 ,
, 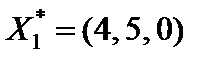 ,
, 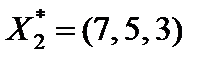 .
.
Дата добавления: 2017-05-18; просмотров: 911;
