Пример 4.3. Решить симплексным методом задачу

,

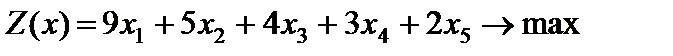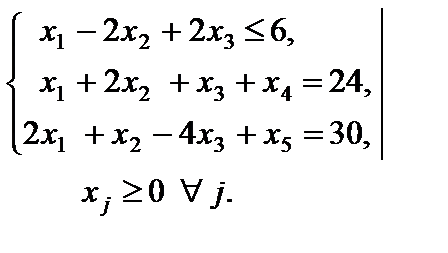
Решение. Приводим задачу к каноническому виду. Для этого в левую часть первого ограничения неравенства типа " £ " вводим дополнительную переменную 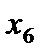с коэффициентом +1. В целевую функцию переменная 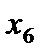входит с коэффициентом 0 (т. е. не входит). Получаем

,

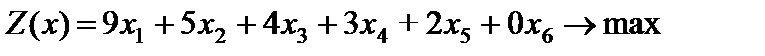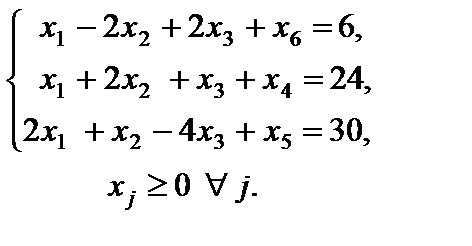
Находим начальное опорное решение. Для этого свободные (неразрешенные) переменные приравниваем к нулю 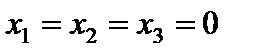. Получаем опорное решение 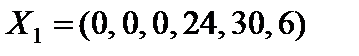с единичным базисом .

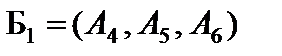Вычисляем оценки разложений векторов условий по базису опорного решения по формуле (4.9).

;

;

;

;

;

.

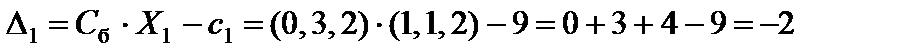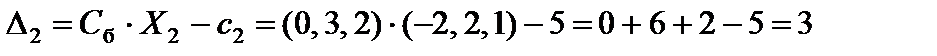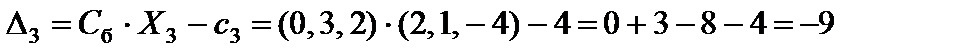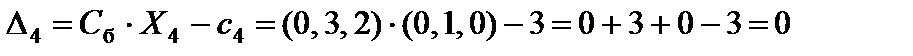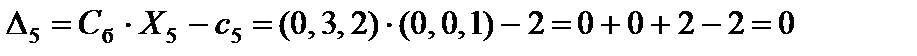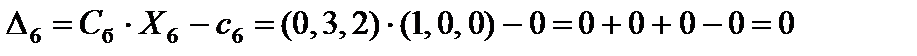Оценки векторов, входящих в базис, всегда равны нулю. Обычно эти вычисления производятся устно. Опорное решение, коэффициенты разложений и оценки разложений векторов условий по базису опорного решения записываются в симплексную таблицу (табл. 4.3).

Т а б л и ц а 4.3

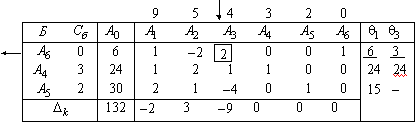
Сверху над таблицей для удобства вычислений оценок записываются коэффициенты целевой функции. В первом столбце "Б" записываются векторы, входящие в базис опорного решения. Порядок записи этих векторов соответствует номерам разрешенных неизвестных в уравнениях – ограничениях. Во втором столбце таблицы " 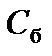" – коэффициенты целевой функции при базисных переменных в том же порядке. При правильном расположении коэффициентов целевой функции в столбце " 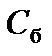" оценки единичных векторов, входящих в базис, всегда равны нулю.

В последней строке таблицы с оценками 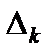в столбце " 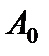" записывается значение целевой функции на опорном решении .

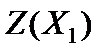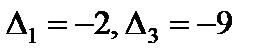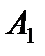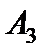Начальное опорное решение не является оптимальным, так как в задаче на максимум оценки для векторов и противоречат признаку оптимальности. Для оптимальности опорного решения в задаче на максимум требуется неотрицательность оценок для всех векторов условий.

По теореме об улучшении опорного решения, если в задаче на максимум хотя бы один вектор имеет отрицательную оценку, то можно найти новое опорное решение, на котором значение целевой функции будет больше. Определим, введение какого из двух векторов приведет к большему приращению целевой функции. Приращение целевой функции находится по формуле 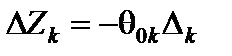. Вычисляем значения параметра 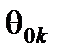для первого и третьего столбцов по формуле (4.5), получаем 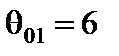при l = 1; 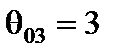при l = 1 (табл. 4.3). Находим приращение целевой функции при введении в базис первого вектора 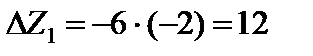и третьего вектора 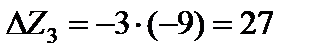. Следовательно, для более быстрого приближения к оптимальному решению необходимо ввести в базис опорного решения вектор 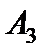вместо первого вектора базиса 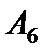, так как минимум параметра 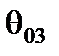достигается в первой строке (l = 1). Производим преобразование Жордана с элементом 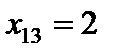, получаем второе опорное решение 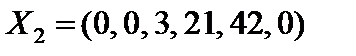с базисом 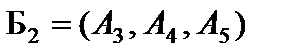(табл. 4.4). Это решение не является оптимальным, так как вектор 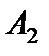имеет отрицательную оценку 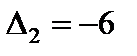. Для улучшения решения необходимо ввести вектор 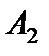в базис опорного решения.

Т а б л и ц а 4.4

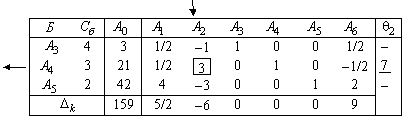
Определяем номер вектора, выводимого из базиса. Для этого вычисляем параметр 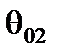для второго столбца, он равен 7 при l = 2. Следовательно, из базиса выводим второй вектор базиса 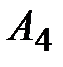. Производим преобразование Жордана с элементом 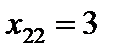, получаем третье опорное решение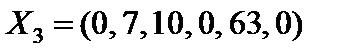 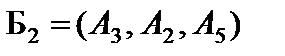(табл. 4.5). Это решение является единственным оптимальным, так как для всех векторов, не входящих в базис, оценки разложений по базису опорного решения положительные .

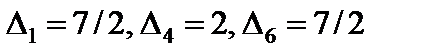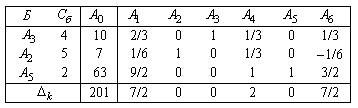
Т а б л и ц а 4.5

Ответ: max Z(X) = 201 при .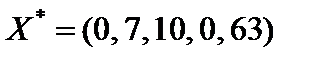

Лекция №7.