Нахождение начального опорного решения и переход к новому опорному решению
Пусть имеется задача линейного программирования в канонической форме
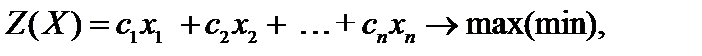 (4.1)
(4.1)
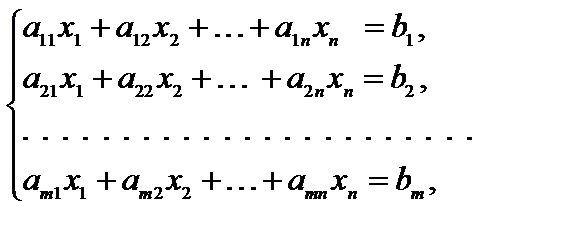 (4.2)
(4.2)
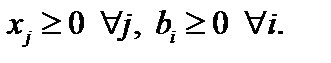 (4.3)
(4.3)
Будем считать, что правые части всех уравнений системы ограничений неотрицательны. Если в каком-либо уравнении правая часть отрицательная, то это уравнение нужно умножить на -1.
Для нахождения опорного решения воспользуемся тем, что любое допустимое базисное решение считается опорным. Найдем базисное решение методом Жордана – Гаусса. При этом разрешающие элементы для всех преобразований Жордана будем выбирать так, чтобы правые части уравнений системы оставались неотрицательными. Тогда полученное базисное решение будет допустимым, т. е. опорным.
Получим правило выбора разрешающих элементов для преобразований Жордана, обеспечивающее сохранение неотрицательности правых частей системы уравнений.
Пусть разрешающим элементом для преобразования Жордана является коэффициент 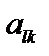 при неизвестной
при неизвестной 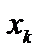 в уравнении с номером l. В результате преобразования Жордана правые части уравнений, как известно, пересчитываются по следующим формулам:
в уравнении с номером l. В результате преобразования Жордана правые части уравнений, как известно, пересчитываются по следующим формулам:
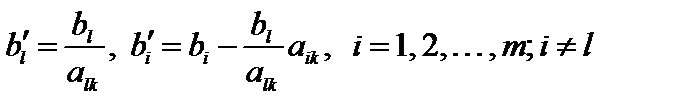 .
.
1. Для того чтобы правая часть 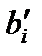 уравнения с разрешающим элементом
уравнения с разрешающим элементом 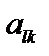 оставалась неотрицательной, должно выполняться неравенство
оставалась неотрицательной, должно выполняться неравенство
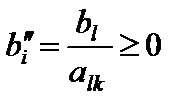 .
.
Так как 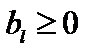 , то первое условие для разрешающего элемента
, то первое условие для разрешающего элемента 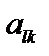 состоит в том, что он должен быть положительным, т. е.
состоит в том, что он должен быть положительным, т. е.
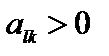 .
.
2. Неотрицательными также должны быть правые части остальных уравнений, т. е.
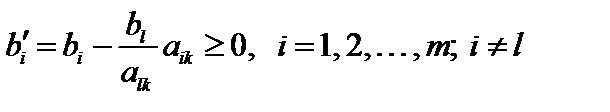 .
.
Для получения требований, налагаемых на разрешающий элемент 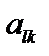 , рассмотрим два случая:
, рассмотрим два случая:
а) если 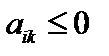 , то ввиду того, что
, то ввиду того, что 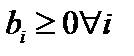 ,
, 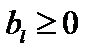 ,
, 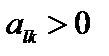 , без дополнительных условий имеем
, без дополнительных условий имеем 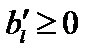 ;
;
б) если же 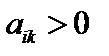 , то неравенство
, то неравенство
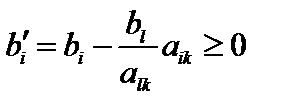
поделим на 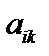 , получим
, получим
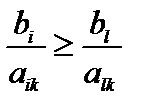 .
.
Данное неравенство должно выполняться для любого уравнения с номером i, в котором 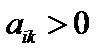 . Для удобства вычислений вводят вспомогательный параметр
. Для удобства вычислений вводят вспомогательный параметр 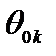
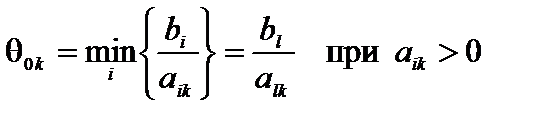 . (4.4)
. (4.4)
где k – номер вектора условия 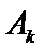 , вводимого в базис (выбираемого столбца матрицы системы ограничений), а l – номер вектора
, вводимого в базис (выбираемого столбца матрицы системы ограничений), а l – номер вектора 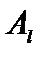 , выводимого из базиса (номер строки матрицы, в которой должен выбираться разрешающий элемент для преобразования Жордана).
, выводимого из базиса (номер строки матрицы, в которой должен выбираться разрешающий элемент для преобразования Жордана).
С помощью данного условия возможно выбрать разрешающий элемент в любом столбце k-матрицы системы ограничений, в котором имеется хотя бы один положительный элемент. При нарушении данного условия выбора разрешающего элемента в правой части системы уравнений появляются отрицательные величины.
Используя данное условие, можно найти начальное опорное решение.
Аналогичное условие может быть использовано при переходе от одного опорного решения к другому.
Пусть система уравнений-ограничений с помощью подходящего выбора разрешающих элементов приведена к равносильной разрешенной так, что правые части системы сохранились неотрицательными, и имеет вид
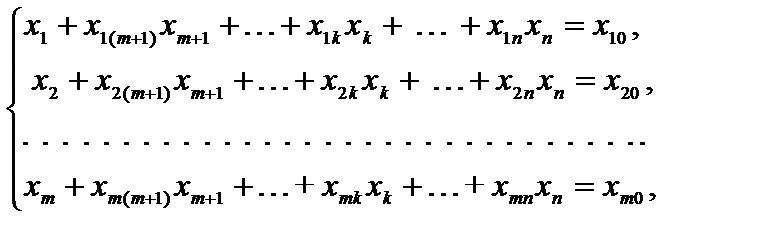
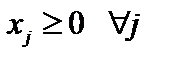 .
.
Тогда базисное решение является допустимым и опорным решением с базисом из единичных векторов 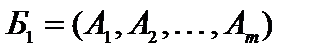 .
.
Очевидно, для перехода от этого опорного решения к новому необходимо использовать соотношение
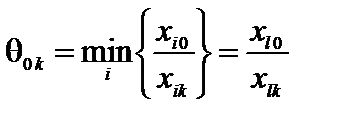 при
при 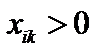 , (4.5)
, (4.5)
где k – номер вектора, вводимого в базис, l – номер вектора, выводимого из базиса, 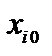 – координаты опорного решения,
– координаты опорного решения, 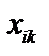 – коэффициенты разложения вектора
– коэффициенты разложения вектора 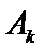 по базису опорного решения.
по базису опорного решения.
Пример 5.1. Найти начальное опорное решение и путем перебора опорных решений найти оптимальное решение задачи
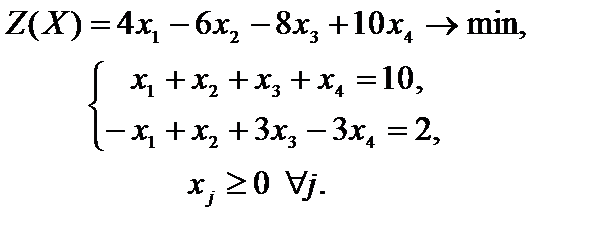
Решение. Результаты нахождения начального опорного решения и дальнейшего перебора опорных решений приведены в табл. 4.1. Справа от таблицы на каждом шаге вычислений приведены значения параметра 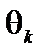 для выбранного столбца k (минимальные значения
для выбранного столбца k (минимальные значения 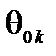 подчеркнуты), соответствующее опорное решение
подчеркнуты), соответствующее опорное решение 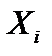 и значение целевой функции
и значение целевой функции 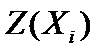 на этом решении. Номера столбцов для выбора разрешающих элементов принимались произвольно.
на этом решении. Номера столбцов для выбора разрешающих элементов принимались произвольно.
Т а б л и ц а 5.1
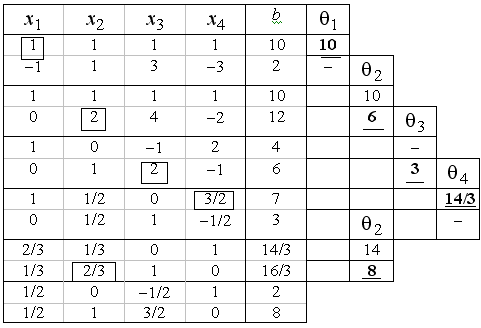
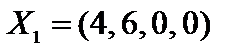 ,
,
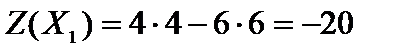 .
.
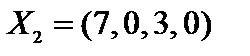 ,
,
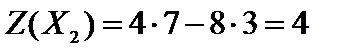 .
.
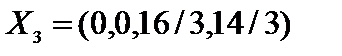 ,
, 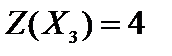 .
.
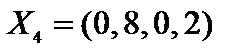 ,
,
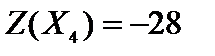 .
.
Сравниваем значения целевой функции на полученных опорных решениях, min{-20, 4, -28} = -28. Находим оптимальное опорное решение
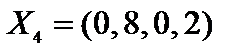 .
.
Ответ: 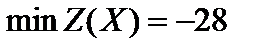 при
при 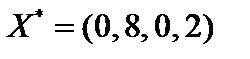 .
.
Данный способ нахождения оптимального решения может вызвать затруднения с перебором всех опорных решений и с завершением процесса решения задачи в случае отсутствия решения, поэтому его следует применять только для приобретения навыков в использовании параметра 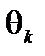 .
.
Дата добавления: 2017-05-18; просмотров: 2034;
