Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками
Рассмотрим систему ограничений некоторой конкретной задачи
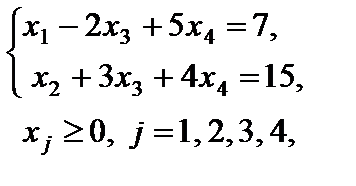 которая в векторной записи имеет вид
которая в векторной записи имеет вид
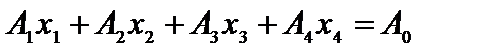 ,
,
где
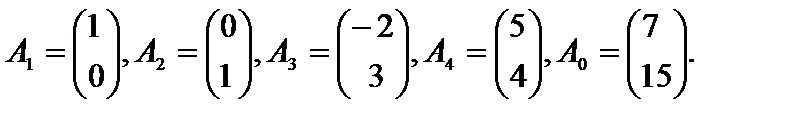
Векторы 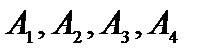 называются векторами условий.
называются векторами условий.
Данная система имеет бесконечное множество допустимых решений, например, 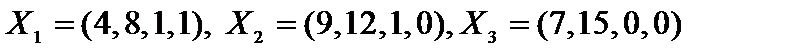 . Вектор
. Вектор 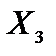 является базисным решением.
является базисным решением.
Положительным координатам допустимых решений ставят в соответствие векторы условий. Для решений 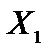 и
и 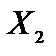 такими будут векторы
такими будут векторы 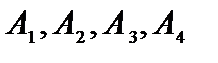 и
и 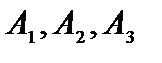 , соответственно. Эти системы векторов являются линейно зависимыми, так как число входящих в них векторов (4 и 3) больше размерности векторов (2). Таких решений бесконечное множество. Для базисного решения
, соответственно. Эти системы векторов являются линейно зависимыми, так как число входящих в них векторов (4 и 3) больше размерности векторов (2). Таких решений бесконечное множество. Для базисного решения 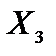 соответствующие положительным координатам единичные векторы
соответствующие положительным координатам единичные векторы 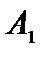 и
и 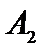 линейно независимые. Как известно, любая система уравнений имеет конечное число базисных решений, равное
линейно независимые. Как известно, любая система уравнений имеет конечное число базисных решений, равное 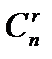 , где n – число неизвестных, r – ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, называются опорными. В дальнейшем будет показано, что они являются угловыми точками области допустимых решений задачи.
, где n – число неизвестных, r – ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, называются опорными. В дальнейшем будет показано, что они являются угловыми точками области допустимых решений задачи.
Опорным решением задачи линейного программирования называется такое допустимое решение 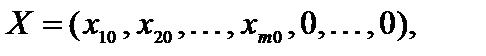 для которого векторы условий, соответствующие положительным координатам
для которого векторы условий, соответствующие положительным координатам 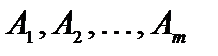 , являются линейно независимыми.
, являются линейно независимыми.
Число отличных от нуля координат опорного решения не может быть больше ранга r-системы векторов условий (числа линейно независимых уравнений системы ограничений). В дальнейшем будем считать, что система ограничений состоит из линейно независимых уравнений, т. е. m = r.
Есличисло отличных от нуля координат опорного решения равно m, то оно называется невырожденным, в противном случае (меньше m) вырожденным.
Базисом опорного решения называется базис системы векторов условий задачи, включающий в свой состав векторы, соответствующие отличным от нуля координатам опорного решения.
Докажем две теоремы о взаимосвязи опорных решений и угловых точек области допустимых решений.
Теорема 4.4. Любое опорное решение является угловой точкой области допустимых решений.
Доказательство. Пусть 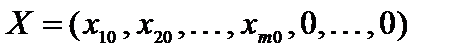 – опорное решение с базисом
– опорное решение с базисом 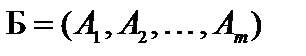 некоторой задачи с системой ограничений
некоторой задачи с системой ограничений 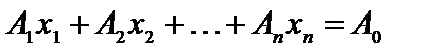 . Предположим, что X – не угловая точка, тогда оно является выпуклой линейной комбинацией каких- либо точек области допустимых решений, например,
. Предположим, что X – не угловая точка, тогда оно является выпуклой линейной комбинацией каких- либо точек области допустимых решений, например, 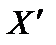 и
и 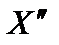 , т. е.
, т. е.
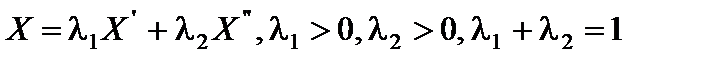 .
.
Так как последние n - m координат вектора X равны нулю, а 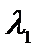 и
и 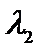 положительные, то последние n - m координат векторов
положительные, то последние n - m координат векторов 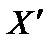 и
и 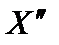 также равны нулю, т. е.
также равны нулю, т. е. 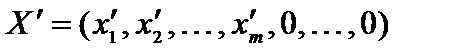 и
и 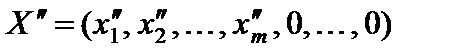 .
.
Подставим 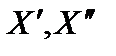 в систему ограничений.
в систему ограничений.
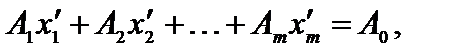
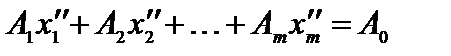 .
.
Вычтем из первого равенства второе, получим
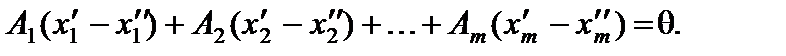
Так как векторы 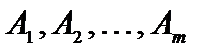 образуют базис, то они линейно независимые, а потому данное равенство может выполняться только тогда, когда все коэффициенты при векторах равны нулю, т. е.
образуют базис, то они линейно независимые, а потому данное равенство может выполняться только тогда, когда все коэффициенты при векторах равны нулю, т. е.
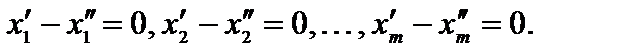
Отсюда получаем 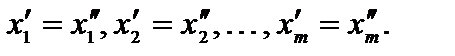 Следовательно,
Следовательно, 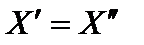 и опорное решение X не является выпуклой линейной комбинацией каких-либо допустимых решений, а является угловой точкой области допустимых решений.
и опорное решение X не является выпуклой линейной комбинацией каких-либо допустимых решений, а является угловой точкой области допустимых решений.
Теорема 4.5. Любая угловая точка области допустимых решений является опорным решением.
Доказательство. Пусть 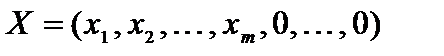 угловая точка области допустимых решений и
угловая точка области допустимых решений и 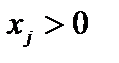 при j = 1, 2,…, m. Чтобы доказать, что это решение является опорным, достаточно показать, что векторы
при j = 1, 2,…, m. Чтобы доказать, что это решение является опорным, достаточно показать, что векторы 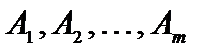 , соответствующие положительным координатам решения, являются линейно независимыми. Предположим, что эти векторы линейно зависимые. Тогда существует ненулевой набор чисел
, соответствующие положительным координатам решения, являются линейно независимыми. Предположим, что эти векторы линейно зависимые. Тогда существует ненулевой набор чисел 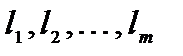 такой, что
такой, что

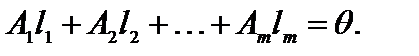 (3.2)
(3.2)
Так как X допустимое решение, то имеет место равенство
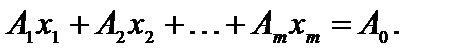 (3.3)
(3.3)
Умножим соотношение (3.2) на некоторое число 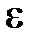 и прибавим к равенству (3.3), получим
и прибавим к равенству (3.3), получим
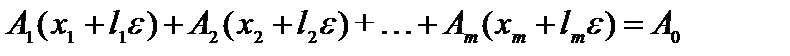 ,
,
т. е. вектор 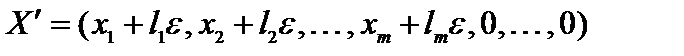 является решением системы ограничений задачи. Аналогично можно показать, что решением системы будет также вектор
является решением системы ограничений задачи. Аналогично можно показать, что решением системы будет также вектор
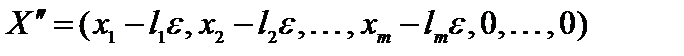 .
.
Для того чтобы эти векторы 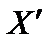 и
и 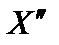 удовлетворяли условиям неотрицательности, достаточно малое число e выбирать таким, что
удовлетворяли условиям неотрицательности, достаточно малое число e выбирать таким, что 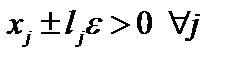 . Это возможно, так как
. Это возможно, так как 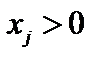 при j = 1, 2,…, m.. При таком выборе числа
при j = 1, 2,…, m.. При таком выборе числа 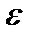 векторы
векторы 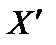 и
и 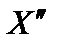 считаются допустимыми. Нетрудно увидеть, что
считаются допустимыми. Нетрудно увидеть, что 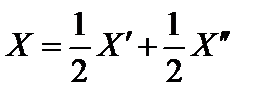 , т. е. X – выпуклая линейная комбинация
, т. е. X – выпуклая линейная комбинация 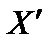 и
и 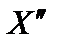 . Однако это противоречит тому, что X является угловой точкой. Следовательно, векторы
. Однако это противоречит тому, что X является угловой точкой. Следовательно, векторы 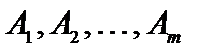 линейно независимые, и решение X является опорным.
линейно независимые, и решение X является опорным.
Лекция№5-6.
СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ
ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Это метод целенаправленного перебора опорных решений задачи линейного программирования, поэтому его часто называют методом улучшения опорных решений.
Симплексный метод позволяет выполнить следующее:
1) найти начальное опорное решение;
2) перейти к новому опорному решению, на котором значение целевой функции будет ближе к оптимальному решению, т. е. улучшить опорное решение;
3) своевременно прекратить перебор опорных решений, остановившись на оптимальном решении, или сделать заключение об отсутствии оптимального решения.
Название метод получил от вида области допустимых решений задачи, для которой он первоначально применялся. Область допустимых решений этой задачи имела простейший (simple) вид (рис. 3.6).
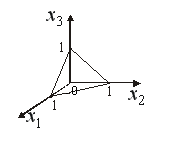
Рис. 3.6
Дата добавления: 2017-05-18; просмотров: 1640;
