Лекция №3 ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Графический метод решения задач линейного программирования с n переменными

Данным методом решаются задачи линейного программирования, имеющие каноническую форму и удовлетворяющие условию 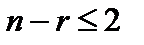, где n – число неизвестных системы, r – ранг системы векторов-условий (число линейно независимых уравнений системы). Если уравнения системы ограничений линейно независимые, то r = m.

Рассмотрим алгоритм метода на конкретном примере.

Пример 2.6. Решить графическим методом.

,

.

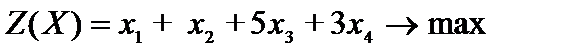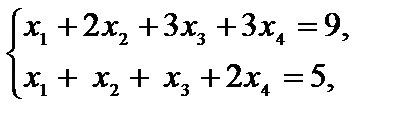
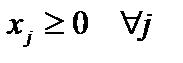Решение.

1. Проверяем условие применимости графического метода. Нетрудно видеть, что любые два из векторов-столбцов системы ограничений, например, 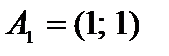, 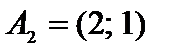являются линейно независимыми, так как их координаты непропорциональны, поэтому ранг системы векторов-условий r = 2. Находим n - r = 4 - 2 =2 £ 2. Следовательно, метод применим.

2. Приведем систему ограничений-уравнений к равносильной, разрешенной с помощью метода Жордана – Гаусса. Одновременно исключим разрешенные неизвестные из целевой функции. Для этого

Т а б л и ц а 2.1

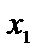
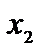
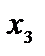
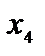
				b
				–5
		–1
				–5

запишем коэффициенты целевой функции в последней (третьей) строке таблицы, под матрицей системы. Вычисления приведены в табл. 2.1. Задача после проведенных преобразований

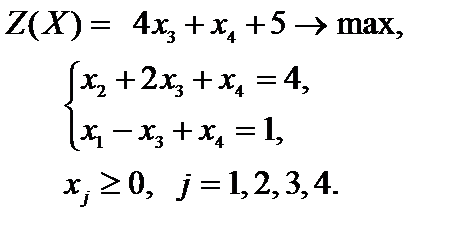
3. Отбросим в уравнениях-ограничениях неотрицательные разрешенные неизвестные 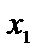и и 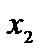заменим знаки равенства знаками " 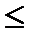", получим эквивалентную задачу линейного программирования с двумя переменными

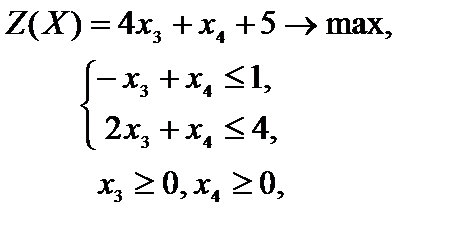
которая решается графическим методом (рис. 2.8).

Рис. 2.8

Оптимальное решение 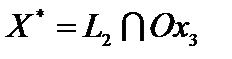; = (2; 0). Значение целевой функции 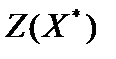= 4 × 2 + 0 + 5 = 13.

4. Используем систему ограничений исходной задачи, приведенную к каноническому виду,

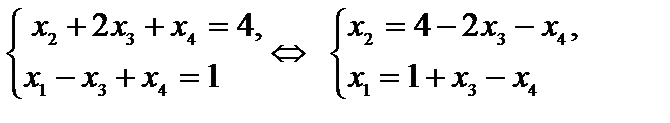
и оптимальное решение задачи с двумя переменными = (2; 0) для нахождения оптимального решения исходной задачи

;

.

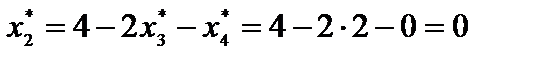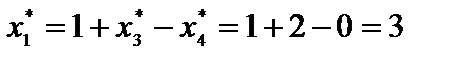Записываем оптимальное решение исходной задачи
= (3; 0; 2; 0). Значение целевой функции на оптимальном решении совпадает со значением целевой функции для вспомогательной задачи 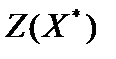= 1 × 3 + 2 × 0 + 5 × 2 + 3 × 0 = 13.

Ответ: max Z(X) = 13 при = (3; 0; 2; 0).