Каноническая форма задачи линейного программирования

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В том случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Она может быть представлена в координатной, векторной или матричной записи.

1. Каноническая задача линейного программирования в координатной записи имеет вид

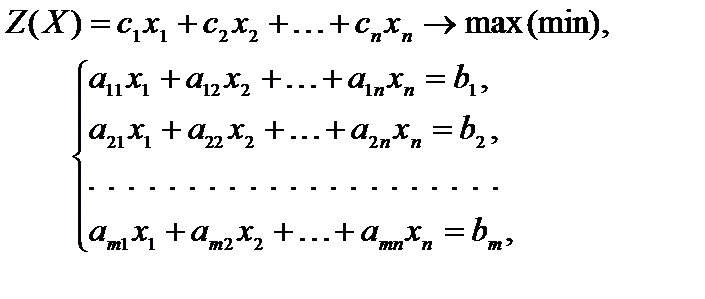(1.6)

.

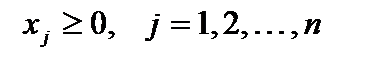В более компактной форме данную задачу можно записать, используя знак суммирования,

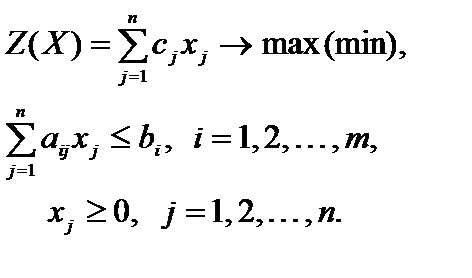(1.7)

2. Каноническая задача линейного программирования в векторной записи имеет вид

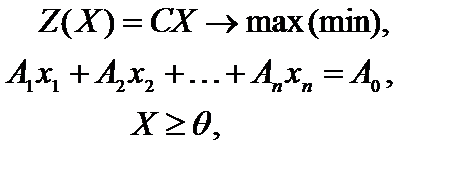(1.8)

где ,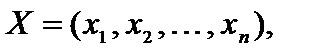

.

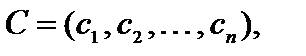
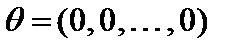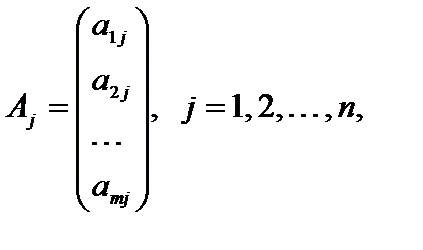
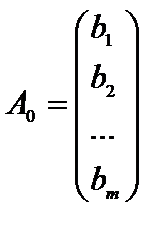3. Каноническая задача линейного программирования в матричной записи имеет вид

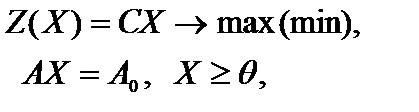(1.9)

где

, .

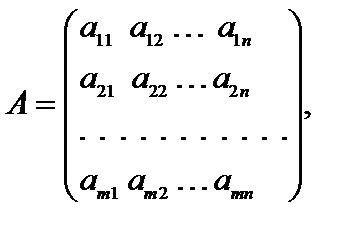
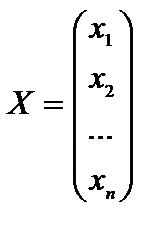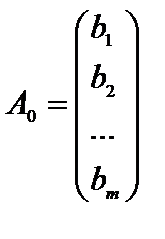Здесь А – матрица коэффициентов системы уравнений, Х – матрица-столбец переменных задачи, 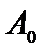– матрица-столбец правых частей системы ограничений.

Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной записи имеют вид

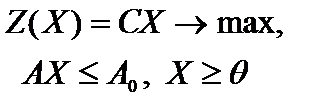(1.10)

или

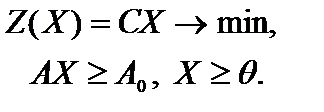(1.11)