Примеры составления математических моделей задач линейного программирования
Задача использования ресурсов (сырья). Для изготовления n видов продукции используется m видов ресурсов (сырья). Известны: 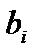 (i =1, 2, ..., m) – запасы каждого i-го вида ресурса (сырья);
(i =1, 2, ..., m) – запасы каждого i-го вида ресурса (сырья);
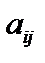 , (i =1, 2, ..., m; j = 1, 2, 3, ..., n)– затраты каждого i-го вида ресурса (сырья) на производство единицы объема j-го вида продукции;
, (i =1, 2, ..., m; j = 1, 2, 3, ..., n)– затраты каждого i-го вида ресурса (сырья) на производство единицы объема j-го вида продукции;
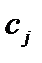 (j = 1, 2, 3, ..., n) –прибыль от реализации единицы объема j-го вида продукции. Требуется составить план производства продукции, который обеспечивает максимум прибыли при заданных ограничениях на ресурсы (сырье).
(j = 1, 2, 3, ..., n) –прибыль от реализации единицы объема j-го вида продукции. Требуется составить план производства продукции, который обеспечивает максимум прибыли при заданных ограничениях на ресурсы (сырье).
Решение. Введем вектор переменных задачи 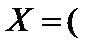
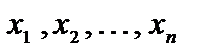 ), где
), где 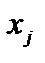 (j = 1, 2, ..., n) – объем производства j-го вида продукции. Затраты i-го вида ресурса (сырья) на изготовление данного объема
(j = 1, 2, ..., n) – объем производства j-го вида продукции. Затраты i-го вида ресурса (сырья) на изготовление данного объема 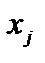 продукции равны
продукции равны 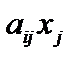 , поэтому ограничение на использование этого вида ресурса (сырья) имеет вид
, поэтому ограничение на использование этого вида ресурса (сырья) имеет вид 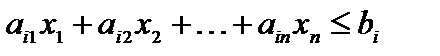 . Прибыль от реализации j-го вида продукции равна
. Прибыль от реализации j-го вида продукции равна 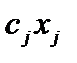 , поэтому целевая функция
, поэтому целевая функция 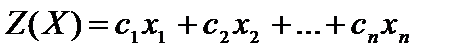 .
.
Математическая модель имеет вид
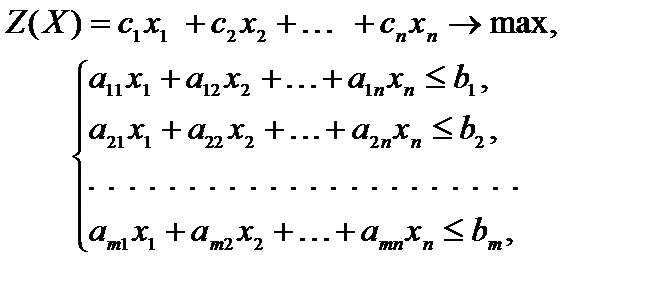
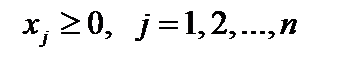 .
.
Задача составления рациона. Для полноценного откорма каждое животное должно получать ежедневно m питательных веществ в количествах не менее 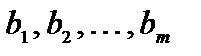 . В рацион животных входят n видов кормов. Известно:
. В рацион животных входят n видов кормов. Известно: 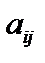 (i =1, 2, ..., m; j = 1, 2, 3, ..., n) – содержание i-го питательного вещества в единице j-го вида корма;
(i =1, 2, ..., m; j = 1, 2, 3, ..., n) – содержание i-го питательного вещества в единице j-го вида корма;
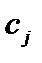 (j = 1, 2, 3, ..., n) – стоимость единицы j-го вида корма. Требуется составить суточный рацион полноценного откорма животных, обеспечивающий минимальные затраты.
(j = 1, 2, 3, ..., n) – стоимость единицы j-го вида корма. Требуется составить суточный рацион полноценного откорма животных, обеспечивающий минимальные затраты.
Решение. Введем переменные задачи 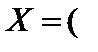
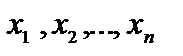 ), где
), где
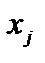 (j = 1, 2,..., n)– объем j-го вида корма, входящего в суточный рацион. Так как
(j = 1, 2,..., n)– объем j-го вида корма, входящего в суточный рацион. Так как 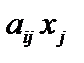 – количество i-го питательного вещества, содержащегося в j-м виде корма,
– количество i-го питательного вещества, содержащегося в j-м виде корма, 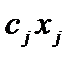 – стоимость j-го вида корма, входящего в суточный рацион, то математическая модель имеет вид
– стоимость j-го вида корма, входящего в суточный рацион, то математическая модель имеет вид
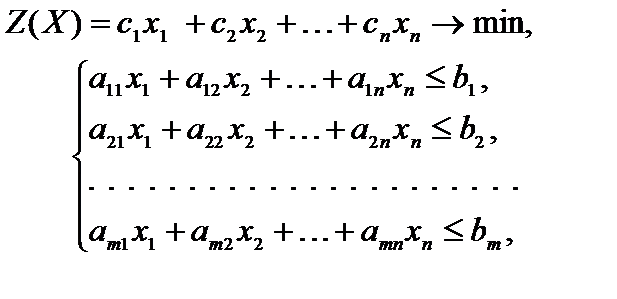
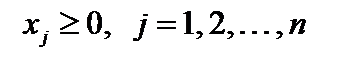 .
.
Дата добавления: 2017-05-18; просмотров: 788;
