Приведение общей задачи линейного программирования к канонической форме
В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако при составлении математических моделей экономических задач ограничения в основном формируются в системы неравенств, поэтому необходимо уметь переходить от системы неравенств к системе уравнений. С этой целью докажем следующую теорему.
Теорема 1.1. О замене неравенства уравнением. Каждому решению 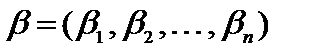 неравенства
неравенства
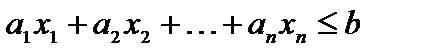 (1.12)
(1.12)
соответствует единственное решение 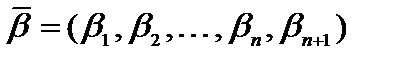 уравнения
уравнения
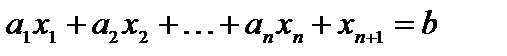 (1.13)
(1.13)
и неравенства
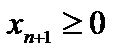 , (1.14)
, (1.14)
и, наоборот, каждому решению 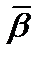 уравнения (1.13) и неравенства (1.14) соответствует единственное решение
уравнения (1.13) и неравенства (1.14) соответствует единственное решение 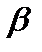 неравенства (1.12).
неравенства (1.12).
Доказательство. Пусть 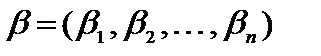 – решение неравенства (1.12), тогда
– решение неравенства (1.12), тогда 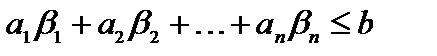 . Обозначим разность правой и левой частей этого неравенства через
. Обозначим разность правой и левой частей этого неравенства через 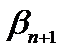 , т. е.
, т. е.
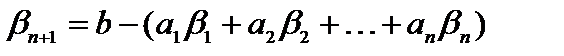 .
.
Очевидно 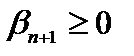 . Подставим в уравнение (1.13) вместо переменных значения
. Подставим в уравнение (1.13) вместо переменных значения 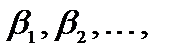
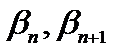 , получим
, получим 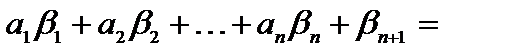
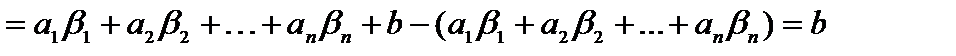 .
.
Таким образом, 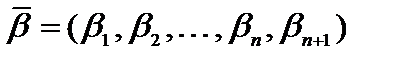 удовлетворяет уравнению (1.13) и неравенству (1.14). Значит доказана первая часть теоремы.
удовлетворяет уравнению (1.13) и неравенству (1.14). Значит доказана первая часть теоремы.
Пусть теперь 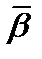 удовлетворяет уравнению (1.13) и неравенству (1.14), т. е. имеем
удовлетворяет уравнению (1.13) и неравенству (1.14), т. е. имеем
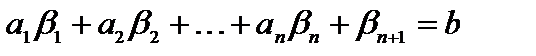 и
и 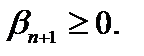
Отбрасывая в левой части последнего равенства неотрицательную величину 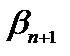 , получаем
, получаем
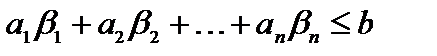 ,
,
т. е. 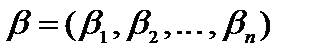 удовлетворяет неравенству (1.12). Теорема доказана.
удовлетворяет неравенству (1.12). Теорема доказана.
Если неравенство 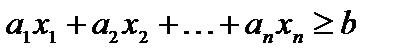 , то дополнительную неотрицательную переменную
, то дополнительную неотрицательную переменную 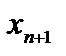 необходимо ввести в его левую часть со знаком минус, т. е.
необходимо ввести в его левую часть со знаком минус, т. е. 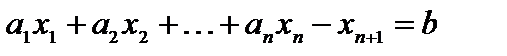 .
.
Неотрицательные переменные, вводимая в ограничения неравенства для превращения их в уравнения, называются дополнительными переменными. Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значение.
В том случае, когда задача имеет произвольно изменяющиеся переменные, то любую такую переменную 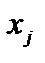 заменяют разностью двух неотрицательных переменных, т. е.
заменяют разностью двух неотрицательных переменных, т. е. 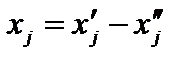 , где
, где 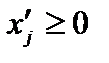 и
и 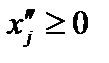 .
.
Иногда возникает необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций на оптимальных решениях отличаются только знаком.
Пример 1.1. Привести к каноническому виду задачу линейного программирования.
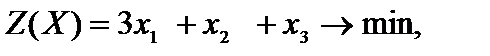
| Д |
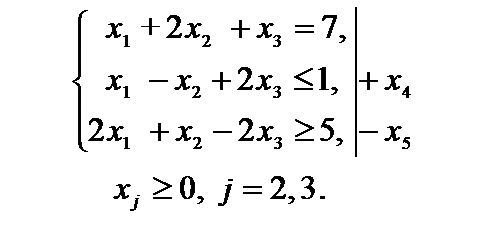
Решение. Перейдем к задаче на отыскание максимума целевой функции. Для этого изменим знаки коэффициентов целевой функции. Для превращения в уравнения второго и третьего неравенств системы ограничений введем неотрицательные дополнительные переменные 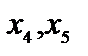 (на математической модели эта операция отмечена буквой Д). Переменная
(на математической модели эта операция отмечена буквой Д). Переменная 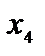 вводится в левую часть второго неравенства со знаком "+", так как неравенство имеет вид
вводится в левую часть второго неравенства со знаком "+", так как неравенство имеет вид 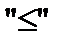 . Переменная
. Переменная 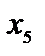 вводится в левую часть третьего неравенства со знаком "-", так как неравенство имеет вид
вводится в левую часть третьего неравенства со знаком "-", так как неравенство имеет вид 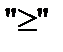 . В целевую функцию переменные
. В целевую функцию переменные 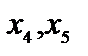 вводятся с коэффициентом, равным нулю. Переменную
вводятся с коэффициентом, равным нулю. Переменную 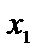 , на которую не наложено условие неотрицательности заменяем разностью
, на которую не наложено условие неотрицательности заменяем разностью 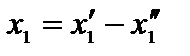 ,
, 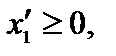
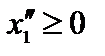 . Записываем задачу в каноническом виде
. Записываем задачу в каноническом виде
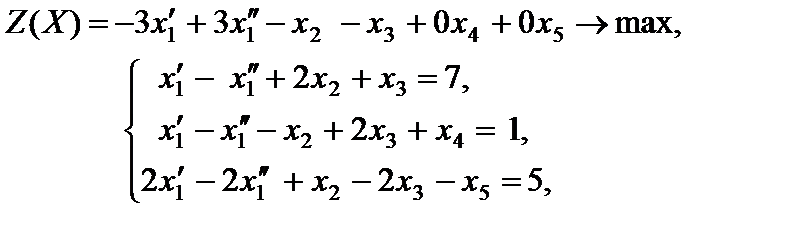
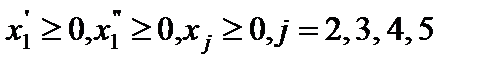 .
.
В некоторых случаях возникает необходимость приведения канонической задачи к симметричной задаче. Рассмотрим пример.
Пример 1.2. Привести к симметричному виду задачу линейного программирования
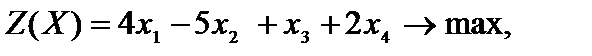
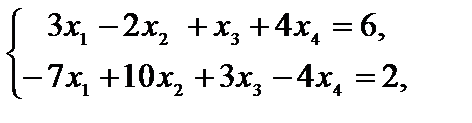
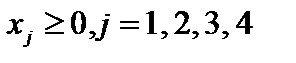 .
.
Решение. Методом Жордана-Гаусса приведем систему уравнений-ограничений задачи к равносильной разрешенной. Одновременно разрешенные неизвестные исключим из целевой функции. Для этого в таблице решения задачи (табл. 1.1) наряду с коэффициентами уравнений системы ограничений в дополнительной строке запишем коэффициенты целевой функции. В последнем столбце дополнительной строки (на месте правой части уравнений) запишем свободный член целевой функции, равный нулю. При вычислениях учитываем, что разрешающий элемент в последней строке (в целевой функции) выбирать нельзя.
Т а б л и ц а 1.1
| x1 | x2 | x3 | x4 | b | ||
| –2 | x(–3) | x(–1) | ||||
| –7 | –4 | + | ||||
| –5 | Целевая функция | |||||
| –2 | 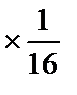
| |||||
| –16 | –16 | –16 | ||||
| –3 | –2 | –6 | ||||
| –2 | + | |||||
| –1 | –1 | –1 | ´2 ´3 | |||
| –3 | –2 | –6 | + | |||
| –1 | –1 | –1 | ||||
| –2 | –5 | –9 |
Число -9, полученное в последнем столбце последней строки таблицы необходимо записать в целевую функцию с противоположным знаком. В результате данных преобразований задача принимает следующий вид:
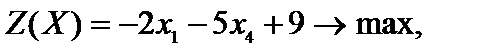
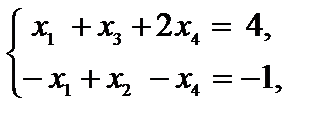
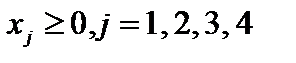 .
.
Так как переменные 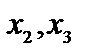 неотрицательные, отбросив их, можно записать задачу в симметричном виде
неотрицательные, отбросив их, можно записать задачу в симметричном виде
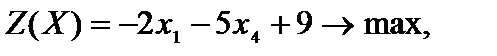
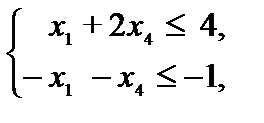
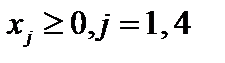 .
.
Дата добавления: 2017-05-18; просмотров: 3184;
