Теорема об экстремуме целевой функции

Теорема 3.3. Об экстремуме целевой функции. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, то она также достигает экстремума в любой выпуклой линейной комбинации этих точек.

Доказательство. Будем считать, что решается задача на нахождение максимума целевой функции

Z(X) = CX 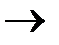max,

AX = ,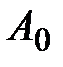

.

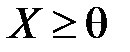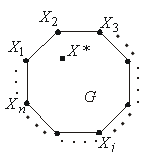
Рис. 3.5

1. Докажем, что целевая функция достигает экстремума в угловой точке области допустимых решений G, от противного. Если – оптимальное решение, то 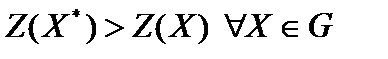. Предположим, что оптимальное решение задачи не является угловой точкой (рис.3.5). Тогда по теореме 3.1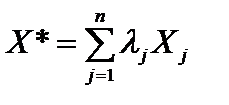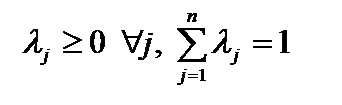

,

где , где 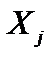(j = 1, 2, …, n) – угловые точки G.

Найдем

.

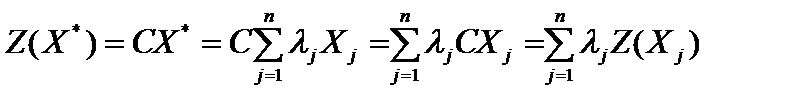Среди значений 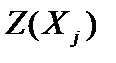выберем наибольшее. Пусть это будет 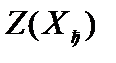, т. е. 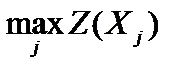= 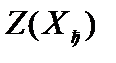. Тогда

.

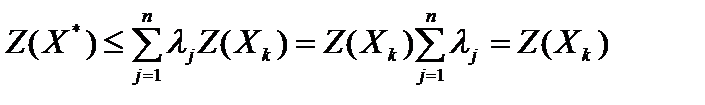Это противоречит тому, что является оптимальным решением (в задаче на максимум 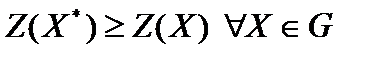). Следовательно, – угловая точка G области допустимых решений.

2. Докажем второе утверждение теоремы. Пусть угловые точки области допустимых решений являются оптимальными решениями, т. е. 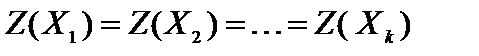и . Найдем значение целевой функции для некоторой выпуклой линейной комбинации этих угловых точек

,

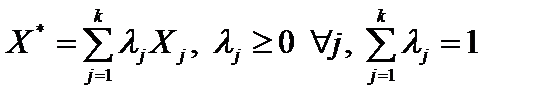получим

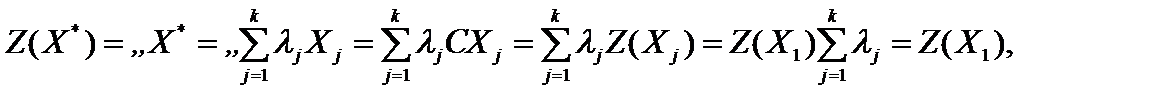т. е. решение также является оптимальным.