Преобразование целевой функции при переходе от одного опорного решения к другому
Пусть имеется опорное решение задачи линейного программирования (4.1)-(4.3) 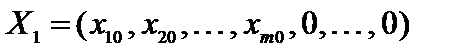 c базисом
c базисом 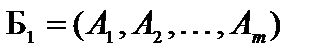 . Значение целевой функции задачи на этом этапе решения равно
. Значение целевой функции задачи на этом этапе решения равно 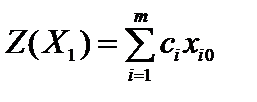 . Используя преобразование Жордана с разрешающим элементом
. Используя преобразование Жордана с разрешающим элементом 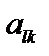 , перейдем к другому опорному решению
, перейдем к другому опорному решению 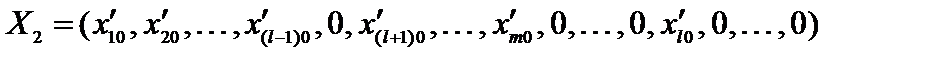 с базисом
с базисом 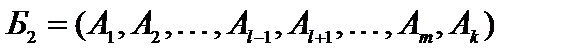 , т. е. введем в базис вектор
, т. е. введем в базис вектор 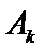 и исключим
и исключим 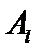 . Значение целевой функции на этом этапе решения равно
. Значение целевой функции на этом этапе решения равно
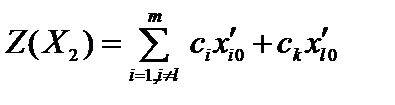 .
.
Формулы пересчета правых частей уравнений системы при преобразовании Жордана имеют вид
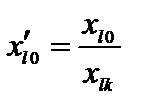 ;
; 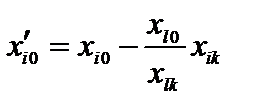 ; i = 1, 2, …, m; i ¹ l.
; i = 1, 2, …, m; i ¹ l.
Используя эти формулы, получим
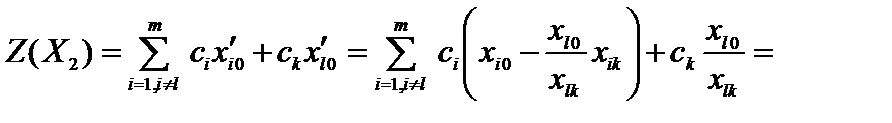
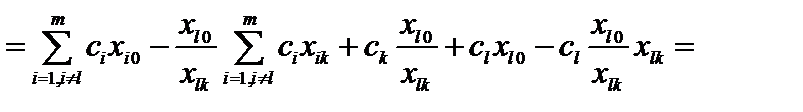
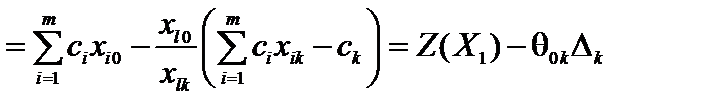 ,
,
т. е. 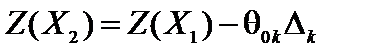 . (4.6)
. (4.6)
Отсюда находим приращение целевой функции при переходе от одного опорного решения к другому
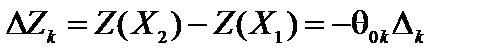 . (4.7)
. (4.7)
Здесь через 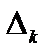 обозначена величина, называемая оценкой разложения вектора условий
обозначена величина, называемая оценкой разложения вектора условий 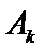 по базису опорного решения и вычисляемая по формуле
по базису опорного решения и вычисляемая по формуле
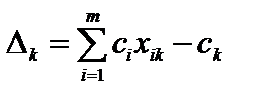 (4.8)
(4.8)
или в векторной записи
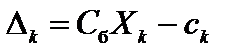 , (4.9)
, (4.9)
где 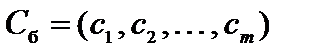 - вектор коэффициентов целевой функции при базисных переменных,
- вектор коэффициентов целевой функции при базисных переменных, 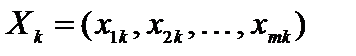 - вектор коэффициентов разложения вектора
- вектор коэффициентов разложения вектора 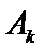 по базису опорного решения,
по базису опорного решения, 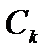 - коэффициент целевой функции при переменной
- коэффициент целевой функции при переменной 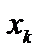 .
.
Пример 4.2. Вычислить оценки 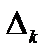 разложений векторов условий по базису опорного решения для следующей задачи:
разложений векторов условий по базису опорного решения для следующей задачи:
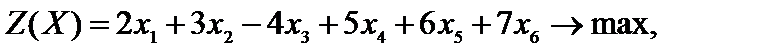
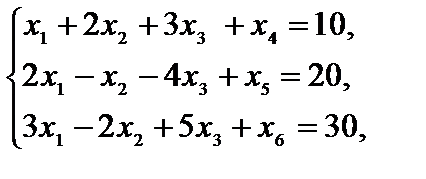
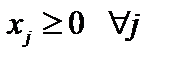 .
.
Решение. Задача имеет начальное опорное решение 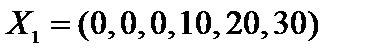 с базисом
с базисом 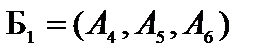 . Для удобства расчета запишем исходные данные в следующую таблицу, называемую симплексной (табл. 4.2).
. Для удобства расчета запишем исходные данные в следующую таблицу, называемую симплексной (табл. 4.2).
Т а б л и ц а 4.2
| -4 | |||||||
| Б Сб | 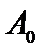
| 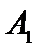
| 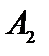
| 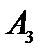
| 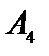
| 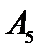
| 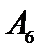
|
| -1 | -4 | ||||||
| -2 | |||||||
| -13 |
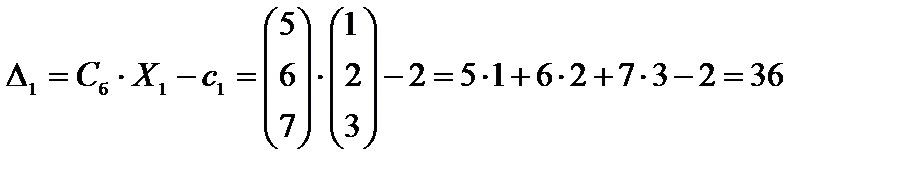 ;
;
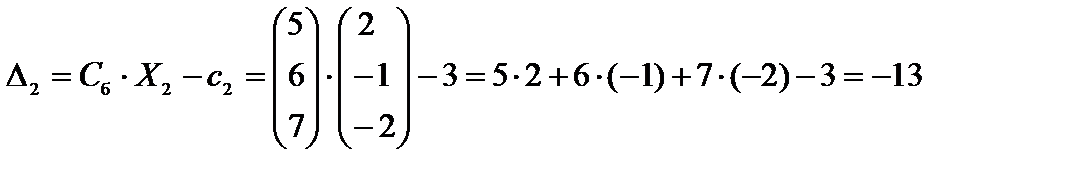 ;
;
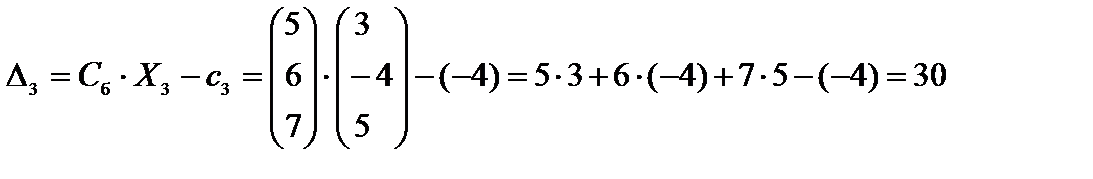 .
.
Оценки для векторов, входящих в базис, всегда равны нулю.
Дата добавления: 2017-05-18; просмотров: 1146;
