Общие правила составления двойственных задач
1. Одна из пары двойственных задач на максимума, а другая на минимум. При этом в задаче на максимум все ограничения неравенства типа "£", а в задаче на минимум – "³".
2. Каждому ограничению исходной задачи соответствует переменная (оценка) двойственной задачи. При этом ограничению неравенства соответствует переменная, удовлетворяющая условию неотрицательности, а ограничению уравнения – переменная, на которую не налагается условие неотрицательности.
3. Матрицей системы ограничений двойственной задачи выступает транспонированная матрица системы ограничений исходной задачи.
4. Коэффициентами целевой функции двойственной задачи являются правые части системы ограничений исходной задачи, а правыми частями системы ограничений двойственной задачи будут коэффициенты целевой функции исходной задачи.
Пример 5.1. Составить задачу, двойственную к данной
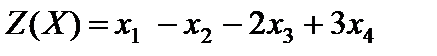 ® min,
® min,
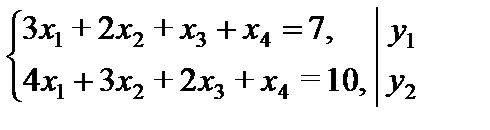
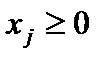 , j = 1, 2, 3, 4.
, j = 1, 2, 3, 4.
Решение. Данная задача имеет вид исходной задачи второй несимметричной пары двойственных задач (5.10). Записываем двойственную задачу
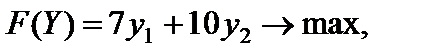
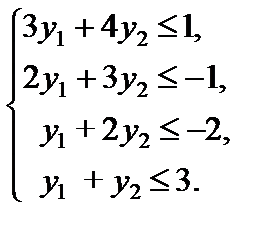
Переменные 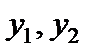 не удовлетворяют условию неотрицательности, так как они соответствуют ограничениям равенства исходной задачи.
не удовлетворяют условию неотрицательности, так как они соответствуют ограничениям равенства исходной задачи.
Пример 5.2. Составить задачу, двойственную к данной
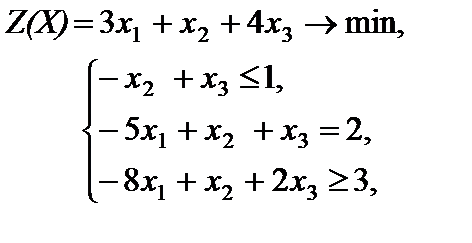
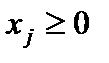 , j = 1, 2, 3.
, j = 1, 2, 3.
Решение. Так как в исходной задаче требуется найти минимум целевой функции, то все ограничения должны быть типа " ³ " (правило 1). Поэтому умножим первое неравенство в системе ограничений на -1. Задача примет вид
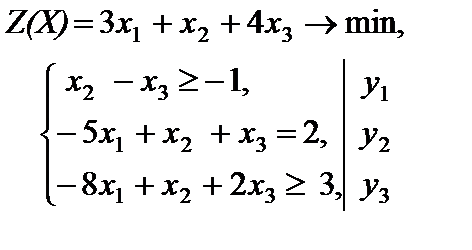
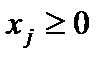 , j = 1, 2, 3.
, j = 1, 2, 3.
Трем ограничениям исходной задачи соответствуют три переменных 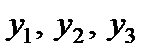 двойственной задачи. При этом переменные
двойственной задачи. При этом переменные 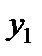 и
и 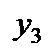 должны удовлетворять условию неотрицательности, так как первое и третье ограничения исходной задачи – это неравенства, а на
должны удовлетворять условию неотрицательности, так как первое и третье ограничения исходной задачи – это неравенства, а на 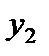 не налагается условие неотрицательности, поскольку второе ограничение является уравнением (правило 2).
не налагается условие неотрицательности, поскольку второе ограничение является уравнением (правило 2).
Так как правые части системы ограничений исходной задачи являются коэффициентами целевой функции F(Y) двойственной задачи (правило 4), то 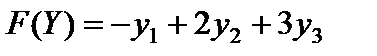 . Причем необходимо находить максимум этой функции, так как исходная задача на минимум (правило 1).
. Причем необходимо находить максимум этой функции, так как исходная задача на минимум (правило 1).
Матрицей системы ограничений двойственной задачи является транспонированная матрица исходной задачи (правило 3). Ее правыми частями являются коэффициенты целевой функции исходной задачи (правило 4). Все ограничения в задаче на максимум имеют тип "£" (правило 1) и являются неравенствами, так как все переменные исходной задачи удовлетворяют условию неотрицательности (правило 2). Двойственная задача имеет вид
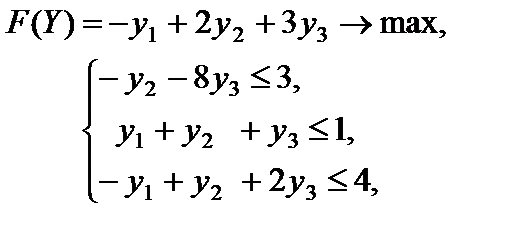
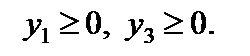
Дата добавления: 2017-05-18; просмотров: 1067;
