Различные виды уравнения прямой на плоскости.
1. Любая линейная связь между переменными 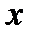 и
и 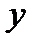 вида
вида
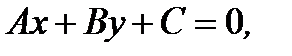 (2.34)
(2.34)
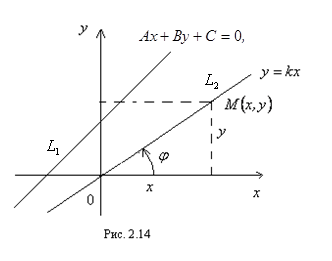
где действительные числа 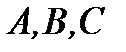 одновременно не равны нулю, описывает прямую на плоскости. (2.34) есть общий вид уравнения прямой на плоскости (рис. 2.14, прямая
одновременно не равны нулю, описывает прямую на плоскости. (2.34) есть общий вид уравнения прямой на плоскости (рис. 2.14, прямая 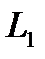 ).
).
2. Из (2.34), считая 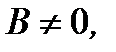 найдем
найдем
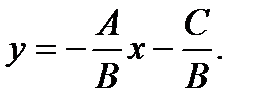 (2.35)
(2.35)
Обозначая
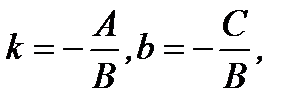 (2.36)
(2.36)
из (2.35) получим уравнение прямой с угловым коэффициентом 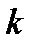
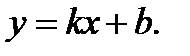 (2.37)
(2.37)
В частном случае, когда 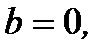 уравнение (2.37) принимает вид
уравнение (2.37) принимает вид
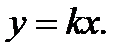 (2.38)
(2.38)
Отсюда имеем
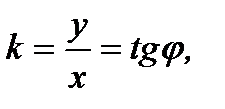 (2.39)
(2.39)
где 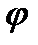 есть угол между прямой и положительным направлением оси
есть угол между прямой и положительным направлением оси 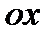 (рис. 2.14, прямая
(рис. 2.14, прямая 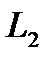 ).
).
3. Преобразуя общий вид уравнения прямой (2.34) к виду 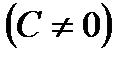
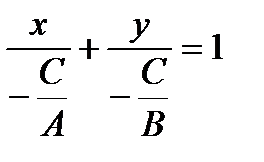 (2.40)
(2.40)

и обозначая 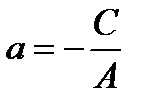 и
и 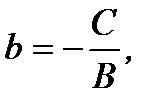 получим
получим
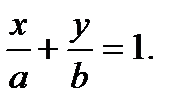 (2.41)
(2.41)
(2.41) есть уравнение прямой на плоскости в отрезках. Числа 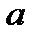 и
и 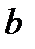 показывают отрезки, отсекающие прямой на осях
показывают отрезки, отсекающие прямой на осях 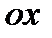 и
и  . Действительно, если
. Действительно, если 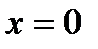 , то из (2.41) следует, что
, то из (2.41) следует, что 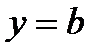 и если
и если 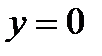 , то из (2.41) следует, что
, то из (2.41) следует, что 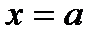 (рис. 2.15, прямая
(рис. 2.15, прямая 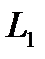 ).
).
4. Уравнение прямой, проходящей через две заданные точки 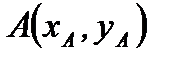 и
и 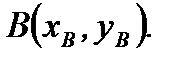
Пусть уравнение искомой прямой имеет вид
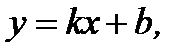 (2.42)
(2.42)
где  и
и 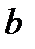 пока неизвестные величины. Для определения этих неизвестных воспользуемся тем, что точки
пока неизвестные величины. Для определения этих неизвестных воспользуемся тем, что точки 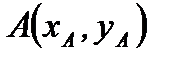 и
и 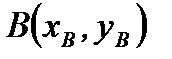 лежат на прямой, то есть координаты этих точек удовлетворяют уравнению прямой (2.42) (рис. 2.15, прямая
лежат на прямой, то есть координаты этих точек удовлетворяют уравнению прямой (2.42) (рис. 2.15, прямая 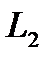 ).
).
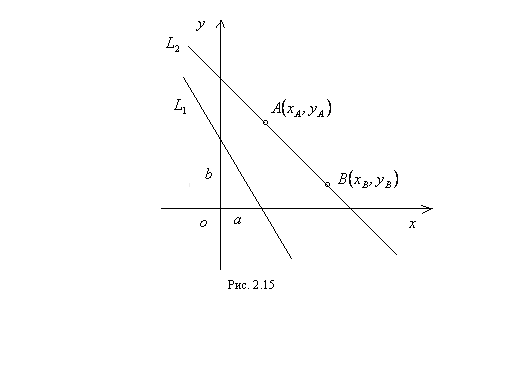
Имеем
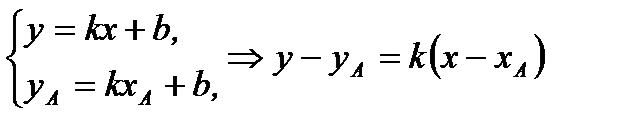 ,
, 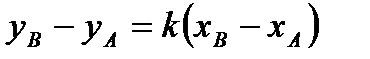 ,
, 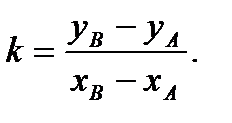 (2.43)
(2.43)
Подставляя найденное значение 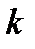 во второе уравнение системы (2.43) и производя некоторые преобразования, получим уравнение прямой, проходящей через две заданные точки, в виде
во второе уравнение системы (2.43) и производя некоторые преобразования, получим уравнение прямой, проходящей через две заданные точки, в виде
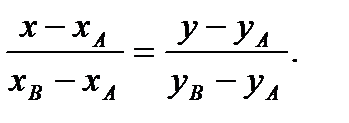 (2.44)
(2.44)
5. Нормированное уравнение прямой. Расстояние точки от прямой.
При решении задачи нахождения расстояния заданной точки от заданной прямой мы должны пользоваться уравнением прямой в нормированном виде.
Пусть дана прямая 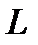 . Нормаль этой прямой обозначим через
. Нормаль этой прямой обозначим через 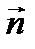 , а единичный вектор этой нормали обозначим через
, а единичный вектор этой нормали обозначим через 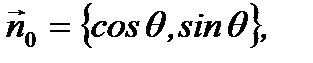 где
где 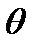 есть угол между нормальным вектором
есть угол между нормальным вектором 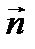 и осью
и осью 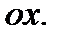 Возьмем на прямой точку
Возьмем на прямой точку 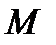 с текущими координатами
с текущими координатами 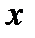 и
и 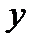
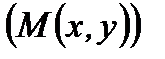 , а вне прямой возьмем точку
, а вне прямой возьмем точку 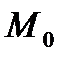 с заданными координатами
с заданными координатами 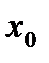 и
и 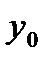
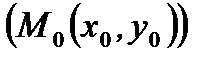 (рис. 2.16). Очевидно, что
(рис. 2.16). Очевидно, что 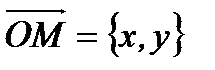 и
и 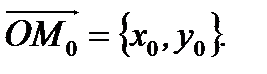 Точку пересечения нормали с прямой обозначим через
Точку пересечения нормали с прямой обозначим через 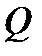 , длину отрезка
, длину отрезка 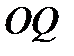 обозначим через
обозначим через 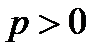 и заметим, что
и заметим, что 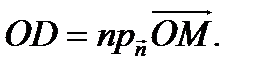 Рассмотрим скалярное произведение векторов
Рассмотрим скалярное произведение векторов 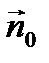 и
и 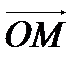 . Имеем с одной стороны
. Имеем с одной стороны 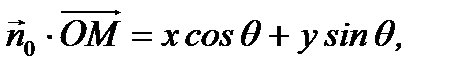 a с другой стороны
a с другой стороны 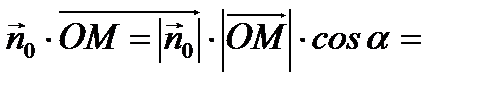
 То есть
То есть
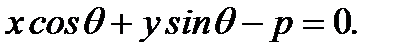 (2.45)
(2.45)
(2.45) представляет нормированное уравнение прямой на плоскости. Из рисунка 2.16 видно, что 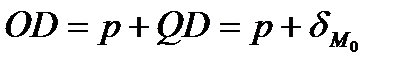 или
или 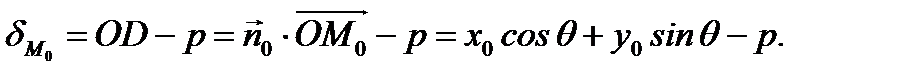
Величина 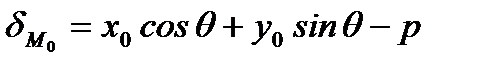 называется отклонением точки
называется отклонением точки 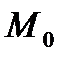 от прямой
от прямой 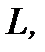 причем
причем 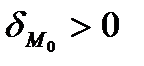 , если точка
, если точка 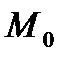 и начало координат находятся по разные стороны прямой
и начало координат находятся по разные стороны прямой 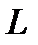 и
и 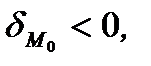 если точка
если точка 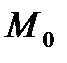 и начало координат находятся по одну сторону прямой
и начало координат находятся по одну сторону прямой 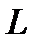 (если
(если 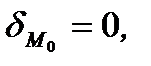 то точка
то точка 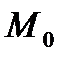 принадлежит прямой
принадлежит прямой 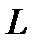 ). Расстояние точки
). Расстояние точки 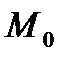 от прямой
от прямой 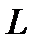
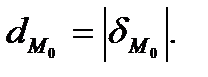
Как привести общее уравнение прямой (2.34) на плоскости к нормированному виду (2.45)? Для этого нужно обе части уравнения (2.34) умножить на нормирующий множитель 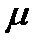 , то есть
, то есть

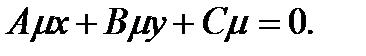 (2.46)
(2.46)
Сравнивая (2.46) с (2.45), получим
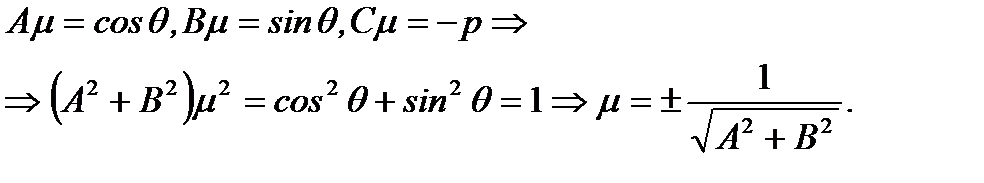 (2.47)
(2.47)
При этом, как видно из (2.47), если 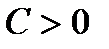 , то
, то 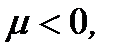 а если
а если  то
то 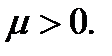
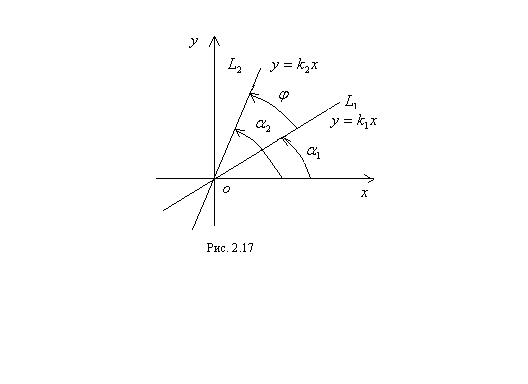
Пример 2.11.Найти угол между прямыми 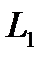 и
и 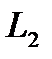 , уравнения которых имеют вид:
, уравнения которых имеют вид: 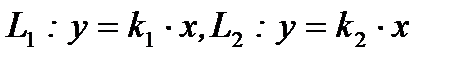 (рис. 2.17).
(рис. 2.17).
Решение.Из рисунка (2.17) следует, что
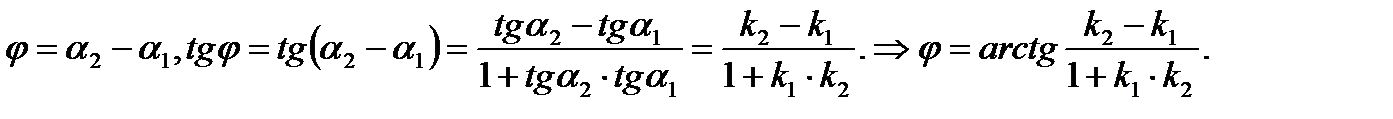 (2.48)
(2.48)
Ответ: 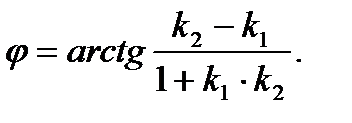
Из (2.48) следует, что если прямые перпендикулярны 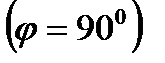 , то удовлетворяется условие
, то удовлетворяется условие 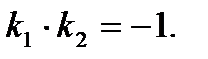
Пример 2.12.Даны координаты вершины 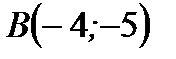 треугольника
треугольника 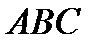 и уравнения двух высот:
и уравнения двух высот:  Найти уравнения сторон треугольника
Найти уравнения сторон треугольника 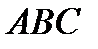 (рис. 2.18).
(рис. 2.18).

Решение.Решая уравнения высот 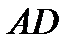 и
и 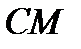 относительно
относительно 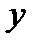 , получим
, получим
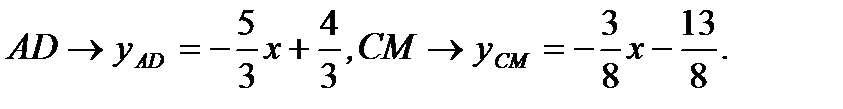 (2.49)
(2.49)
Отсюда угловые коэффициенты 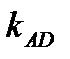 и
и 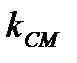 выражаются формулами:
выражаются формулами:
 (2.50)
(2.50)
Пусть уравнение стороны 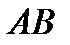 имеет вид
имеет вид
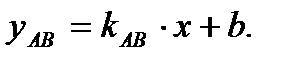 (2.51)
(2.51)
Так как точка 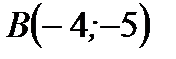 принадлежит прямой
принадлежит прямой 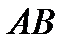 , то координаты этой точки удовлетворяют уравнению прямой
, то координаты этой точки удовлетворяют уравнению прямой 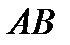 , то есть
, то есть
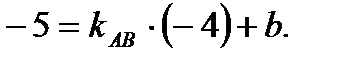 (2.52)
(2.52)
С другой стороны, так как 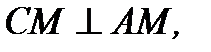 то (см. пример 2.11)
то (см. пример 2.11)
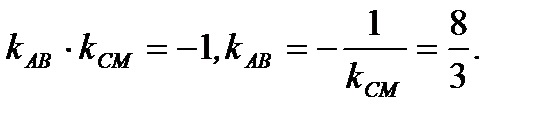 (2.53)
(2.53)
Итак, с учетом (2.51) - (2.53) имеем
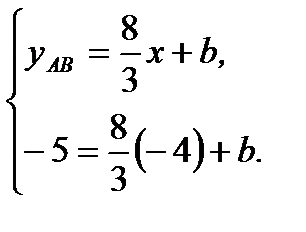 (2.54)
(2.54)
Отсюда
 (2.55)
(2.55)
Аналогично для стороны 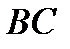 имеем
имеем
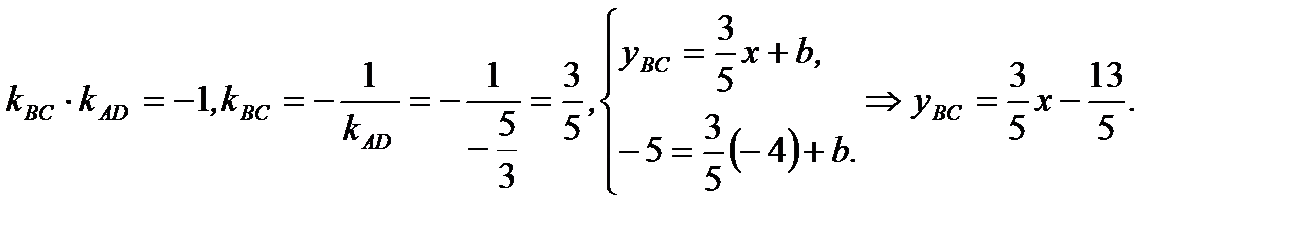 (2.56)
(2.56)
Для составления уравнения стороны 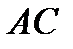 найдем координаты точек
найдем координаты точек 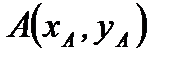 и
и 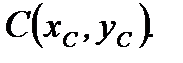 Решая системы уравнений
Решая системы уравнений
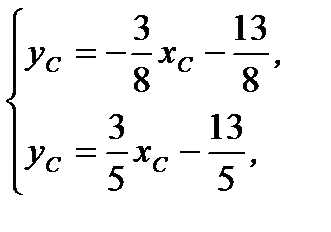
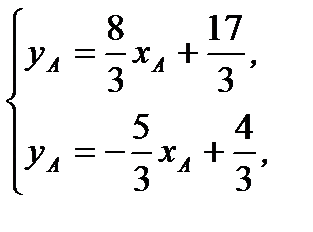 (2.57)
(2.57)
найдем, что 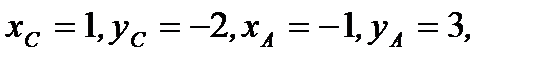 то есть
то есть 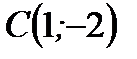 и
и 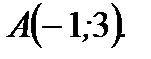 Теперь согласно (2.44) получим
Теперь согласно (2.44) получим 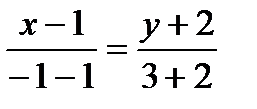 или
или 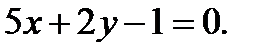
Ответ: 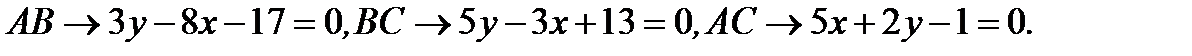
Пример 2.13.Найти расстояние 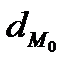 точки
точки 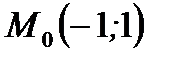 от прямой
от прямой 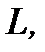 уравнение которой имеет вид
уравнение которой имеет вид 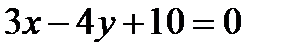 (рис. 2.19).
(рис. 2.19).
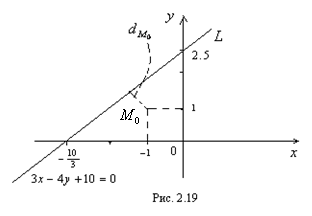
Решение.Для приведения уравнения прямой  к нормированному виду обе части умножим на нормирующий множитель
к нормированному виду обе части умножим на нормирующий множитель 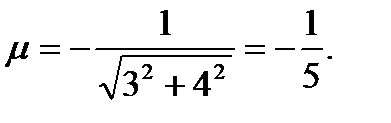 Получим нормированное уравнение прямой
Получим нормированное уравнение прямой  в виде
в виде
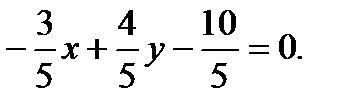
Тогда для отклонения и расстояния точки 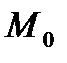 от прямой
от прямой 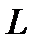 согласно пункту 2.3.2 получим следующие выражения:
согласно пункту 2.3.2 получим следующие выражения:
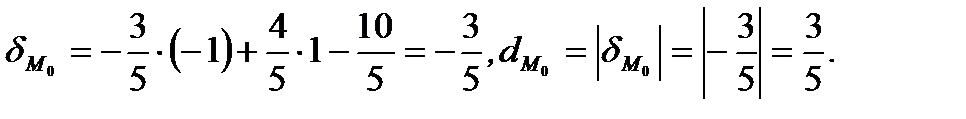
Ответ: 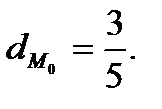
Пример 2.14. (задача экономического характера) Функция издержек 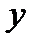 как функция от количества изготовленного товара
как функция от количества изготовленного товара 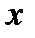 в штуках, линейна, то есть
в штуках, линейна, то есть  Известно, что при
Известно, что при 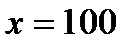 штук
штук 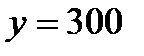 рублей, а при
рублей, а при 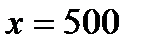 штук
штук 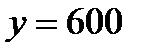 рублей. Найти издержки
рублей. Найти издержки 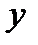 в рублях при изготовлении
в рублях при изготовлении 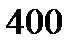 штук товара.
штук товара.
Решение.Согласно условий задачи имеем
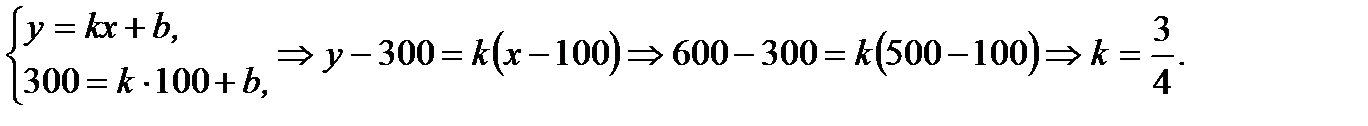
Тогда
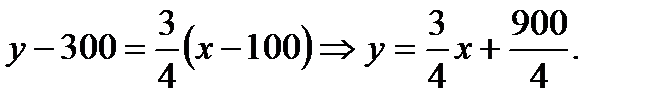 (2.58)
(2.58)
Подставляя в (2.58)  штук, получим
штук, получим
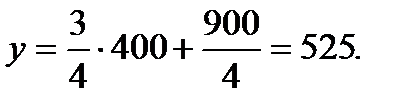
Ответ:525 рублей.
Дата добавления: 2018-11-25; просмотров: 1053;
