ОСНОВНЫЕ ДЕЙСТВИЯ С МАТРИЦАМИ
1. Сложение (вычитание) матриц.Суммой (разностью) двух матриц А = (аij) и B = (bij), имеющих одинаковое количество строк и столбцов, называется матрица С = (сij), элементы которой равны суммам (разностям) соответствующих элементов матриц А и В (сij = аij ± bij).
2. Умножение матрицы на скалярную величину. Произведением матрицы А = (аij) на число α называется матрица, элементы которой получены из элементов матрицы А умножением на число α.
3. Умножение матриц А и В возможно только в том случае, если число столбцов матрицы А равно числу строк матрицы В. При этом элементы матрицы произведения С = А×В определяются следующим образом: элемент сij i-той строки и j-того столбца матрицы С равен сумме произведений элементов i-той строки матрицы А на соответствующие элементы j-того столбца матрицы В.
При
А = (аij), i = 1, 2, ..., n; j = 1, 2, ..., m;
B = (bij), i = 1, 2, ..., р; j = 1, 2, ..., q;
получим
С = А×В = (сij), i = 1, 2, ..., n; j = 1, 2, ..., q, где
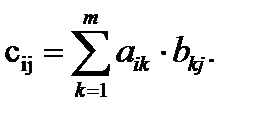
4. Транспонирование матрицы.При транспонировании матрицы строки становятся столбцами, а столбцы строками.
5. Обращение матрицы.Данная операция относится к квадратичным матрицам при условии, что определитель матрицы отличен от нуля (|А| ≠ 0).
Обратной матрицей по отношению к исходной называется матрица, которая, будучи умноженной как справа, так и слева на исходную матрицу дает единичную матрицу:
А×А-1 = А-1×А = 1.
Для обращения матриц небольшой размерности используют метод присоединения матрицы. Согласно этому методу обратная матрица вычисляется по выражению:
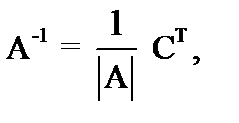
где |А| – определитель исходной матрицы, СТ – транспонированная матрица алгебраических дополнений исходной матрицы:
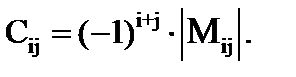
Дата добавления: 2018-09-24; просмотров: 544;
