Верхняя треугольная матрица
ФОРМЫ ЗАПИСИ СИСТЕМЫ ЛИНЕЙНЫЙ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)
В электроэнергетике основные расчеты режимов производят по первому и второму законам Кирхгофа, которые представляются в виде системы линейных алгебраических уравнений (СЛАУ). СЛАУ можно представить следующим образом
1) в развернутой форме
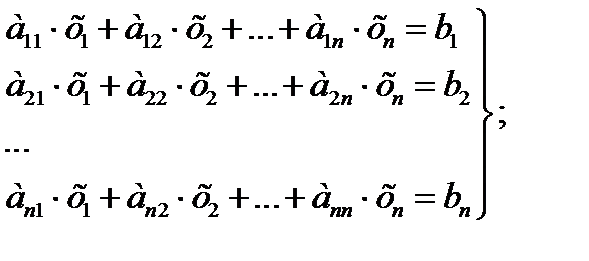
2) в компонентной форме
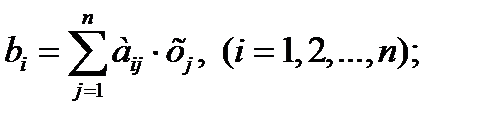
3) в матричной форме
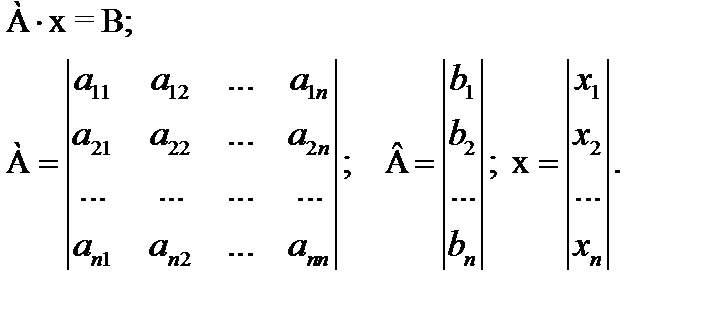
ТИПЫ МАТРИЦ
Матрица – это прямоугольная таблица, имеющая определенное количество строк и столбцов. Строки нумеруются сверху вниз, столбцы – справа налево. На пересечении i-той строки и j-того столбца стоят элементы матрицы. Элементы матрицы могут быть представлены действительными или комплексными числами, символьными переменными, функциями времени, другой матрицей.
Различают следующиевиды матриц:
1. Прямоугольная матрица – количество строк и столбцов матрицы не совпадает (i ≠ j).
2. Квадратная матрица – частный случай прямоугольной матрицы, количество строк и столбцов матрицы одинаково (i = j).
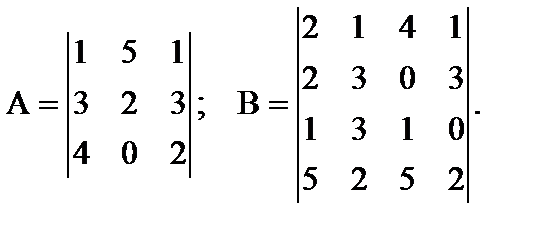
3. Матрица (вектор) строка – количество строк матрицы равно единице, количество столбцов больше единицы (i = 1, j >1).
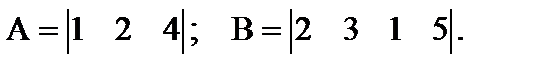
4. Матрица (вектор) столбец – количество столбцов матрицы равно единице, количество строк больше единицы (i > 1, j =1).
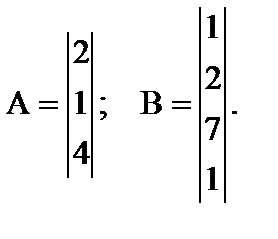
5. Нулевая матрица – все элементы матрицы равны нулю.
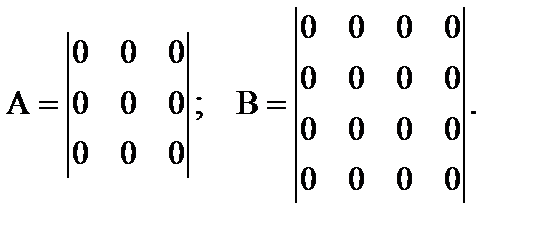
6. Единичная матрица – элементы главной диагонали матрицы равны единице, остальные элементы равны нулю.
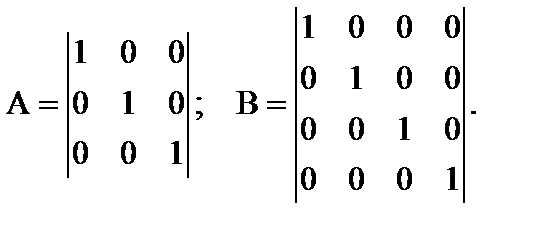
7. Симметричная матрица – элементы матрицы сверху и снизу от главной диагонали имеют одинаковые значения (а12 = а21, а13 = а31 и т.д.).
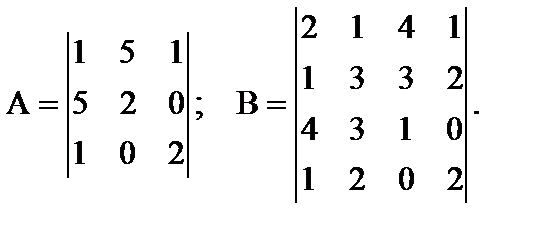
8. Действительная матрица – все элементы матрицы представлены действительными числами.
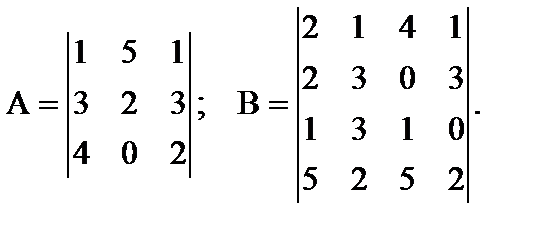
9. Комплексная матрица – некоторые или все элементы матриц представляются комплексными числами.
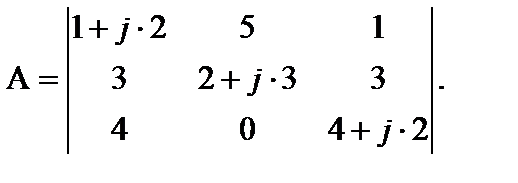
10. Символьная матрица – в качестве элементов матрицы используются символьные переменные или выражения.
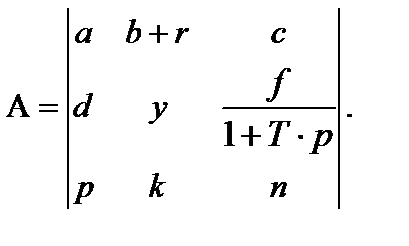
11. Блочная матрица – элементы матрицы представлены другими матрицами
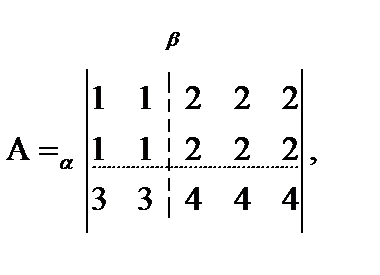
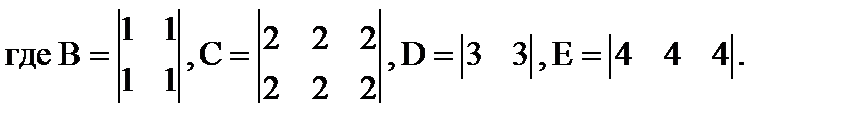
Матрицы могут иметь различную структуру (портрет) – графическое изображение элементов матриц отличных от нуля:
Верхняя треугольная матрица
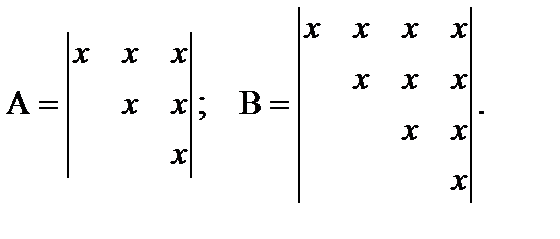
Дата добавления: 2018-09-24; просмотров: 1047;
