Раздел 4. Установившееся движение упругой жидкости и газа в пористой среде

Дифференциальное уравнение установившейся фильтрации упругой жидкости и газа по закону Дарси

Лекция № 19

До сих пор мы рассматривали фильтрацию несжимаемого флюида r=const (без учета уравнения состояния флюидов, т.к. характеристики k, m и m считали постоянными). Эти допущения приводили к простому дифференциальному уравнению фильтрации

DР = 0 и DФ = 0.

Если флюид сжимаем, нужно получить новое дифференциальное уравнение для упругого (сжимаемого) флюида из уравнения неразрывности потока:

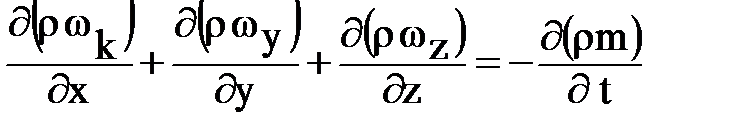
и уравнения движения:

, .

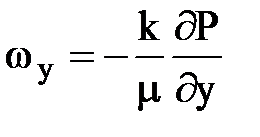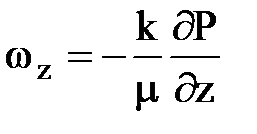Введем функцию Â так, что ее дифференциал

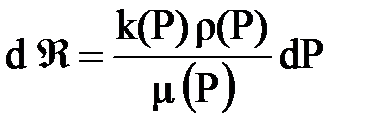или .

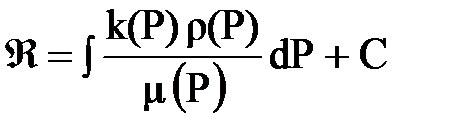Функция Â называется функцией Л.С. Лейбензона. Т.к. Â = Â(х, у, z, t) и Р = Р(х, у, z, t) дифференциал можно переписать

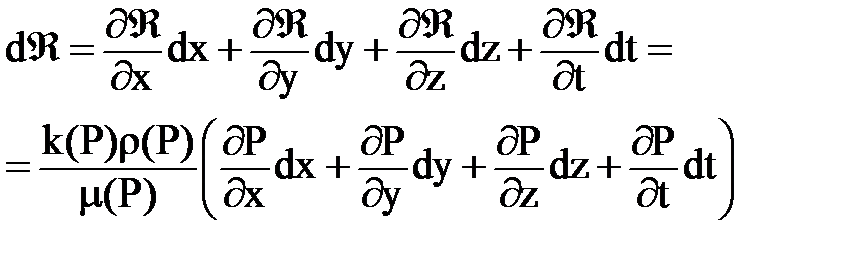, где:

.

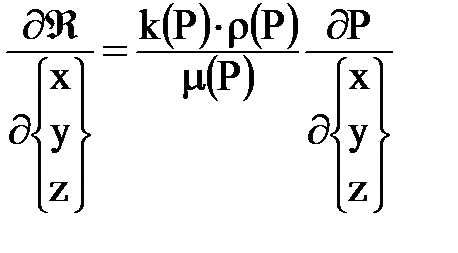Переходя от объемных скоростей (w) к массовым скоростям (rw)

,

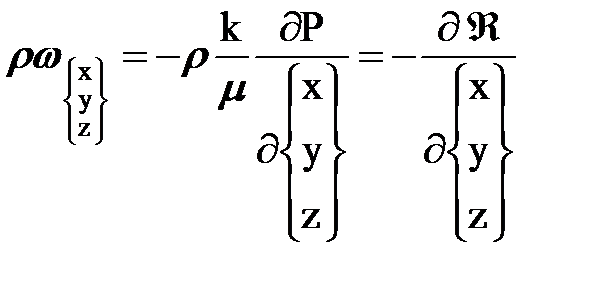и подставляя их в уравнение неразрывности, получим дифференциальное уравнение фильтрации упругого флюида в однородной пористой среде по закону Дарси

.

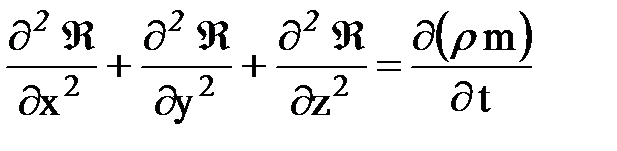В случае установившейся фильтрации

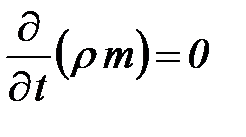и DÂ = 0.

Таким образом, для установившейся фильтрации движения упругого флюида в однородной среде по закону Дарси справедливо уравнение Лапласа, но уже не относительно давления (Р) или потенциала (Ф), а относительно функции Лейбензона Â.

Введение функции Лейбензона в уравнения позволяет установить полную аналогию между установившейся фильтрацией несжимаемого флюида, для которого законы фильтрации нами были уже рассмотрены, и фильтрацией сжимаемого флюида.

В дальнейшем изложении будем считать, что m и k постоянны. Тогда выражение функции Лейбензона упростится:

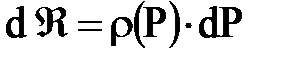и .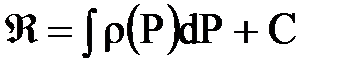

Аналогия заключается в том, что все формулы, полученные для установившейся фильтрации несжимаемого флюида по закону Дарси можно использовать и для установившейся фильтрации сжимаемого флюида в пластах той же геометрии и при тех же граничных условиях, заменив переменные:

Упругий флюид Функция Лейбензона 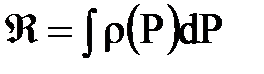Массовый расход флюида 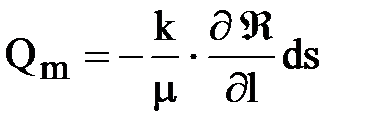массовая скорость фильтрации

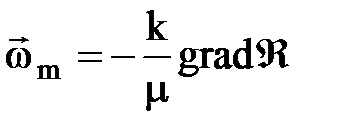
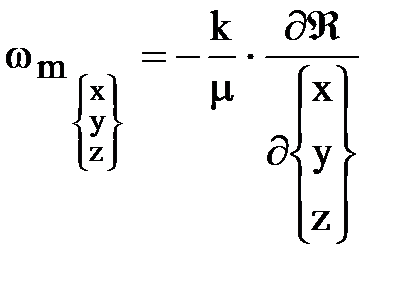
Давление Р

Обменный расход флюида

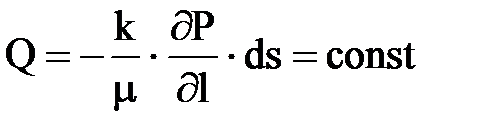
объемная скорость фильтрации

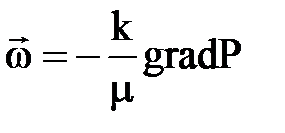
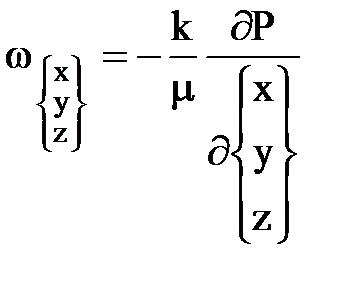
Установившаяся фильтрация упругой жидкости.

Найдем выражение функции Лейбензона для упругой, но слабо сжимаемой жидкости, описываемой уравнениями состояния

.

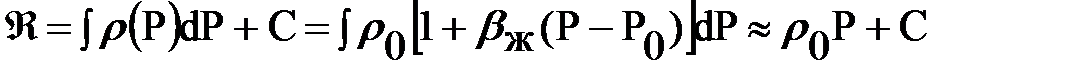Для случая, когда b_ж (Р - Р₀) мало Â 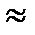r₀Р + С и уравнение фильтрации приводится к виду: .

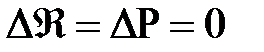Т.е. при установившейся фильтрации упругой (слабосжимаемой) жидкости она в большинстве случаев ведет себя как несжимаемая и можно воспользоваться всеми ранее выведенными формулами. В этом случае метод аналогии параметров применять не надо. Однако, при фильтрации жидкости в пласте с очень высоким пластовым давлением и при большой депрессии надо учитывать ее упругие свойства и рассчитывать функцию Лейбензона и применять метод аналогии.

Рассмотрим применение метода аналогии на конкретных примерах фильтрации упругого газа.

Установившаяся фильтрация газового потока.

В отличие от жидкости газ значительно более сжимаем и на практике функцию Лейбензона и метод аналогий параметров в основном применяют к газовым потокам.

Рассмотрим методику применения на простых моделях фильтрации.