Фильтрационный поток реального газа по двухчленному закону фильтрации к несовершенной скважине.
Вначале составим и запишем уравнение притока реального газа по двухчленному закону фильтрации к совершенной скважине. Оно будет совпадать с аналогичным уравнением для идеального газа, но со множителями 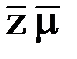 в коэффициентах А и В:
в коэффициентах А и В:
| В¢ |
| А¢ |
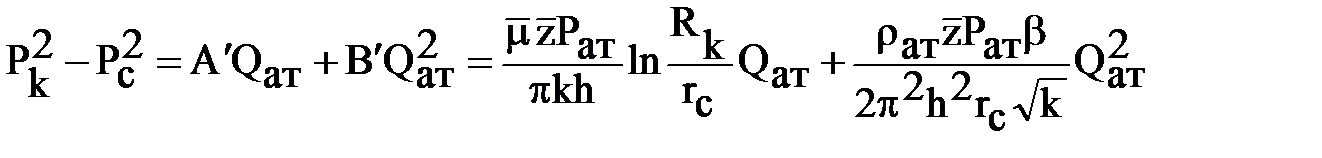 .
.
Несовершенство газовых скважин при соблюдении закона Дарси учитывается так же, как и несовершенство нефтяных скважин, т.е. радиус скважин в формуле дебита заменяется приведенным радиусом, равным
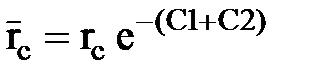 .
.
| Р2 |
| Р1 |
| R1 |
| R2 |
| Rk |
| 2 rc |
| Рис. 20.2 |
| Для расчетов дебитов несовершенных газовых скважин при нарушении закона Дарси можно предложить следующую схему (рис. 20.2). Круговой пласт, в центре которого скважина делится на три круговые зоны. |
Круговой пласт, в центре которого скважина делится на три круговые зоны. Первая зона имеет радиус R1 = (2-3)rс. Здесь имеет место нарушение закона Дарси из-за больших скоростей фильтрации вблизи перфорированных отверстий и проявляется несовершенство скважин по характеру вскрытия.
Вторая область представляет кольцевое пространство (R1<r<R2), где R2 » h. Здесь также имеет место нарушение закона Дарси, проявляется несовершенство скважины по степени вскрытия и применим двухчленный закон фильтрации.
В третьей зоне R2<r<Rк – имеет место плоскорадиальный поток, подчиняющийся закону Дарси. Для этой области можно записать:
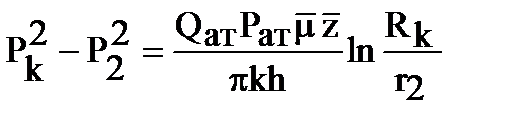 - уравнение Дарси для реального газа.
- уравнение Дарси для реального газа.
Во второй области примем, что толщина пласта переменна и меняется по линейному закону h (r) = a + b r, где a и b определены из условий h=b при r = R1, h (r) = h при r = R2.
Чтобы получить закон движения в этой области надо снова проинтегрировать двухчленный закон фильтрации, подставив в него вместо h выражение h(r). Признав это, получим:
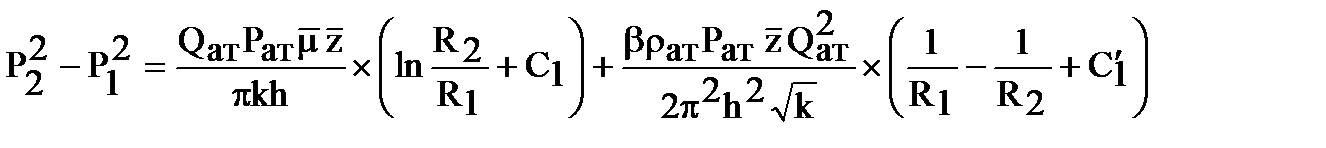 .
.
Здесь С1 и С1¢ - коэффициенты, характеризующие несовершенство скважины по степени вскрытия.
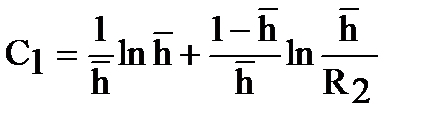 ;
; 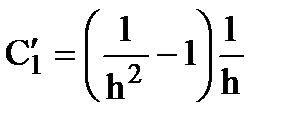 , где
, где 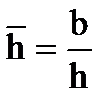 .
.
В первой области, где фильтрация происходит по двухчленному закону и имеет место несовершенная скважина по характеру вскрытия, уравнение движения будет аналогичным, но отличатся постоянными С2 и С2¢.
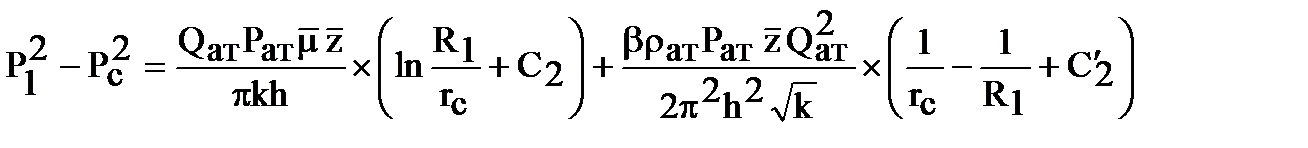 .
.
Коэффициент С2 определяется по специальным графикам В.И. Щурова:
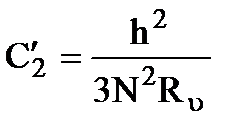 ,
,
где: N – суммарное число перфорированных отверстий, Ru - глубина проникновения пуль в пласт.
Складывая почленно уравнения в трех зонах, окончательно получим:
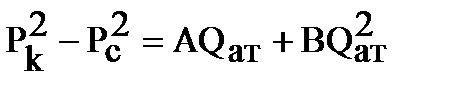 , где
, где
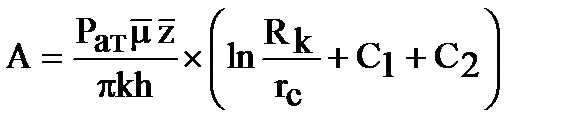 ,
, 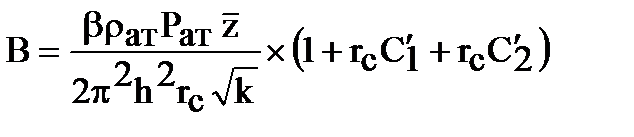 .
.
Раздел 5. Основы моделирования процессов фильтрации нефти, газа и воды
Отметим, что в настоящем пособии изложены наиболее простые для понимания классические положения однофазной фильтрации нефти, воды и газа. За рамками изложения остались сложные вопросы многофазной фильтрации в деформируемых средах, физико-химической гидродинамики, гидродинамики неньютоновской жидкостей и многое другое. Для изучения этих вопросов широко применяется развитый аппарат математической физики, а также методы моделирования процессов фильтрации нефти, газа и воды.
При необходимости дальнейшего самостоятельного углубления знаний по сложным вопросам прикладной гидродинамики необходимы представления об основах моделирования физических процессов вообще и процессов фильтрации подземных флюидов в частности, которые предполагают знание. основ анализа размерностей и теории подобия
2.1. Цели и задачи моделирования фильтрационных процессов
Под моделированием понимается изучение сложного физического процесса при помощи модели, на которой стремятся познать изучаемый процесс с различной степенью детализации для получения необходимых ответов или подтверждения гипотез.
Классический подход к решению сложной проблемы моделирования включает формулировку исходной задачи, описывающей физический процесс, поиск и введение необходимого количества упрощающих предположений, при которых сохраняется существо физического процесса, а переформатированная задача поддается решению теми или иными средствами.
Совершенствование вычислительных средств и систем — необходимая предпосылка для дальнейшего развития моделирования. По мере развития вычислительной техники будут расширяться пределы использования моделирования при решении задач возра стающей сложности.
Приведем примеры постановочных вопросов, решение которых можно получить с помощью моделирования пластовых систем.
Как нужно разрабатывать и эксплуатировать месторождение, чтобы обеспечить оптимальную добычу пластовых флюидов (углеводородных и неуглеводородных)?
Какой наилучший проект увеличения нефтегазоотдачи для данного пласта? Как он должен быть осуществлен?
Какова экономически целесообразная конечная нефтегазоотдача для данного месторождения?
Какие лабораторные и промысловые данные требуются для получения надежных прогнозных результатов? Как пересчитать результаты лабораторного эксперимента на пластовые условия?
Каков наилучший способ вскрытия пласта скважиной?
Из какой части пласта следует отбирать нефть или газ?
Определение цели проводимого исследования и точная постановка более узких (специальных) вопросов — важный этап при выполнении любого исследования на модели.
Основными типы моделей, применяемыми при изучении процессов фильтрации пластовых флюидов при разработки и эксплуатации природных залежей являются: физические, математические, численные и машинные, а также аналоговые модели.
2.2 Виды моделирования процессов фильтрации пластовых флюидов
Физическое моделирование
Физическое моделирование — это замена изучения интересующего явления в природе изучением аналогичного явления на модели меньшего или большего масштаба, обычно в специальных лабораторных условиях. Основной смысл такого моделирования заключается в том, чтобы по результатам опытов с моделями можно было изучить различные характеристики явления в природных условиях. При этом должны выполняться определенные условия (критерии) подобия (геометрического и физического) модельных и натурных процессов. Для этого размеры модели, свойства пласта и флюидов выбирают в лабораторных условиях таким образом, чтобы были выполнены условия геометрического подобия, а соотношения различных сил в пласте и в физической модели были одинаковыми. Большое значение при физическом моделировании фильтрационных процессов имеет теория размерностей и подобия (см. данной главы).
Ввиду чрезвычайной сложности реальных процессов фильтрации в пластовых условиях построить полностью подобные физические модели очень трудно или невозможно. Поэтому в большинстве случаев ограничиваются приближенным моделированием фильтрационных процессов.
Физические модели играют ключевую роль для понимания процессов, происходящих в пласте. Исследования с помощью физических моделей — единственный возможный способ решения практических задач разработки нефтегазовых месторождений в тех случаях, когда математическое описание процессов невозможно, затруднительно или нецелесообразно. Результаты физического моделирования часто используют для проверки и корректировки математических моделей, основанных на различных упрощениях или же гипотезах, справедливость которых требует подтверждения.
Математическое моделирование
Математические модели представляют собой системы математических уравнений, описывающих изучаемый физический процесс на основе некоторых абстракций и допущений, опирающихся на эксперимент и необходимых с практической точки зрения для того, чтобы сделать задачу разрешимой. При моделировании процессов разработки нефтегазовых месторождений эти уравнения в общем виде представляют собой сложные (обычно нелинейные) дифференциальные уравнения в частных производных с соответствующими начальными и граничными условиями.
Любая математическая модель основана на упрощении (идеализации) реального процесса, что позволяет создать расчетные схемы, учитывающие только основные эффекты. В подземной гидравлике моделируют: 1) флюиды (жидкости и газы); 2) породы-коллекторы; 3) геометрическую форму движения; 4) вид процессов, в том числе физико-химических.
Долгое время в подземной гидравлике основными «рабочими» математическими моделями были модели, описывающие установившуюся и неустановившуюся фильтрацию однофазного флюида (несжимаемого и сжимаемого) в однородной пористой среде . Эти модели являются классическими и не утратили своего практического значения и по сей день.
Однако необходимость более полного извлечения нефти, газа и конденсата из пласта, а также проектирование разработки месторождений в осложненных условиях залегания потребовали создания новых, более совершенных математических моделей. В последние годы математическим моделированием стали пользоваться как важнейшим инструментом при проектировании и контроле за разработкой нефтегазовых месторождений. Применение современных ЭВМ позволяет решать гидродинамические задачи, связанные с разработкой, в очень широкой и полной постановке.
Дальнейшее развитие теории и практики разработки месторождений нефти и газа приведет к созданию более совершенных математических моделей, основанных на лучшем знании и понимании гидродинамических и физико-химических процессов, происходящих в залежи при ее разработке, а также связанных с более полным учетом влияния неоднородности коллектора.
Численная и машинная модели
Уравнения, описывающие математическую модель, обычно настолько сложны, что в большинстве случаев их нельзя решить аналитическими методами и необходимо использовать ЭВМ. Чтобы представить дифференциальные уравнения в форме, пригодной для решения на цифровых вычислительных машинах, следует их аппроксимировать и заменить конечно-разностными алгебраическими уравнениями. Численная модель состоит из полученной системы уравнений и построения численного алгоритма их решения.
Машинная модель пластовой системы — это программа или система программ для ЭВМ, составленная с целью решения уравнений численной модели.
Численную и машинную модели можно проверить и даже скорректировать по результатам физического моделирования и данным эксплуатации месторождения, а затем использовать для прогноза показателей разработки месторождения. Таким образом, для понимания сложных пластовых процессов может потребоваться разумное сочетание физического, математического и машинного моделирования.
Аналоговое моделирование
Аналоговое моделирование основано на аналогиях между описанием некоторых фильтрационных процессов с другими физическими явлениями (диффузией, процессом переноса теплоты, электрического тока и т. д.). Основная причина существования аналогий — это сходство уравнений, описывающих различные физические процессы. Аналогия устанавливается на основании того факта, что характеристические уравнения (например, закон Дарси и закон Ома) выражают одни и те же принципы сохранения (массы импульса, энергии, электричества и т. п.), лежащие в основе многих физических явлений. Существующие аналогии позволяют разрабатывать аналоговые модели.
По отношению к пространственным переменным аналоговые модели могут быть либо дискретными, либо непрерывными. В дискретных аналоговых моделях (они эквивалентны конечно-разностным уравнениям численной модели) параметры исследуемой области определяются только в выделенных узловых точках. В непрерывной аналоговой модели (эквивалент дифференциального уравнения математической модели) находит отражение каждая точка прототипа. В обоих типах аналогов время — непрерывная переменная.
Заметим, что в настоящее время в связи с развитием вычислительной техники и численных методов исследования аналоговые модели постепенно вытесняются численными и машинными моделями.
2.3. Основы анализа размерностей и теории подобия
Гидродинамические процессы, характерные для всего комплекса нефтедобычи — от движения нефти в пласте до ее течения по трубопроводам к потребителю, крайне сложны. Во многих случаях недостаточное понимание физики процессов затрудняет не только их изучение с помощью вычислительной техники, но и саму математическую постановку задач. В этих условиях очень важную роль играет применение анализа размерностей и теории подобия, основанного на фундаментальном положении: физические законы не должны зависеть от имеющегося произвола в выборе единиц измерения физических величин. Отсюда выводится, что функции, выражающие физические законы, обладают важным свойством, которое называется обобщенной однородностью. Это свойство позволяет иногда очень существенно упростить определение (расчет, нахождение из опыта) зависимостей, выражающих соответствующие закономерности.
Размерность
Все физические величины выражаются числами, которые получаются в результате измерения. Измерение представляет собой прямое или косвенное сравнение данной величины с соответствующими эталонами — единицами измерения
Единицы измерения физических величин подразделяются на основные и производные. Системой единиц измерения называется совокупность основных единиц измерения, достаточная для измерений явлений рассматриваемого класса. Так, в СИ за основные единицы измерения приняты единицы измерения длины, массы и времени, причем. Остальные единицы измерения, получаемые из основных, называют производными.
Классом систем единиц измерения называется совокупность систем единиц измерения, отличающихся между собой только величиной (но не природой) основных единиц измерения. Для класса систем единиц измерения, к которому относятся системы единиц. СИ, за основные единицы измерения приняты: за единицу длины один метр (м), за единицу массы — один килограмм (кг), за единицу времени — одна секунда (c). Для произвольной системы этого класса соответствующие единицы составляют:
единица длины = м/L;
единица массы = кг/М; (2.1)
единица времени = с/Т.
Здесь L, М, Т — отвлеченные положительные числа, которые показывают, во сколько раз уменьшаются основные единицы длины, массы и времени при переходе от исходной системы, в данном случае СИ, к другой системе рассматриваемого класса. Этот класс обозначается LMT. Обозначение класса систем единиц измерения получается последовательным выписыванием символов величин, единицы измерения которых приняты за основные. Одновременно этими символами обозначают число раз, во сколько уменьшается соответствующая основная единица измерения при переходе от исходной системы, в данном случае СИ, к другой системе данного класса.
Если уменьшить единицу длины в L раз, а единицу времени в Т раз, то, очевидно, новая единица скорости уменьшится по сравнению с исходной в LT-l раз. Следовательно, численное значение всех скоростей возрастет в LT-1 раз. Аналогично и для других величин. Изменение численных значений физических величин при переходе от одной системы единиц измерения к другой в данном классе систем единиц измерения определяется их размерностью. Размерностью физической величины называется функция, определяющая во сколько раз изменяется численное значение этой величины при переходе от исходной системы единиц измерения к произвольной системе внутри данного класса. Размерность величины j принято по предложению Максвелла обозначать [j].
Специально подчеркнем, что размерность определяется для данного класса систем единиц измерения и в разных классах систем единиц измерения размерность одной и той же величины различна. Например, размерность плотности в классе LMT составляет [р]=ML-3. Величины, численное значение которых одинаково во всех системах единиц измерения внутри данного класса, называются безразмерными. Ясно, что размерность безразмерной величины равна единице. Все остальные величины называются размерными.
Размерность любой физической величины всегда представляет собой степенной одночлен, так что, например, в классе LMT размерность величины а представляется в виде: 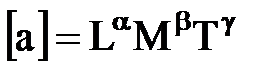 , где a,
, где a, 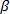 , g — постоянные. Это следует из просто формулируемого, но на самом деле глубокого физического принципа: все системы внутри данного класса равноправны, т. е. среди них нет избранных, чем-то выделенных систем.
, g — постоянные. Это следует из просто формулируемого, но на самом деле глубокого физического принципа: все системы внутри данного класса равноправны, т. е. среди них нет избранных, чем-то выделенных систем.
Говорят, что величины 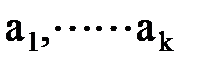 имеют независимые размерности, если размерность ни одной из этих величин нельзя представить в виде произведения степеней размерностей остальных. Например, размерности плотности [r ] = ML-3, скорости [v] = LT-1 и силы [F] — LMT-1 независимы. Напротив, размерности плотности, скорости и давления зависимы: размерность давления [P]=ML-lT-2 равна произведению размерности плотности на квадрат размерности скорости. Ни одна из величин с независимыми размерностями
имеют независимые размерности, если размерность ни одной из этих величин нельзя представить в виде произведения степеней размерностей остальных. Например, размерности плотности [r ] = ML-3, скорости [v] = LT-1 и силы [F] — LMT-1 независимы. Напротив, размерности плотности, скорости и давления зависимы: размерность давления [P]=ML-lT-2 равна произведению размерности плотности на квадрат размерности скорости. Ни одна из величин с независимыми размерностями  не может быть безразмерной: размерность безразмерной величины, равная единице, равна произведению размерностей остальных величин, какими бы они ни были, в нулевой степени.
не может быть безразмерной: размерность безразмерной величины, равная единице, равна произведению размерностей остальных величин, какими бы они ни были, в нулевой степени.
Для дальнейшего существенен следующий факт: всегда можно перейти внутри класса (не обязательно MLT) от исходной системы к некоторой другой системе данного класса так, чтобы любая величина из набора величин с независимыми размерностями  , скажем a1изменила численное значение в произвольное число А раз, а все прочие величины остались неизменными.
, скажем a1изменила численное значение в произвольное число А раз, а все прочие величины остались неизменными.
Действительно, в выбранном классе систем единиц измерения Р, Q,…….,.R. ( отличном от класса MLT) размерности величин  имеют вид:
имеют вид:
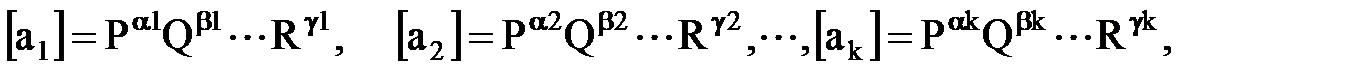
причем для каждого члена ряда, хотя бы один из показателей степени не равен нулю. Следовательно, по определению размерности при переходе от исходной системы единиц к той системе единиц, которую мы ищем, числа Р, Q, . . .R (неизвестные множители) должны удовлетворять соотношениям
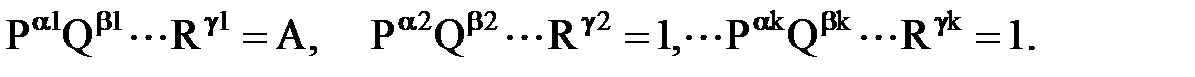
Логарифмируя соотношения, получаем для логарифмов неизвестных переходных множителей In Р, In Q, . . lnR. систему линейных алгебраических уравнений:

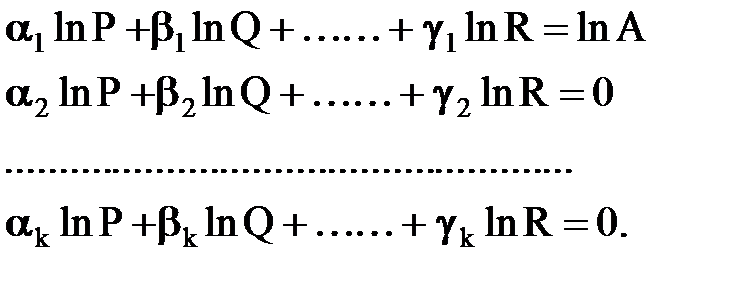
которая, как нетрудно видеть, всегда разрешима. Это свойство используется при построении анализа размерностей.
2.3.1 Анализ размерностей (p-теорема)
Во всяком физическом исследовании, теоретическом или экспериментальном, находятся зависимости одних величин, характеризующих явление, от других. Дело всегда сводится, таким образом, к отысканию одного или нескольких соотношений вида
a=f (a1,………ak,ak+1,……..an)
Здесь а — определяемый параметр (функция); а1……. аn — величины, которые считаются заданными, они называются определяющими параметрами (аргументами). Разбиение определяющих пара можно сделать так, чтобы параметры a1,………ak имели независимые раз  мерности, а размерности параметров ak+1,……..an выражаются в виде произведения степеней размерностей параметров a1,………ak
мерности, а размерности параметров ak+1,……..an выражаются в виде произведения степеней размерностей параметров a1,………ak
 где
где 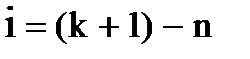
Такое разбиение можно сделать всегда. В частных случаях может быть k = n, если размерности всех определяющих параметров независимы, или k = 0, если все определяющие параметры безразмерны. В общем случае 0<k<n.
Размерность определяемой величины а должна выражаться в виде произведения степеней размерностей величин a1,………ak. Следовательно, должны существовать числа (показатели степеней, которые можно подобрать) р, . . . , г, такие, что

Если бы это было не так, размерности величин (a, a1,………ak) были бы независимыми. Тогда, согласно свойству, доказанному в предыдущем разделе, можно было бы, изменяя систему единиц измерения внутри данного класса, менять величину а во сколько угодно раз, оставляя неизменными значениях всех определяющих параметров, чего не может быть, если список определяющих параметров полон.
В результате анализа размерностей доказывается, что искомая функция
a=f (a1,………ak,ak+1,……..an),
определяющая ту или иную физическую закономерность, обладает свойством обобщенной однородности, т. е. представляется через функцию меньшего числа безразмерных параметров: П1, , Пi, Пn-k, где 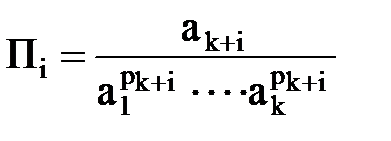
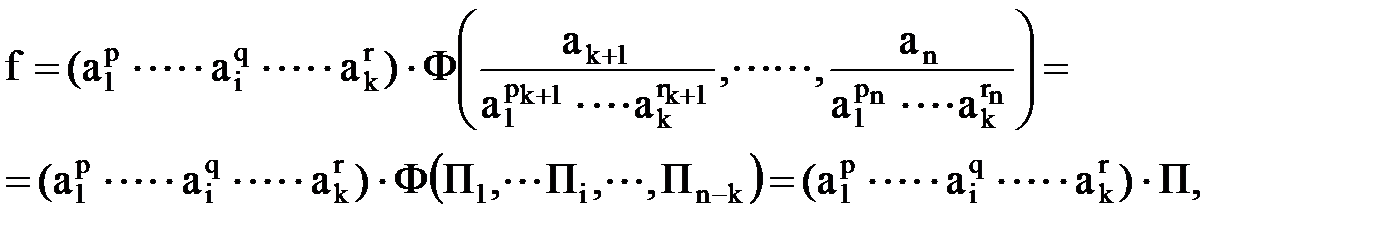
Эти факты составляют содержание основного утверждения анализа размерностей, так называемой p-теоремы.
Важность этой теоремы связано с тем, что в формуле первый сомножитель 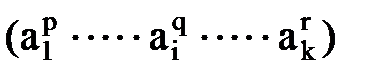 , определяющий размерность искомой функции сформировывается в явном виде, а второй сомножитель
, определяющий размерность искомой функции сформировывается в явном виде, а второй сомножитель
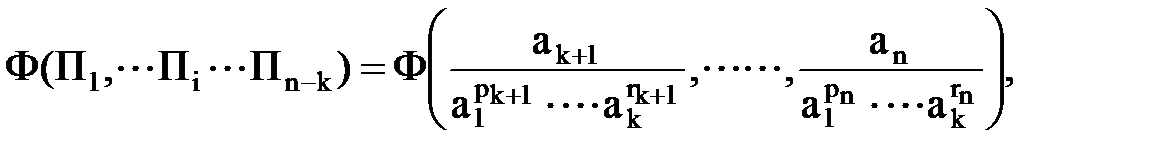 является уже функцией меньшего чиcла (n-k) безразмерных параметров Пi. Для определения зависимости той или иной величины а от каждого определяющего параметра надо измерить или вычислить функцию f, скажем при 10 значениях соответствующего аргумента. Тогда для определения функции f надо провести всего 10n измерений или вычислений.
является уже функцией меньшего чиcла (n-k) безразмерных параметров Пi. Для определения зависимости той или иной величины а от каждого определяющего параметра надо измерить или вычислить функцию f, скажем при 10 значениях соответствующего аргумента. Тогда для определения функции f надо провести всего 10n измерений или вычислений.
После применения анализа размерностей дело сводится к определению функции Ф от (п—k) безразмерных аргументов Для нахождения этой функции уже достаточно 10n-k опытов или вычислений, т. е. в 10k раз меньше. Мы приходим к важному выводу: трудоемкость определения искомой зависимости благодаря применению анализа размерностей сокращается на столько порядков, сколько среди определяющих параметров величин с независимыми размерностями.
2.3.2.Теория подобия
В подземной гидравлике очень часто прибегают к моделированию явлений, в том числе к физическому моделированию процесса фильтрации пластовых флюидов. Для правильного моделирования основным является понятие физического подобия явлений.
Понятие физического подобия, естественно, обобщает понятие подобия геометрического. Например, два треугольника подобны, если они отличаются только численными значениями параметров — длин сторон, а углы при вершинах для обоих треугольников одинаковы. Аналогично физические явления называются подобными, если они отличаются только численными значениями размерных определяющих параметров и притом так, что для них величины соответствующих безразмерных параметров совпадают.
В связи с принятым определением подобных явлений величины П1, , Пi, Пn-k введенные в предыдущем разделе называются параметрами подобия.
Рассмотрим теперь некоторое явление, которое предполагается моделировать, будем называть его натурным. Потребуем, чтобы модельное явление, которым мы хотим воспользоваться для определения нужных характеристик натурного, было подобным натурному. Следовательно, для обоих явлений имеет место зависимость определяемой характеристики а от определяющих параметров a1,………an:
a=f (a1,………ak,ak+1,……..an)
При этом функция f для обоих явлений одна и та же, поскольку они подобны, хотя численные значения определяющих параметров a1,………an и определяемого параметра а могут различаться. Запишем теперь искомую функцию определяемого параметра в форме, вытекающей из p-теоремы
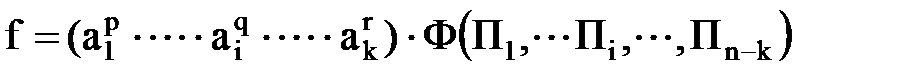
Как сказано выше, для обеспечения подобия явления в натуре и на модели должны совпадать соответствующие безразмерные параметры описывающего его процесс уравнения. Это означает, что
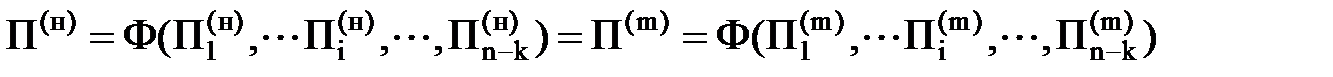
и 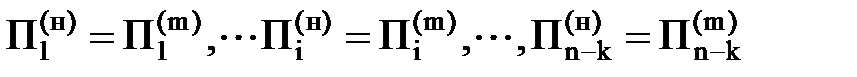
Последние условия называют критериями подобия. Здесь верхним индексом (н) обозначены величины, соответствующие натурному явлению, а индексом (т) — величины, относящиеся к модельному явлению. Используя анализ размерностей, находим для обоих явлений
Критерии подобия, равенство параметров подобия для модельного и натурного явлений, указывают, как надо выбирать остальные определяющие параметры Раскрывая эти условия получим
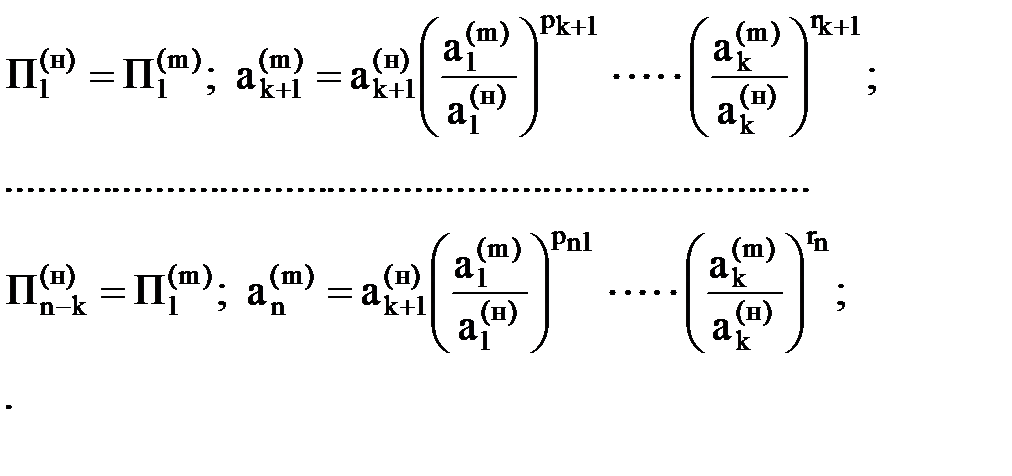
Приведенные простые определения и утверждения исчерпывают содержание анализа размерностей и теории подобия.
Дата добавления: 2017-02-20; просмотров: 891;
