Плоскорадиальный фильтрационный поток реального газа по закону Дарси.
Если пластовое давление выше 10 МПа, а депрессия не слишком мала (рс/рк £ 0.9), то уравнение состояния газа значительно отличается от идеального газа и плотность газового потока определяется не по закону Клапейрона-Менделеева, а по формуле: 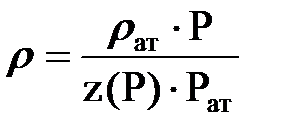 , где: z(P) – коэффициент сверхсжимаемости при соответствующем давлении.
, где: z(P) – коэффициент сверхсжимаемости при соответствующем давлении.
Кроме того, для высоких пластовых давлений нужно учитывать зависимость вязкости от давления 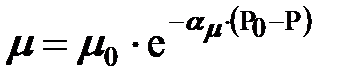 или
или 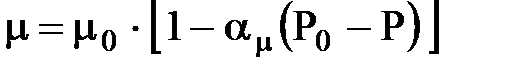 .
.
Проницаемость будем считать постоянной.
Функцией Лейбензона в этом случае будет выражение:
 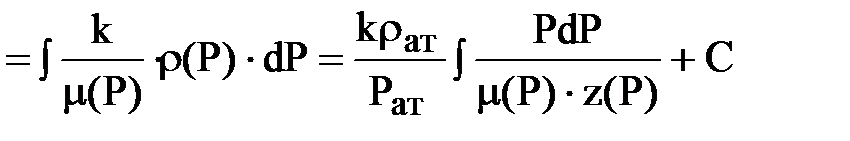 .
.
Найдем дебит скважины при плоскорадиальном движении, используя аналогию между установившейся фильтрацией несжимаемой жидкости и газа. Для чего заменим в формуле Дюпюи объемный дебит массовым, а 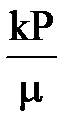 - значениями функции Лейбензона:
- значениями функции Лейбензона:
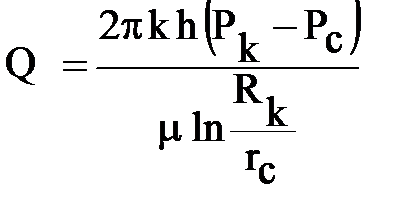 ®
® 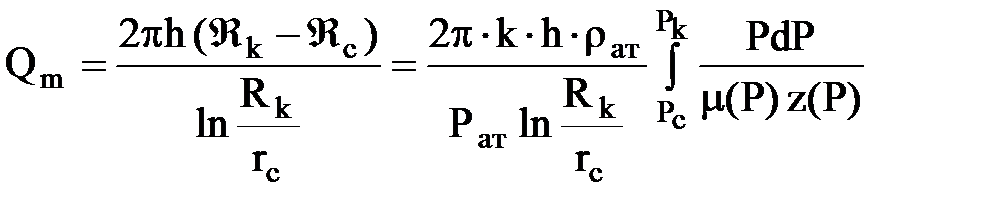
где: 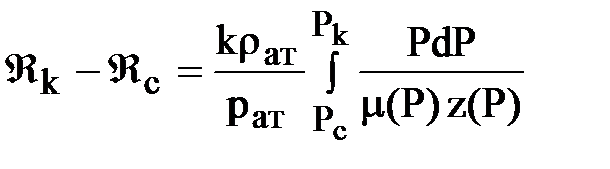 (приращение функции Лейбензона заменяем определенным интегралом).
(приращение функции Лейбензона заменяем определенным интегралом).
Затем получаем объемный дебит газа при атмосферном давлении
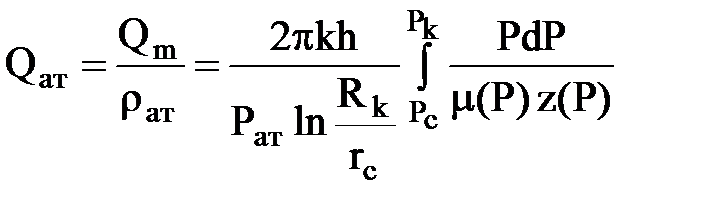 .
.
Существует несколько способов вычисления интеграла в формуле. Наиболее распространен следующий способ. По графикам зависимости z(Р) и m(Р) определяют значения z(Рc) = zс, z(Рк) = zк и m(Рс) = mс, m(Рк) = mк, а переменные под знаком интеграла z и m заменяются их средними значениями из значений на контуре и в скважине:
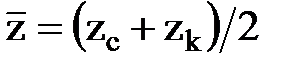 ;
; 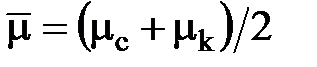 .
.
Тогда интеграл легко вычисляется и объемный дебит, приведенный к атмосферному давлению принимает вид:
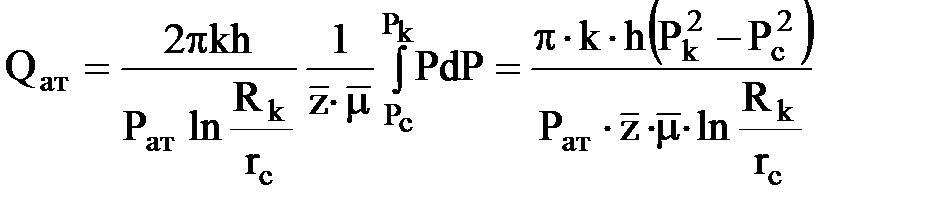 .
.
Нетрудно видеть, что выражение дебита реального газа отличается от выражения идеального газа множителями 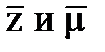 в знаменателе.
в знаменателе.
Второй способ заключается в вычислении определенного интеграла при подстановке в него функций.
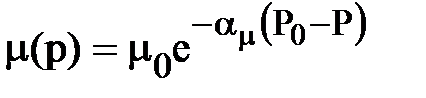 ,
, 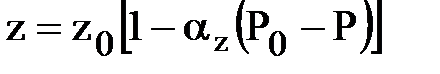 .
.
Дата добавления: 2017-02-20; просмотров: 1502;
