Прямолинейно-параллельный фильтрационный поток идеального газа
Предварительно найдем функцию Лейбензона для идеального газа, используя уравнение состояния
,
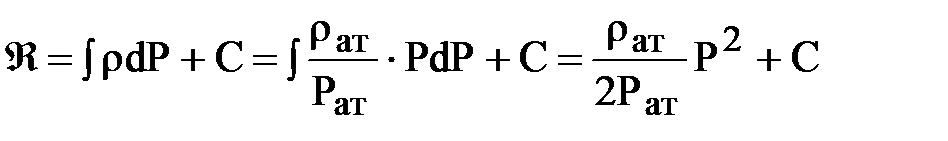где: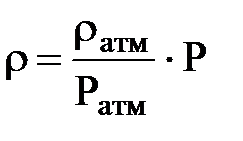 
- функция состояния r = r (Р).
Для нахождения фильтрационных характеристик газового потока используем метод аналогий параметров между потоком несжимаемой жидкости и течением сжимаемого газа.
Находим распределение давления в потоке идеального газа:
.
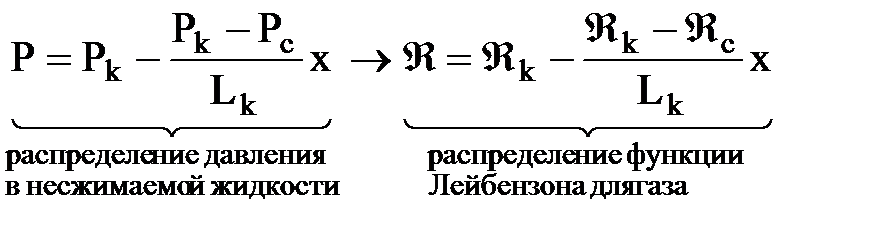Подставляя в последнюю формулу значение функции Лейбензона получим:
.
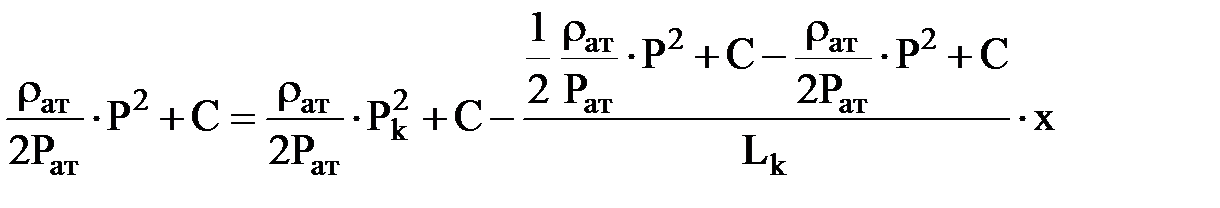Отсюда находим изменение давления в пласте:
.
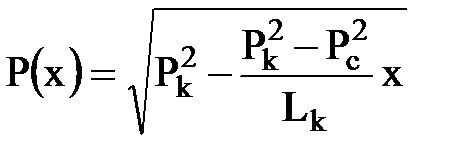Находим градиент давления по такой же схеме:
,
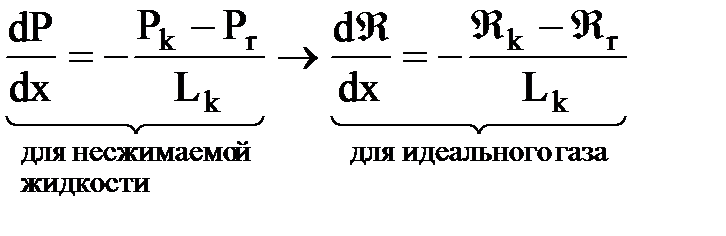подставляем сюда функции 
и 
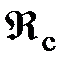, а также производную функции
,
получим:
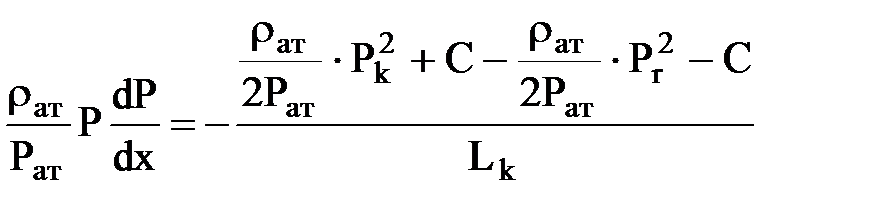, откуда 
.
|
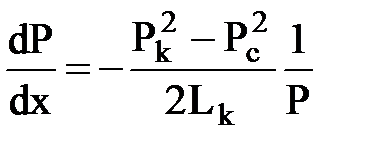Как видно, в отличие от несжимаемого флюида изменение давления в плоскопараллельном потоке подчиняется нелинейной зависимости, а gradP не остается постоянным и возрастает при приближении к галерее. Распределение давления и его градиента в потоке показаны на рис. 19.1.
| Рис. 19.1 |
Объемный расход газа находим из формулы массового дебита, где вместо Р фигурирует функция Лейбензона Â:
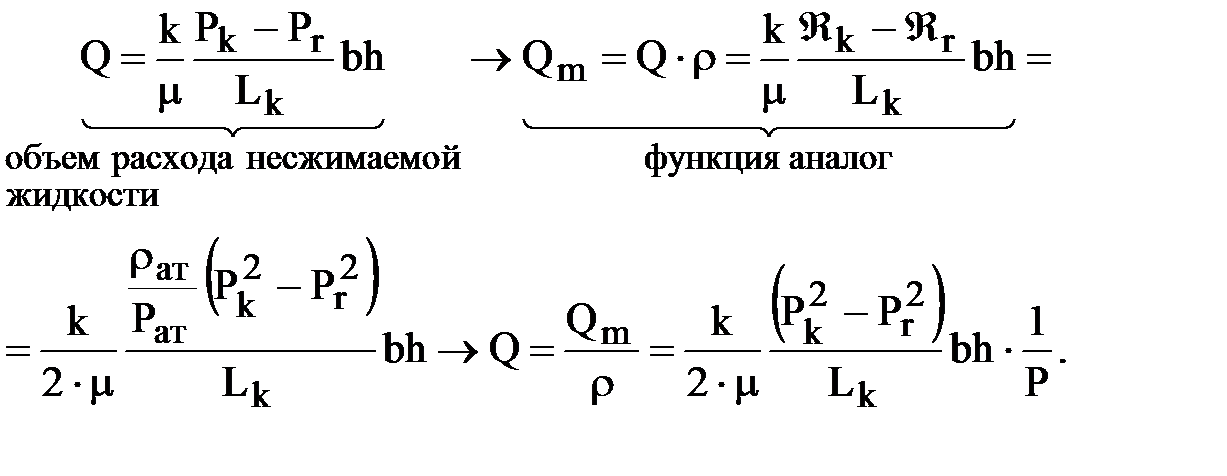
Таким образом, дебит газа зависит от давления (а значит от координаты x).
Скорость фильтрации газа получим. разделив объемный дебит на площадь сечения пласта:
.
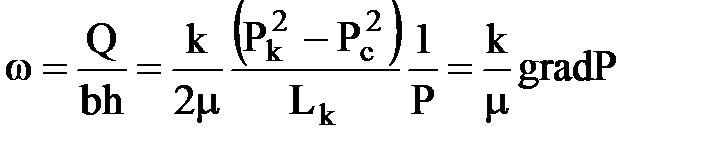Значит, график скорости фильтрации аналогичен графику градиента. Физически возрастание скорости в фильтрационном потоке объясняется расширением газа при снижении давления.
Средневзвешенное давление газа в пласте определим прямым расчетом:
; 
; 
,
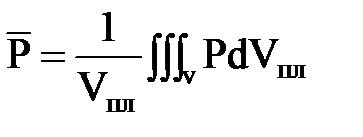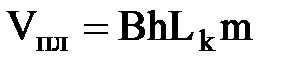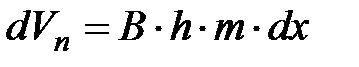интегрируем по переменной x от радиуса скважины до контура Lк , получим:
.
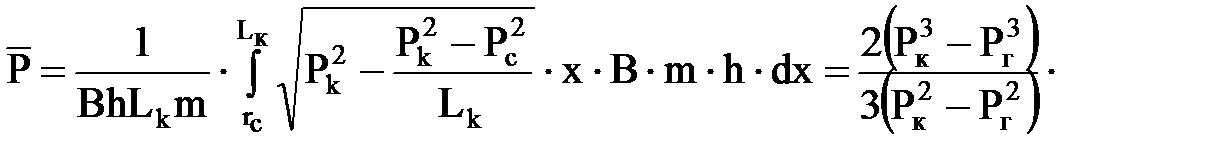Дата добавления: 2017-02-20; просмотров: 2426;