Плоскорадиальный фильтрационный поток идеального газа по закону Дарси.
Характеристики потока в такой модели найдем по методу аналогий, зная характеристики подобного потока несжимаемой жидкости и выражение функции Лейбензона.
Распределение пластового давления газа в модели.
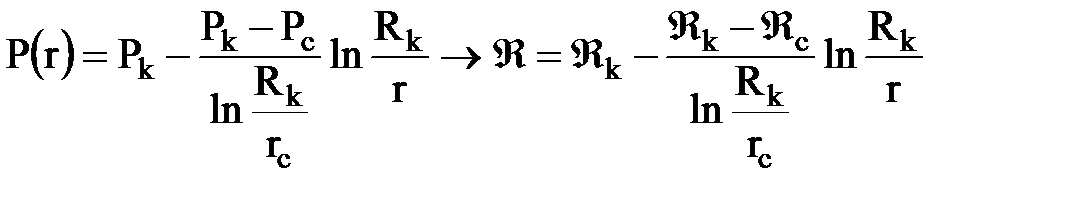 .
.
Подставляя значения функции Лейбензона 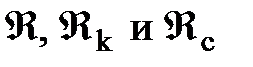 , получим
, получим
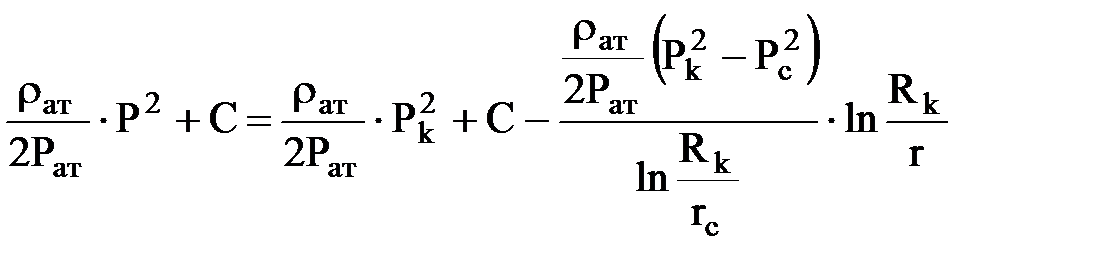 ,
,
откуда 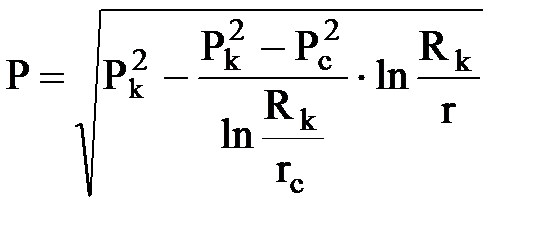 .
.
На рисунке 19.2 видно, что в газовом потоке по сравнению с жид-костным, воронка депрессии охватывает меньшую область возмущения, но характеризуется более высокими градиентами давления вблизи скважины.
| газ |
| жидкость |
| Rk |
| Pc |
| r |
| Рис. 19.2 |
Градиент давления в пласте
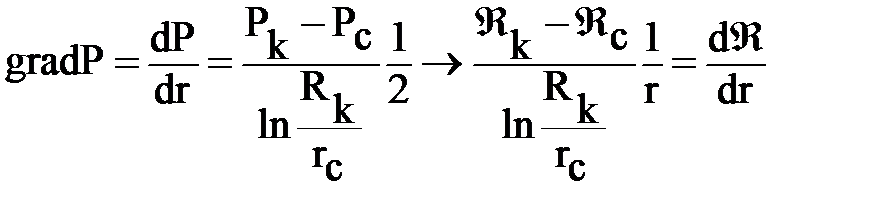 ;
;
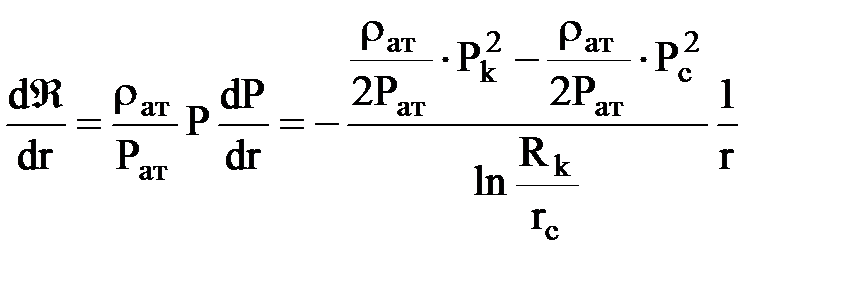 ; и
; и 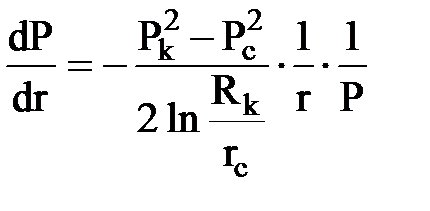 ;
;
т.о., градиент давления вблизи скважины резко возрастает как за счет уменьшения координаты r, также и падения давления Р.
Дебит газовой скважины получим из формулы Дюпюи, подставляя вместо объемного дебита (Q) массовый (Qm,), а вместо давления (P) функцию Лейбензона (Â):
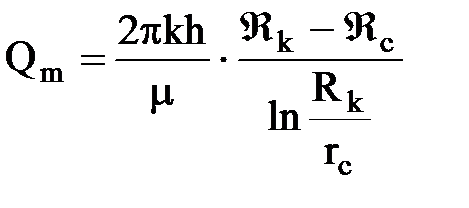 или объемный дебит будет:
или объемный дебит будет:
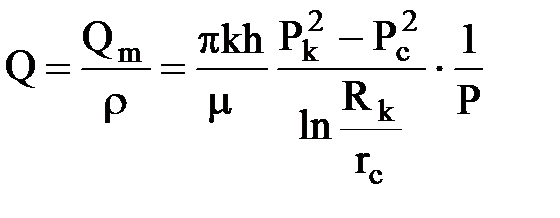 , где:
, где: 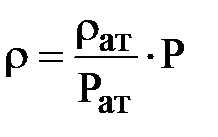 .
.
Имея ввиду неразрывность массового потока 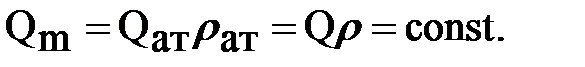 , объемный дебит, измеряемый на устье скважины при атмосферном давлении, будет:
, объемный дебит, измеряемый на устье скважины при атмосферном давлении, будет:
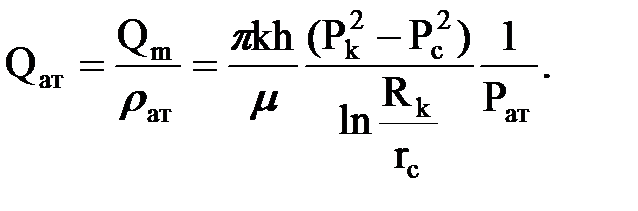
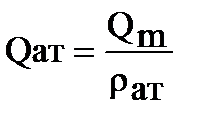
|
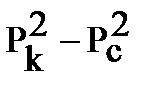
|
| Рис. 19.3 |
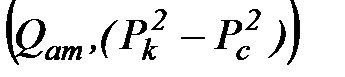 - имеет вид прямой линии (рис. 19.3). Скорость фильтрации получим, разделив дебит на площадь сечения потока фильтрации (S = 2prh)
- имеет вид прямой линии (рис. 19.3). Скорость фильтрации получим, разделив дебит на площадь сечения потока фильтрации (S = 2prh)
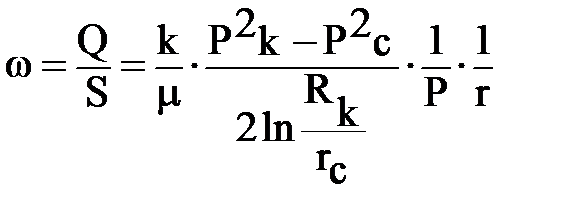 ,
,
Комментарий к скорости фильтрации тот же, что и к градиенту давления. Средневзвешенное по объему порового пространства пластовое давление
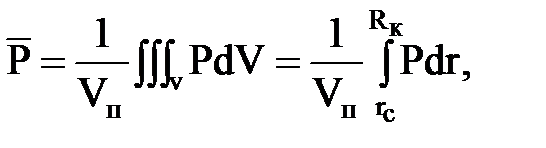
где: 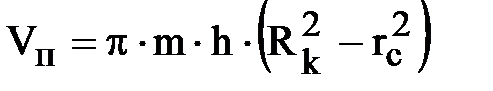 ;
; 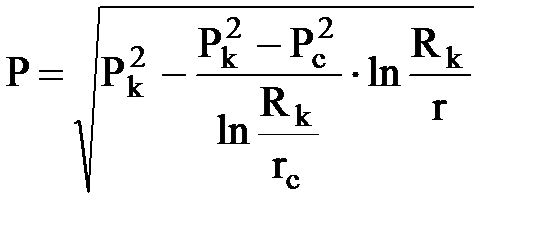 ;
;
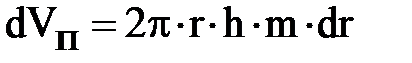 , подставляя и интегрируя, получим:
, подставляя и интегрируя, получим:
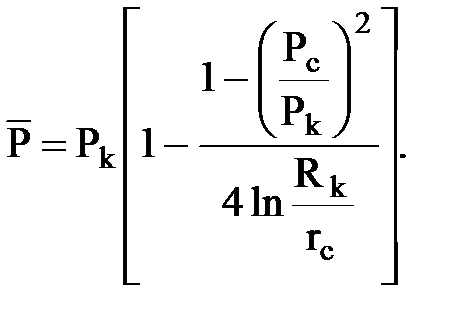
Расчеты показывают, что значение 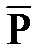 при различных (Рk, Рc, Rk и rc) близко к контурному
при различных (Рk, Рc, Rk и rc) близко к контурному 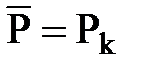 . Физически это объясняется локальным характером и значительной крутизной воронки депрессии при притоке газа к скважине. Средневзвешенное
. Физически это объясняется локальным характером и значительной крутизной воронки депрессии при притоке газа к скважине. Средневзвешенное 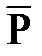 используется при определении запасов газа в пласте, а также для приближенного расчета гидродинамических характеристик; замена его контурным давлением значительно упрощает расчеты.
используется при определении запасов газа в пласте, а также для приближенного расчета гидродинамических характеристик; замена его контурным давлением значительно упрощает расчеты.
Дата добавления: 2017-02-20; просмотров: 1435;
