Решение плоских задач фильтрации методом теории комплексного переменного
Лекция №18
Этим методом некоторые классы задач можно решать проще и эффективнее, чем другими методами. Для рассмотрения основ метода напомним основные положения функции комплексного переменного.
Функцией F(z) комплексного переменного z=x+iy называется функция F(z) = M+jN где M = M (x, y), N = N (x, y) – функции двух действительных переменных. Необходимым и достаточным условием, чтобы F(z) была аналитической функцией комплексного переменного z, является выполнение соотношения Коши - Римана
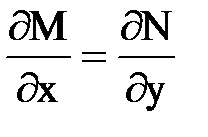 ;
; 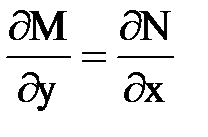 .
.
При выполнении этих условий F(z) имеет производную d/dz независимую от направления интегрирования в области z, а функции M (x, y) и N (x, y) являются гармоническими, т.е. удовлетворяют условию Лапласа
DM = DN = 0.
Рассмотрим плоский несжимаемый поток фильтрационной жидкости.
Компоненты скорости этого потока:
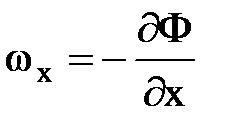 ,
, 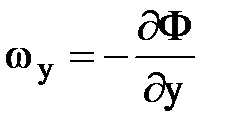 ,
,
удовлетворяют уравнению неразрывности 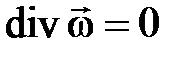 . Из этого уравнения следует, что
. Из этого уравнения следует, что
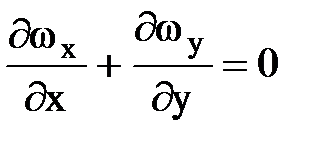 ;
;
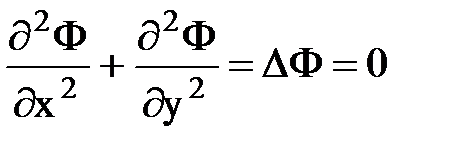 ,
,
а во-вторых, что существует некоторая функция Y(х, у) такая, что
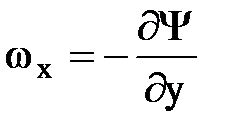 ,
, 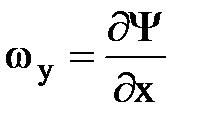 и
и  .
.
Значит 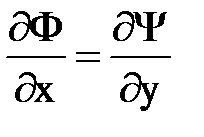 , а
, а 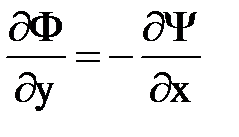 и условия Коши-Римана выполняются. В этом случае функции Ф и Y образуют функцию комплексной переменной , называемую функцией течения или комплексным потенциалом
и условия Коши-Римана выполняются. В этом случае функции Ф и Y образуют функцию комплексной переменной , называемую функцией течения или комплексным потенциалом
F(z) = Ф (х, у) + jY(x, y),
где: Y(x, y) – называют функцией тока. Раскроем ее физический смысл.
На плоскости z рассмотрим отрезок линии тока 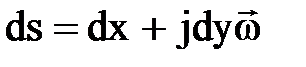 , т.к. вектор скорости
, т.к. вектор скорости  совпадает с направлением касательной и ds можно записать:
совпадает с направлением касательной и ds можно записать:
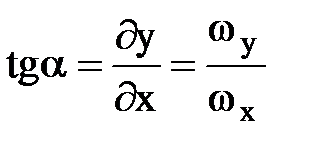 или
или 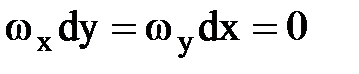 ,
,
 - полный дифференциал функции Y(x, y).
- полный дифференциал функции Y(x, y).
Отсюда: dY = 0 и Y = const.
Это означает, что Y=const. описывает уравнение линий тока. Изменяя константу, получим полное семейство линий.

Рис. 18.1
Можно показать, что эквипотенциали и линии тока взаимноортогональны в любой точке М (рис 18.1). Производная 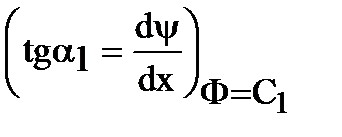 является касательной к эквипотенциали Ф = С1, но так как вдоль нее приращение потенциала нет DФ =
является касательной к эквипотенциали Ф = С1, но так как вдоль нее приращение потенциала нет DФ = 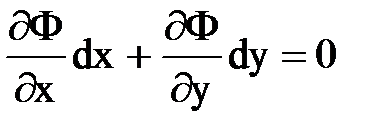 , то
, то 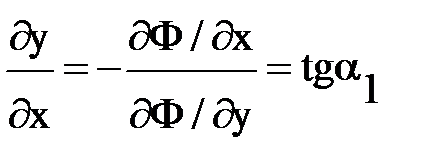 ; аналогично вдоль линии тока Y = С2 имеем
; аналогично вдоль линии тока Y = С2 имеем 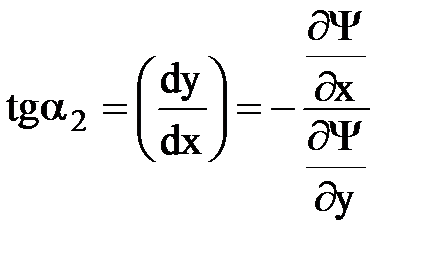 .
.
Рассмотрим произведение
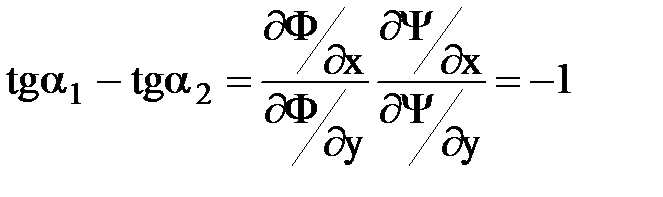
(по условию Коши-Римана 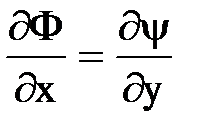 и
и 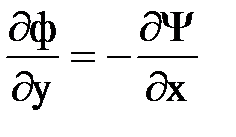 ), а это может иметь место, если
), а это может иметь место, если  .
.
Определим физический смысл функции тока Y. Возьмем две линии тока и соединим их линией АВ (рис.18.2 и 18.3). Проекция вектора 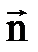 : nx = cos (n, x) = (sin q), ny = cos q.
: nx = cos (n, x) = (sin q), ny = cos q.

|

|
| Рис. 18.2 Рис. 18.3 |
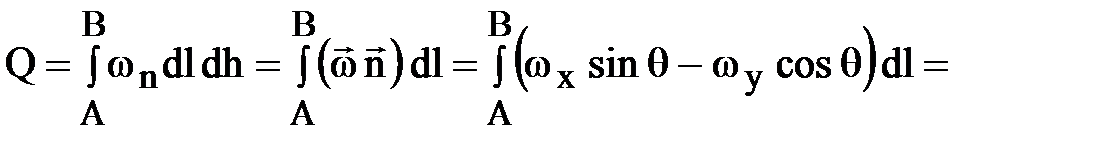
Найдем расход через сечение АВ (считая h = 1):
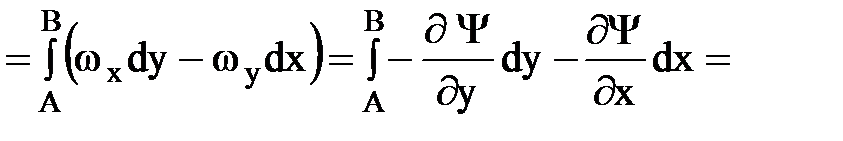
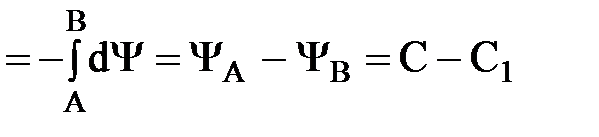
таким образом, расход между двумя линиями тока равен разности значений функции тока на этих линиях.
Найдем производную 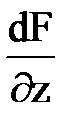 , зависящую от направления дифференцирования. Выберем направление дифференцирования в плоскости z, совпадающее с направлением оси х
, зависящую от направления дифференцирования. Выберем направление дифференцирования в плоскости z, совпадающее с направлением оси х
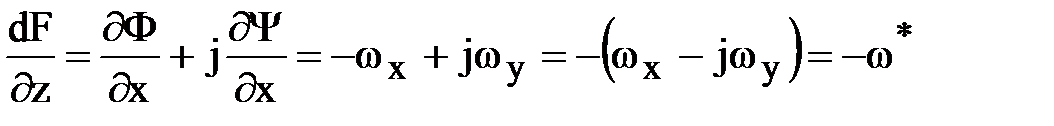 ,
,
т.е. производная комплексной функции равна значению комплексно-сопряженной скорости с обратным знаком. Модуль ее производной 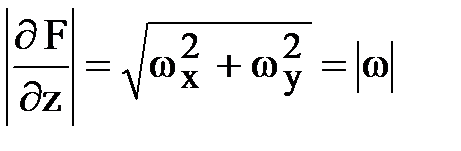 равен модулю скорости движения жидкости.
равен модулю скорости движения жидкости.
Найдем закон движения частицы жидкости вдоль линии тока Y-const. Пусть dx и dy проекции элемента пути dS вдоль линии тока. Можно записать:
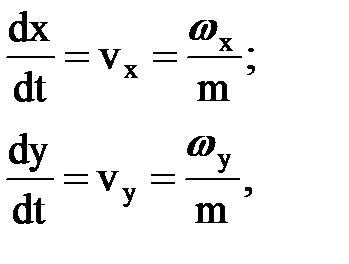
где: m – пористость, или
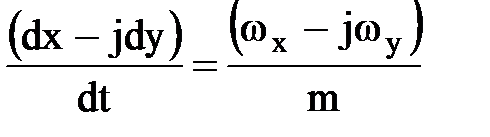 ,
,
по dx – jdy = dz*, значит
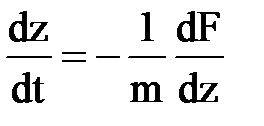 или
или 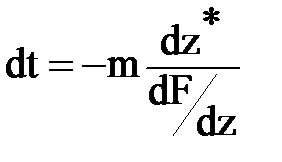 , откуда
, откуда 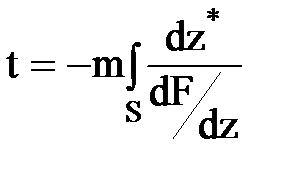 .
.
Отметим в заключение обзора, что комплексные потенциалы потоков F(z)=Ф(х, у)+j Y(x, y) можно суммировать по принципу суперпозиции, т.к. функции Ф и Y удовлетворяют уравнению Лапласа.
2. Рассмотрим примеры применения функций комплексного переменного для решения простейших задач на плоскости.
а) Прямолинейно-параллельный поток.
Для прямолинейно-параллельного потока комплексным потенциалом является функция F(z)=az+b, где а и b – комплексные постоянные а=а1+jа2, b=b1+jb2. (Для плоских задач функция получается заменой в реальном потенциале действительного аргумента х или rна комплексную переменную z). Вид функции при этом сохраняется. Для плоскопараллельного потока, например, потенциал тока 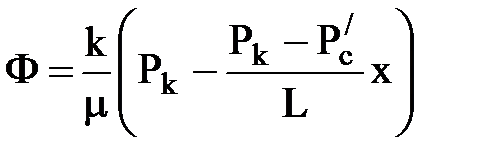 ,
,
а ее комплексный аналог F= аz+b; для точечного стока 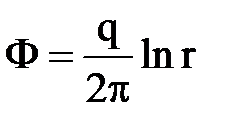 , а комплексный потенциал
, а комплексный потенциал 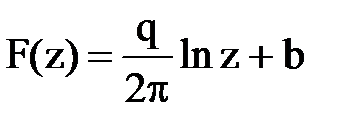 и т.д.).
и т.д.).
Разделим в 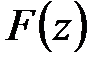 действительную и мнимую части
действительную и мнимую части
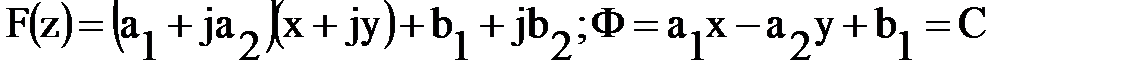
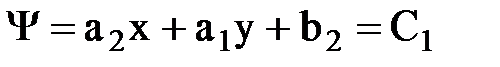 .
.
Эквипотенциали представляют прямые линии с угловым коэффициентом  , а линии тока также прямые с угловым коэффициентом
, а линии тока также прямые с угловым коэффициентом 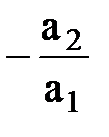 . Они взаимно перпендикулярны, т.к.
. Они взаимно перпендикулярны, т.к. 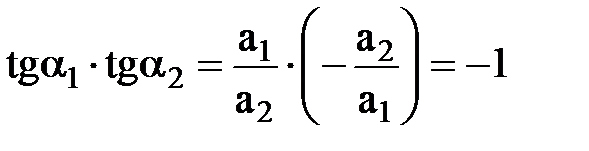 .
.
Компоненты скорости фильтрации равны соответственно
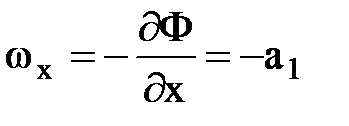 ,
, 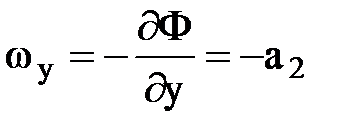 и
и 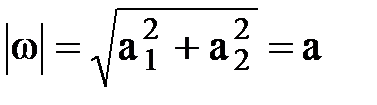 ,
,
т.е. движение происходит с постоянной скоростью. Это следует и из другого ее определения: 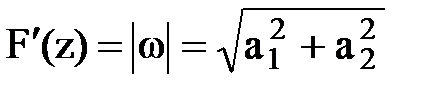 .
.
б) Точечный сток, расположенный в начале координат, имеет комплексный потенциал 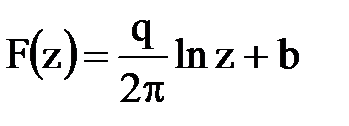 , где q – расход на единицу толщины пласта (при q>0 – источник, q<0 – сток). Разделим действительную и мнимую части, используя полярную систему координат:
, где q – расход на единицу толщины пласта (при q>0 – источник, q<0 – сток). Разделим действительную и мнимую части, используя полярную систему координат:
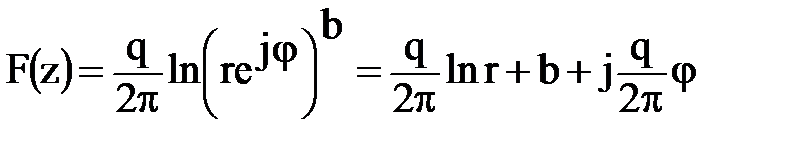 .
.
Откуда следует, что 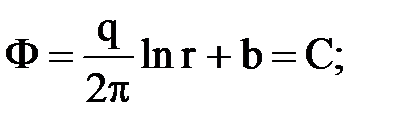
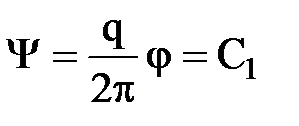 .
.

|
| Рис. 18.4 |
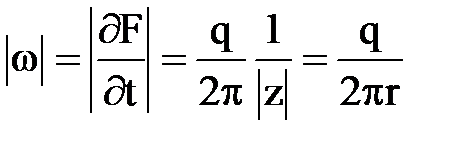 .
.
Из этой формулы следует, что в начале координат F(z) имеет особую точку и поэтому не будет аналитической (производная обращается в бесконечность).
| Рис. 18.4. |
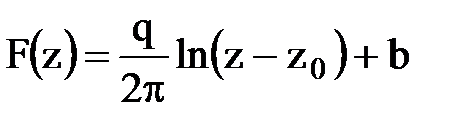 .
.
При переходе к полярным координатам полагают z-z0 = rejj. Здесь особой точкой будет точка z0.
в) Работа в пласте равно дебитного стока и источника. Поместим их в точки х = а, х = -а, у = 0.
Комплексный потенциал стока в этом случае 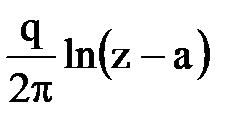 , а источника
, а источника 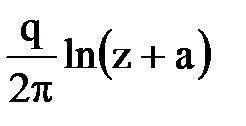 .
.
Суммарный потенциал по принципу суперпозиции
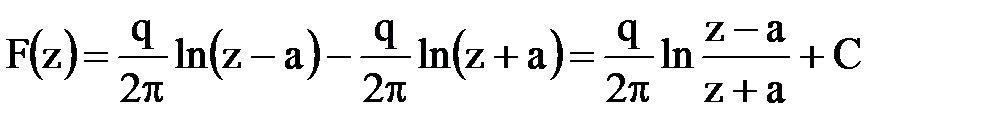 .
.
Выведем уравнения эквипотенциалей и линий тока. Возьмем произвольную точку z = x + jy (точка М) на плоскости течения (рис. 18.5). Обозначим
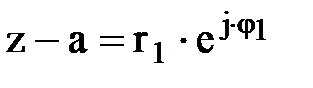 и
и 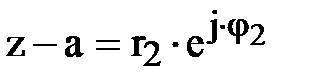 .
.

|
| Рис. 18.5 |
| Рис. 18.5. |
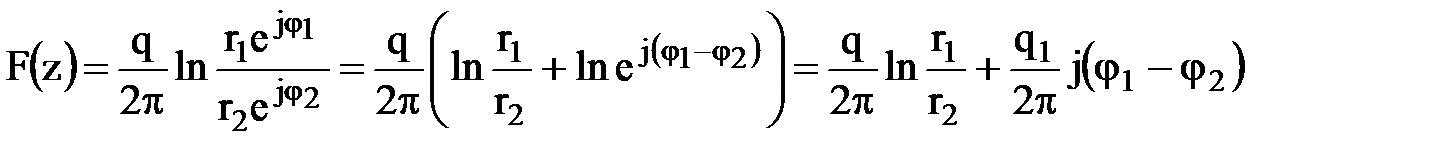 .
.
После чего уравнения эквипотенциалей и линий тока запишутся:
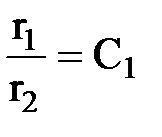 или
или 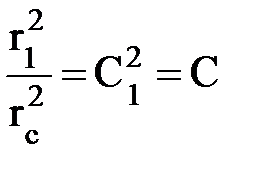 ,
, 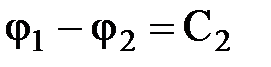 .
.
В уравнении эквипотенциальной линии перейдем к декартовым координатам.  ,
, 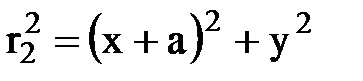 ,
,
тогда 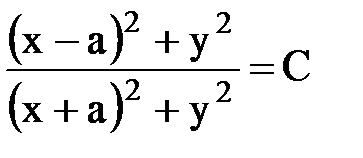 Þ
Þ 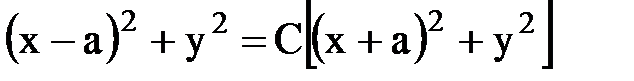 Þ
Þ
Þ 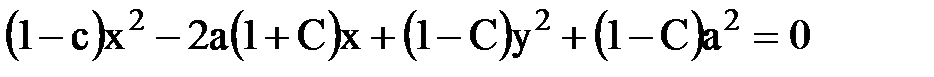 Þ
Þ
Þ 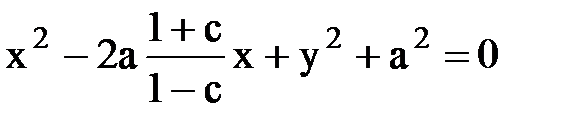 , где с¹1.
, где с¹1.
Прибавим и вычтем выражение 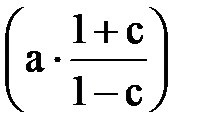 , чтобы получить квадрат разности:
, чтобы получить квадрат разности:
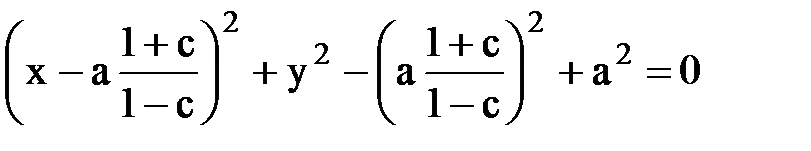 Þ
Þ 
 .
.
Это уравнение окружности с центром в точке х0 = 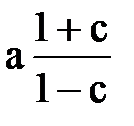 , у0 = 0 и радиусом
, у0 = 0 и радиусом 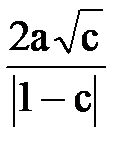 . Изменяя постоянную константу С от нуля до 1, получим семейство окружностей в правой полуплоскости, не концентричных со скважиной-стоком, с увеличивающимися радиусами. Константа С = 1 соответствует окружности с бесконечным радиусом, т.е. оси у. В левой полуплоскости при х<0 картина зеркальная. Для нее полагают 1<c<¥.
. Изменяя постоянную константу С от нуля до 1, получим семейство окружностей в правой полуплоскости, не концентричных со скважиной-стоком, с увеличивающимися радиусами. Константа С = 1 соответствует окружности с бесконечным радиусом, т.е. оси у. В левой полуплоскости при х<0 картина зеркальная. Для нее полагают 1<c<¥.
Преобразуем аналогичным образом уравнение линий тока (рис.18.5) 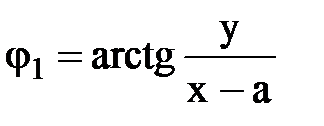 ;
; 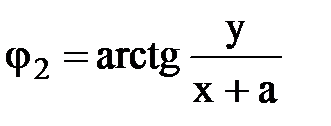 ;
;
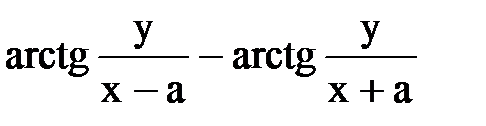
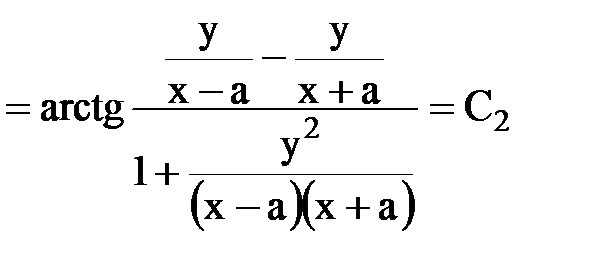 .
.
Последнее выражение приводится к виду 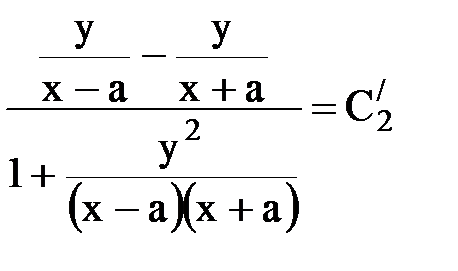 Þ
Þ
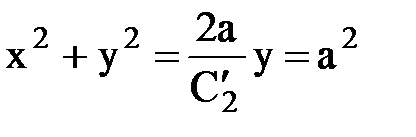 Þ Þ
Þ Þ 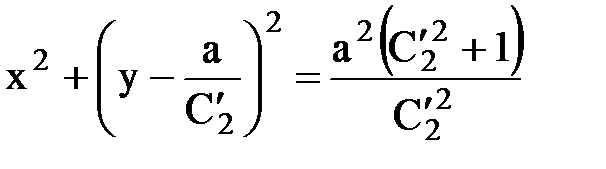 .
.
Таким образом, линии тока также окружности, но с центром на оси у (х0 = 0, y0 = 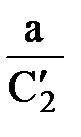 ) и радиусами
) и радиусами 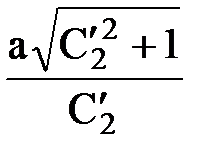 , проходящие через сток (х = а) и источник (х = - а).
, проходящие через сток (х = а) и источник (х = - а).
В заключение найдем скорости фильтрации, через значения производной комплексной функции
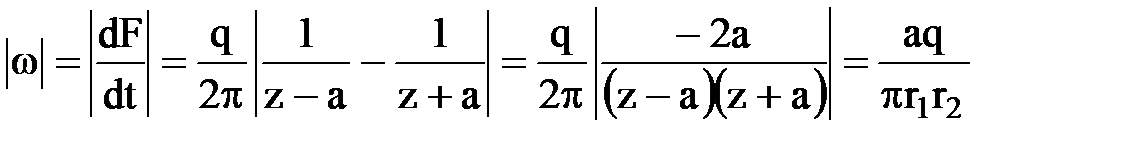 .
.
Если рассмотреть только правую половину плоскости течения 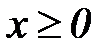 , то комплексный потенциал пары сток - источник описывает приток к одному стоку, расположенному в точке х = а, у = 0 вблизи прямоугольного контура питания, которым является ось у (т.е. эквивалентный результат метода изображения стока вблизи прямоугольного контура).
, то комплексный потенциал пары сток - источник описывает приток к одному стоку, расположенному в точке х = а, у = 0 вблизи прямоугольного контура питания, которым является ось у (т.е. эквивалентный результат метода изображения стока вблизи прямоугольного контура).
При помощи принципа суперпозиции с использованием функции комплексного переменного можно решать различные задачи. Например, можно показать, что комплексный потенциал скважины, эксцентрично расположенный в круговом пласте с эксцентриситетом d: 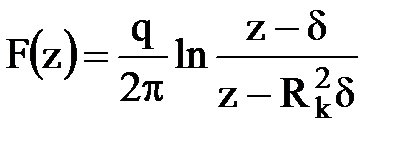 ,
,
а комплексный потенциал кольцевой батареи из m скважин радиуса R1 в круговом пласте радиуса Rk 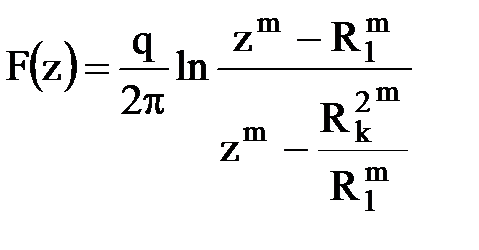 .
.
Дата добавления: 2017-02-20; просмотров: 773;
