Интерференция скважин.
Лекция № 15
3.8.1 Общие положения
| åQi |
| n |
| Рис. 15.1 |
Введем некоторые новые понятия:
- точечный сток – точка на плоскости пласта, поглощающая жидкость; сток можно рассматривать как гидравлически совершенную скважину бесконечно малого радиуса в пласте единичной мощности (рис. 15.2 (а));
- точечный источник – точка, выделяющая жидкость (модель нагнетательной скважины) (рис. 15.2 (б)).
| Рис. 15.2 |
| сток |

|
| а) |
| источник |
| б) |
Найдем потенциал Ф точечного стока на плоскости. Т.к. точечный сток является моделью добывающей скважины и течение вокруг него плоскорадиальное, то скорость фильтрации можно выразить через удельный дебит (дебит скважины на единицу мощности)
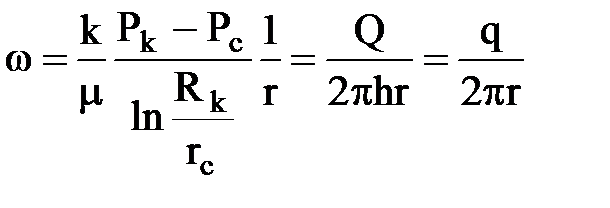 ,
,
где: w - скорость фильтрации; Q- объемный дебит; q = Q/h - удельный дебит жидкости.
Связь потенциала скорости фильтрации с вектором скорости
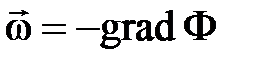 , где:
, где: 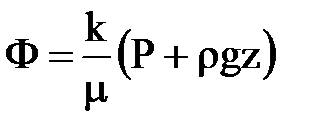 .
.
Если направление касательной 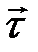 к траектории движения совпадает с направлением скорости фильтрации и градиента давления, тогда:
к траектории движения совпадает с направлением скорости фильтрации и градиента давления, тогда:
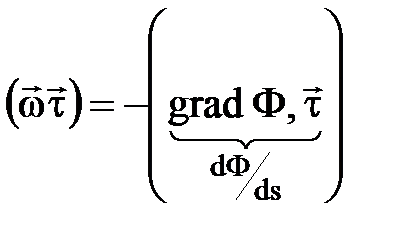 или
или 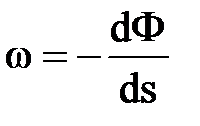 ,
,
но для плоскорадиального течения 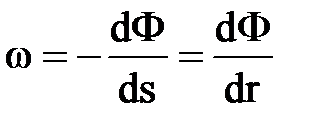 .
.
Отсюда 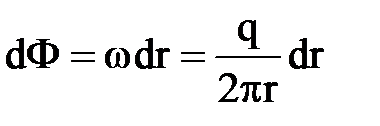 и после интегрирования
и после интегрирования 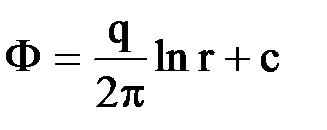 .
.
Потенциал в точке r = 0 и r = ¥ теряет смысл. Эквипотенциальные линии представляют собой семейство окружностей r = const.
Для точечного источника выражение потенциала аналогичное, но q<0.
Найдем теперь потенциал точки стока не в плоскости, а в пространстве. Рассуждения аналогичные, что и для стока на плоскости, но движение вблизи такого рода стока радиально-сферическое, поэтому
 ,
, 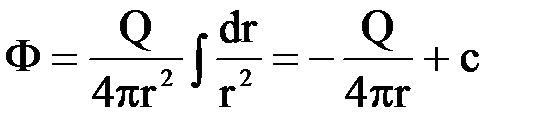 .
.
Для потенциала точечного источника знак дебита меняется на противоположный.
Модель точечного стока в пространстве будет в дальнейшем использована для решения различных задач притока жидкости к гидравлически совершенным и несовершенным скважинам.
Отметим, что метод стоков и источников находит применение не только для решения задач фильтрации, но также задач теплопроводности, электричества и магнетизма.
Вернемся к вопросам интерференции. Математический смысл метода суперпозиции заключается в том, что если имеется несколько источников фильтрационных потоков от скважин с потенциалами Ф1(x, y, z), Ф2 (x, y, z) … Фn (x, y, z), каждый из которых удовлетворяет уравнению Лапласа DФi = 0, то сумма их 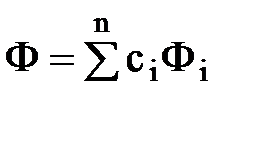 - также является его решением. Подбирая сi можно удовлетворить всем граничным условиям.
- также является его решением. Подбирая сi можно удовлетворить всем граничным условиям.
Гидродинамический смысл метода суперпозиции состоит в том, что давления (потенциалы) в любой точке пласта, вызванные работой каждой скважины (добывающей и нагнетательной) алгебраически суммируется, а вектор суммарной скорости фильтрации частицы жидкости в данной точке находится как геометрическая сумма векторов скоростей, вызванных работой каждой скважины.
Пусть на неограниченной плоскости расположены n стоков, потенциал каждого из них в точке М равен Ф(i)M, где: i = 1,2….n (рис. 15.3).
 , , 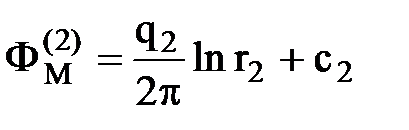 , ,
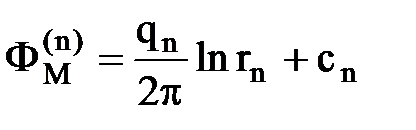 . .
|
| Рис. 15.3 |

Каждая из функций потенциалов Ф(i)M удовлетворяет уравнению Лапласа, тогда и суммарный потенциал в точке М
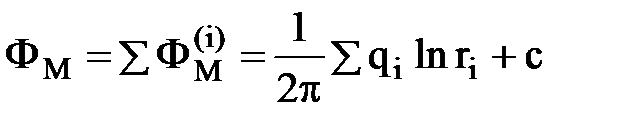 , где
, где 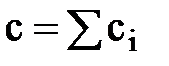 ,
,
также является его решением. Физически это означает, что фильтрационные потоки накладываются друг на друга. В этом и заключается принцип интерференции. Вектор суммарной скорости фильтрации  в точке М равен геометрической сумме векторов скоростей (рис. 15.3).
в точке М равен геометрической сумме векторов скоростей (рис. 15.3).
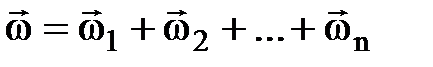 ,
,
где: 
 .
.
Метод суперпозиции можно использовать не только в пластах, имеющих круговой контур питания, или бесконечно больших пластах, но и имеющих контур питания иной формы или непроницаемую границу. В этом случае для выполнения граничных условий приходится вводить фиктивные точечные стоки и источники. При этом решение задач в таких пластах сводится к учету одновременной работы и реальных и фиктивных источников. Метод называется методом отображения стоков и источников.
Рассмотрим, изложенные здесь принципы суперпозиции, при решении некоторых задачах, имеющих практическое применение в разработке нефтегазовых месторождений.

|
3.8.2. Приток жидкости к группе скважин в пласте с удаленным контуром питания.
Пусть в горизонтальном пласте толщиной h расположена группа скважин А1, А2… Аn, c радиусами rci, работающая с различными забойными потенциалами Фci:
| Рис. 15.4 |
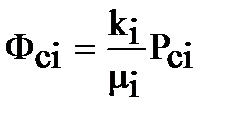 ,
,
где: 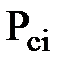 - давление на забое скважин.
- давление на забое скважин.
Так как контур питания достаточно удален от всех скважин, можно приближенно считать, что их расстояния до точек контура одинаковы и равны Rk (рис. 15.4).
Потенциал в любой точке пласта, в том числе на забое любой скважины (Фсi), определяется как сумма потенциалов всех источников:
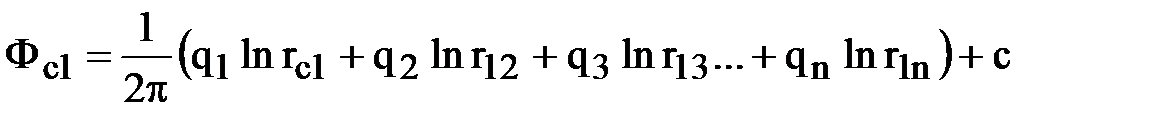 ,
,
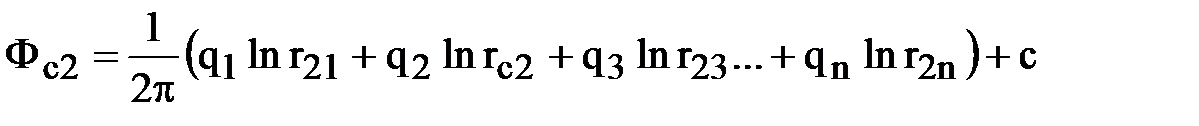 ,
,
………………………………………………………….
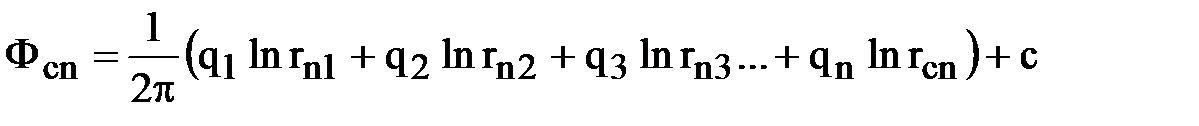 .
.
Система состоит из n уравнений и содержит n+1 неизвестных (n дебитов и постоянную интегрирования с). Дополнительное уравнение получим, поместив точку М на контур питания:
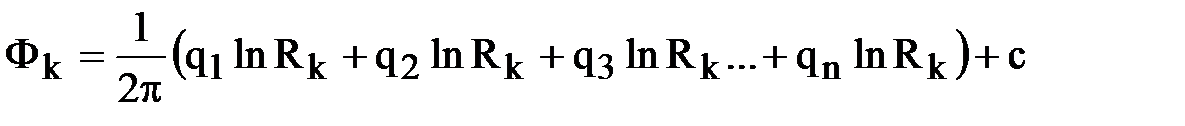 .
.
Вычитая почленно уравнения системы из последнего уравнения (исключая тем самым с), получим новую систему из n неизвестных относительно qi:
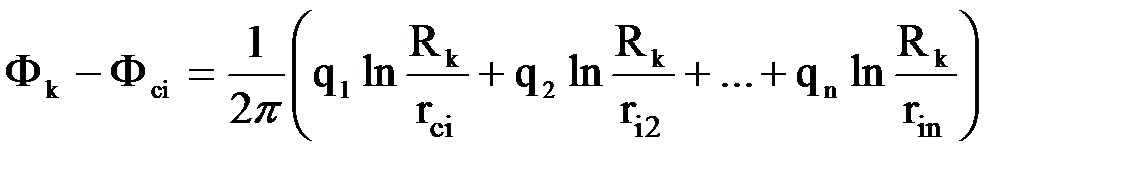 , i = 1, 2 ... n..
, i = 1, 2 ... n..
 На основании этих уравнений можно также определить неизвестные потенциалы по известным дебитам.
На основании этих уравнений можно также определить неизвестные потенциалы по известным дебитам.
 в любой точке пласта М определяется как геометрическая сумма скоростей фильтрации, вызванных работой каждой скважины (рис.15.5).
в любой точке пласта М определяется как геометрическая сумма скоростей фильтрации, вызванных работой каждой скважины (рис.15.5).
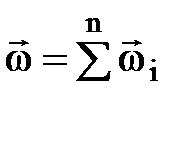 ;
;  .
.
Рис. 15.5
3.8.3. Приток жидкости к скважине с прямолинейным контуром питания.
Пусть в полубесконечном пласте на расстоянии a от прямолинейного контура питания с контурным потенциалом Фk, работает в точке А одна добывающая скважина забойным потенциалом Фс. Требуется найти удельный дебит (q), скорость фильтрации (  ) и потенциал (Ф) в любой точке пласта М (рис. 15. 6).
) и потенциал (Ф) в любой точке пласта М (рис. 15. 6).

| Рис. 15.6 |
Формула потенциала точечного стока 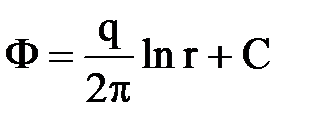 справедлива, если скважина расположена в бесконечном пласте или в центре пласта с круговым контуром питания, когда обеспечено плоскорадиальное течение.
справедлива, если скважина расположена в бесконечном пласте или в центре пласта с круговым контуром питания, когда обеспечено плоскорадиальное течение.
Условие постоянства контурного потенциала Фk здесь не выполняется из-за конечного расстояния до контура питания. Для решения задачи используем рассмотренный метод отображения стоков и источников.
Влияние прямолинейного контура приводит к появлению фиктивного зеркального источника –q* в точке А/ на расстоянии aот прямолинейного контура питания.
Потенциал в любой точке М пласта определяется как сумма потенциалов от двух источников:
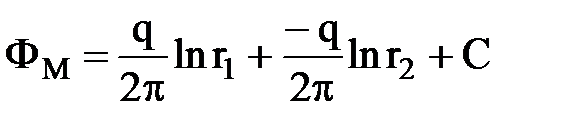 ,
,
где: q – действительный сток; -q – фиктивный источник.
Потенциал на контуре получим, полагая r1 = r2:
Фk = С = const.
Постоянство потенциала свидетельствует о корректности применяемого метода. Для вычисления дебита скважины найдем ее забойный потенциал, переместив точку М на забой скважины, т.е. положив r1 = rс и r2 = 2a:
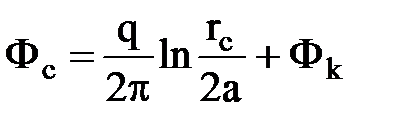 , отсюда
, отсюда 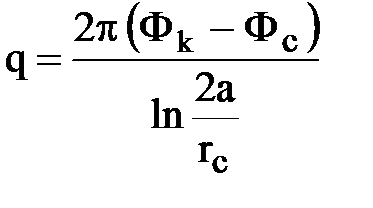 .
.
Формула совпала с формулой Дюпюи при условии Rк = 2а.
В реальных условиях форма контура питания неизвестна, но вероятней всего она располагается между окружностью радиуса а и прямой, которой соответствует Rк =2а (рис. 15.7).

|
| Рис. 15.7 |
Поэтому удельный дебит q определяется из неравенства:
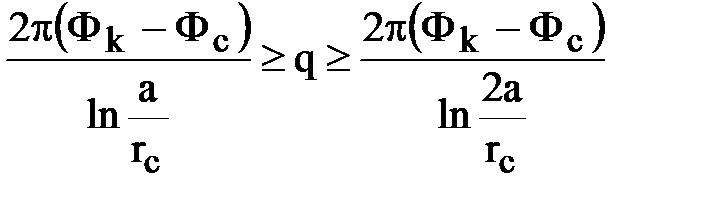 .
.
Найдем теперь гидродинамическое поле точечного источника возле прямолинейного контура как совокупность эквипотенциалей и линий тока.
Уравнение линии равного потенциала можно поучить из выражения потенциала в любой точке М (х, у) пласта  .
.
Положив этот потенциал постоянной величине и представив радиусы-векторы r1 и r2 в координатой форме, найдем уравнение линии равного потенциала, проходящей через точку М: 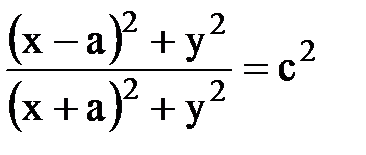 .
.
Это уравнение можно преобразовать к уравнению семейства окружностей с центрами, лежащими на оси x:
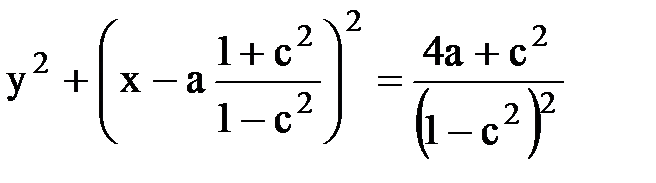 .
.
Аналогично можно показать, что семейство линий тока также будет представлять окружности, но с центрами на оси у. Окружности будут перпендикулярными к эквипотенциалям и проходить через сток и фиктивный источник (рис.15.8).

|
| Рис. 15.8. |
3.8.4. Приток жидкости к скважине, расположенной вблизи непроницаемой прямолинейной границы.

| Рис. 15.9. |
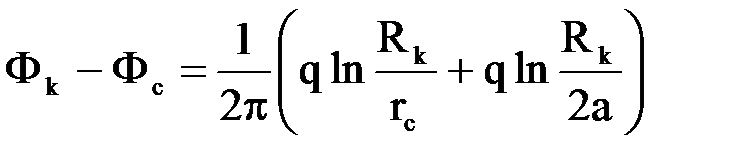 ,
,
где: 2а = r12, отсюда
 .
.
Лекция №16
3.8.5. Приток жидкости к скважине, эксцентрично расположенной в круговом пласте.
Пусть в плоском пласте мощностью h с круговым контуром питания радиуса Rк, на контуре которого поддерживается постоянный потенциал Фk, на расстоянии d от центра в т. A расположена скважина-сток, с забойным потенциалом Фс. Требуется определить дебит скважины и потенциал ФM (х, у) в любой точке пласта M (рис. 16.1).
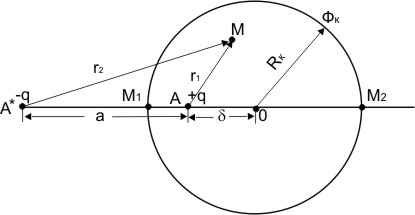 Рис. 16.1
Рис. 16.1
Воспользуемся методом отображения стока в круге радиусом Rk. В этом случае отображением стока +q в т. A будет источник –q в т. A*, расположенной на продолжении ОА на расстоянии «а» от т. А. Найдем это расстояние из условия постоянства Фk на круге, в частности в 2-х его точках М1 и М2:
 ;
;
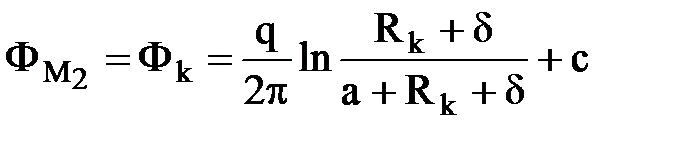 ;
;
 ;
;  .
.
Для того, чтобы определить дебит скважины в т. А запишем выражение ее забойного потенциала:
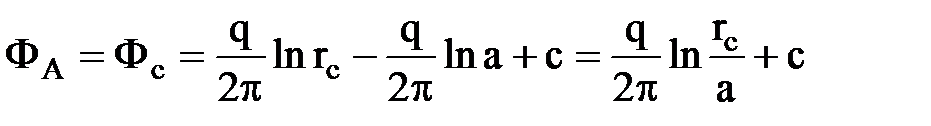 .
.
Чтобы избавиться от константы вычтем полученное выражение забойного потенциала из выражения контурного потенциала в т. M1:
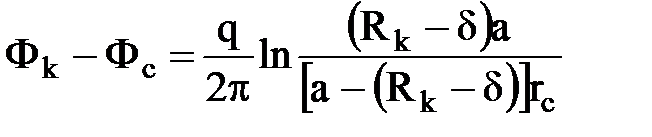 .
.
Подставляя сюда значение а, получим:
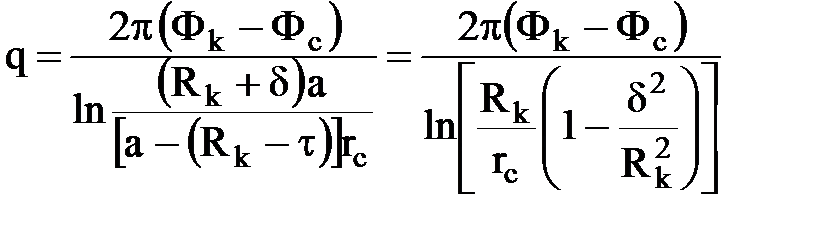 ,
,
при d = 0 формула переходит в формулу Дюпюи. Выражение потенциала в любой точке М:
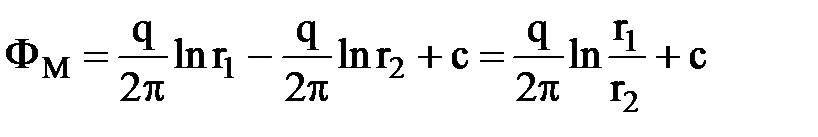 .
.
Вычитая из этого выражения уравнение ФМ1=Фk и учитывая выражение для «а», получим:
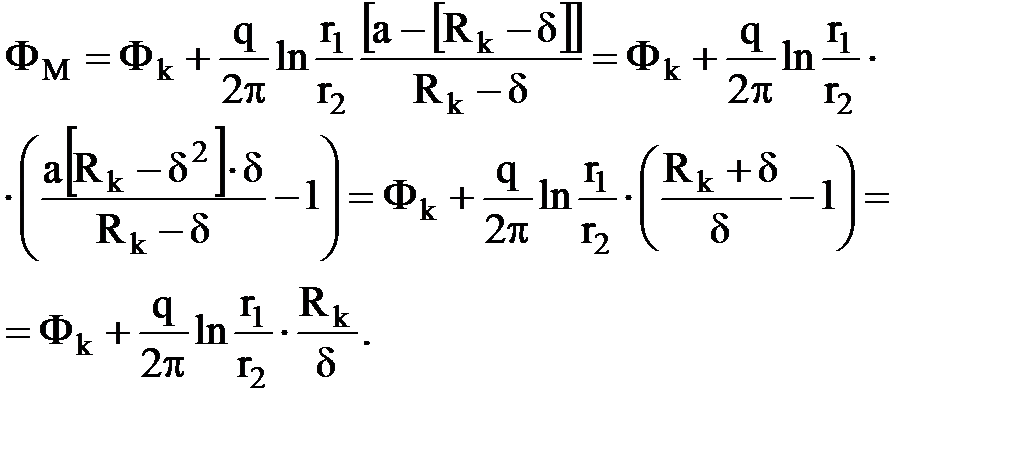
3.9. Метод электрогидравлических аналогий -метод эквивалентных фильтрационных сопротивлений.
На примере притока жидкости к нескольким рядам (плоскопараллельный поток) или кольцеобразным батареям скважин (плоскорадиальный поток) ознакомимся с широко применяемым на практике при проектировании разработки месторождений методом эквивалентных фильтрационных сопротивлений. Метод предложен Ю.А. Борисовым и основан на аналогии движения жидкости в пористой среде и электрического тока в проводниках.
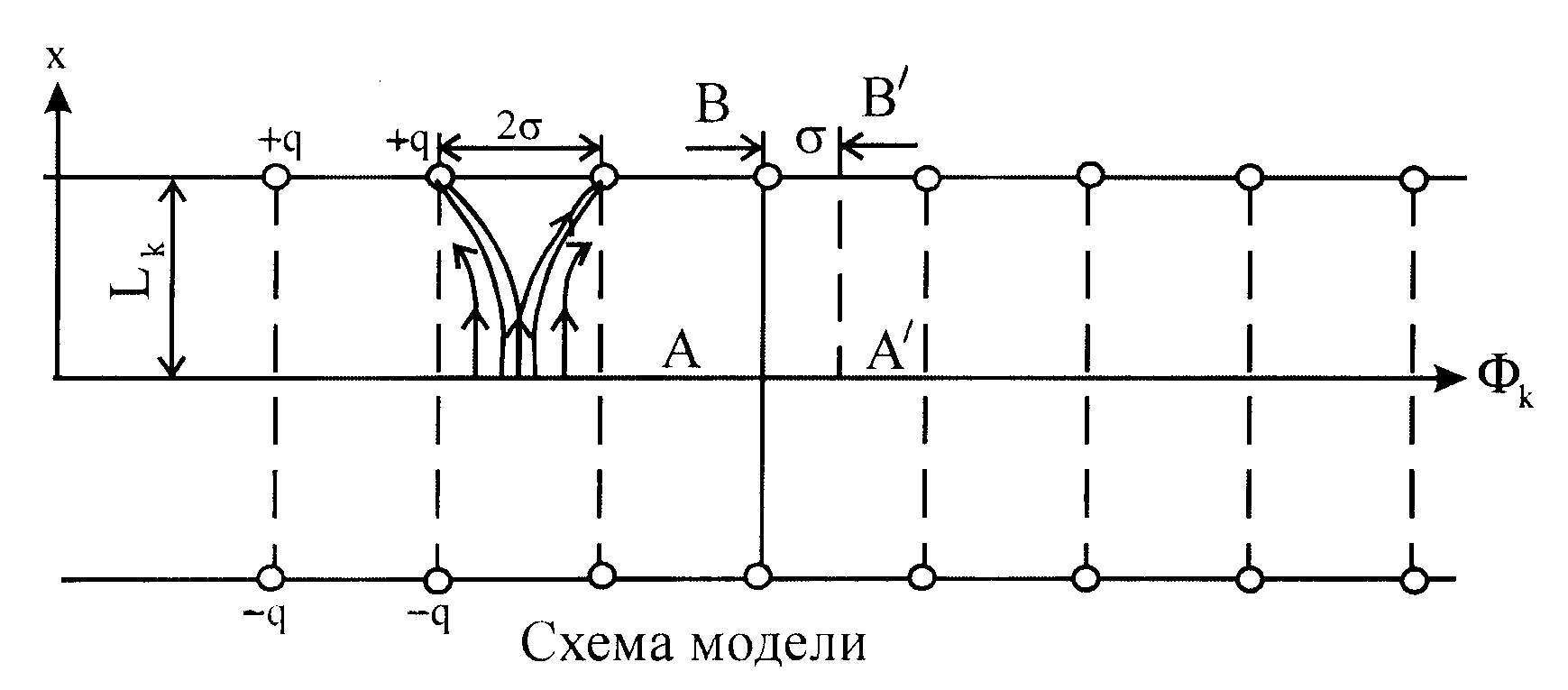
Рис. 16.2
| Задача решается методом зеркального отображения цепочек скважин относительно прямолинейного контура питания. Расчеты показывают, что до половины расстояния от контура до цепочки движение жидкости плоскопараллельное (здесь падение потенциала пропорциональное и незначительное), а вблизи скважин–плоскорадиальное (здесь основное падение потенциала) (рис. 16.2 и 16.3). |
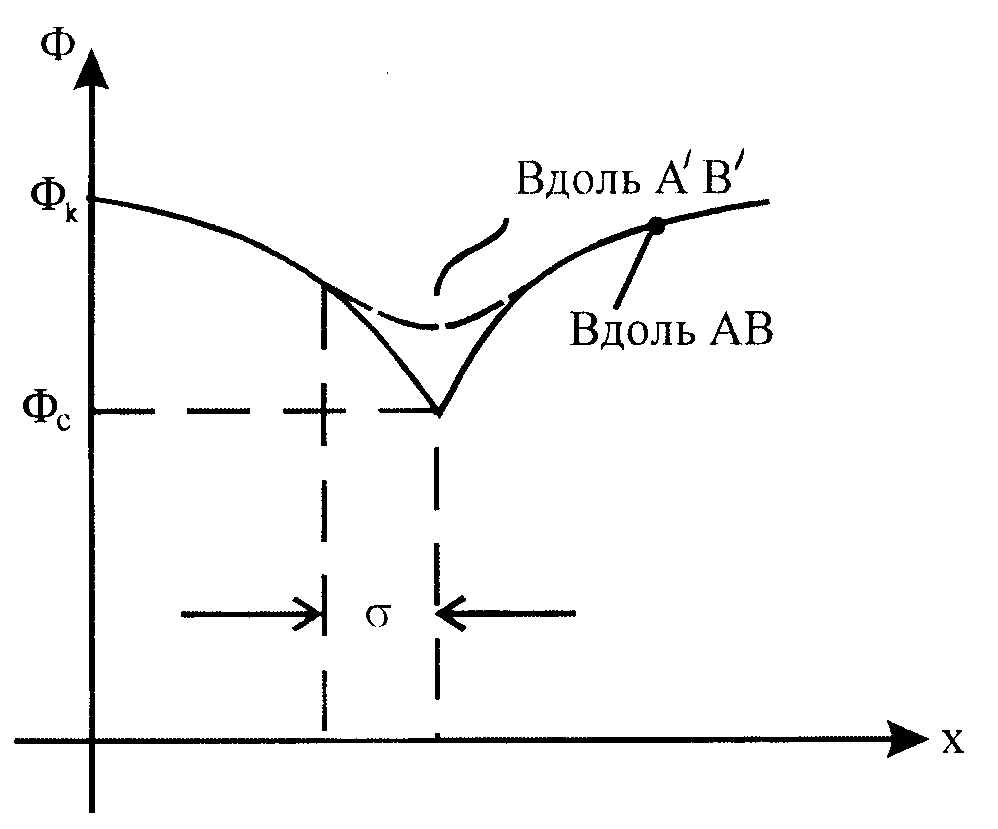 Модель (L, Фк, Фс) – цепочка скважин на расстоянии 2s друг от друга и на расстоянии L от прямолинейного контура питания (рис16.2).
Модель (L, Фк, Фс) – цепочка скважин на расстоянии 2s друг от друга и на расстоянии L от прямолинейного контура питания (рис16.2).
Рис. 16.3
При этом удельный дебит каждой скважины по методу отображения равен:
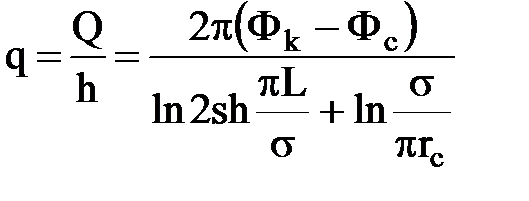 ,
, 
| Задача решается методом зеркального отображения цепочек скважин относительно прямолинейного контура питания. Расчеты показывают, что до половины расстояния от контура до цепочки движение жидкости плоскопараллельное (здесь падение потенциала пропорциональное и незначительное), а вблизи скважин–плоскорадиальное (здесь основное падение потенциала) (рис. 16.2 и 16.3). |
Рис. 16.3
Рис. 16.3
П
где: 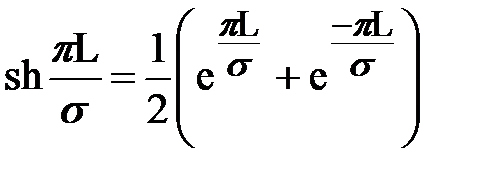 , при L >> s, величина
, при L >> s, величина 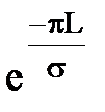 очевидно малая и
очевидно малая и 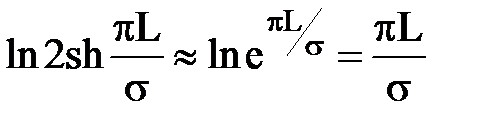 ,
,
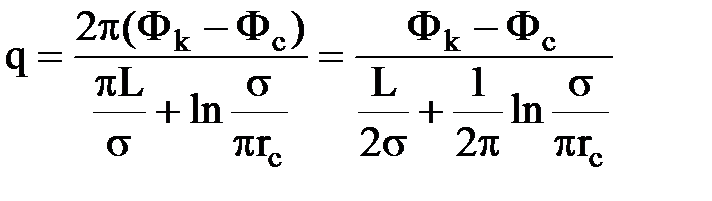 ,
,
где: 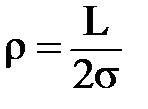 - внешнее фильтрационное сопротивление; а
- внешнее фильтрационное сопротивление; а 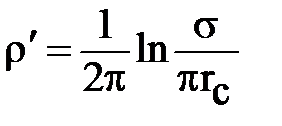 - внутреннее фильтрационное сопротивление.
- внутреннее фильтрационное сопротивление.
Введение фильтрационных сопротивлений r и r/ позволяет записать удельный дебит в форме аналогичной закону Ома: 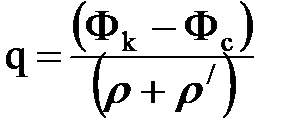 ,
,
где: q ® J; (Фk - Фc) ® Uk - Uc.
Суммарный дебит всей прямолинейной цепочки из n скважин:
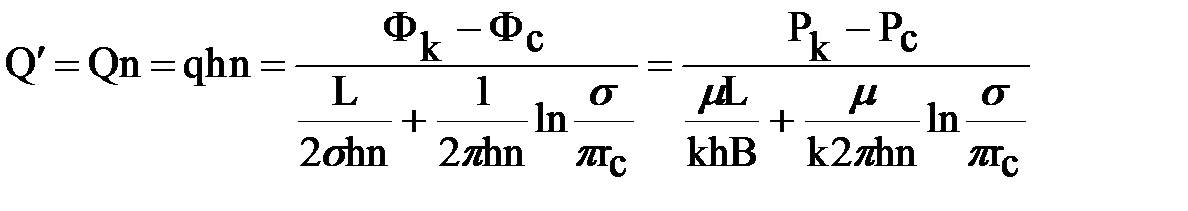 ,
,
где: 2sn = В – длина цепочки скважин.
Аналогично суммарный дебит круговой батареи из n скважин определяется выражением 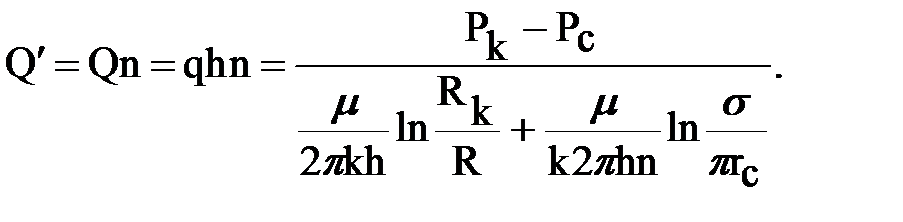 , где: Rk-радиус контура питания; R-радиус круговой батареи; s- половина расстояния между скважинами на контуре.
, где: Rk-радиус контура питания; R-радиус круговой батареи; s- половина расстояния между скважинами на контуре.
Введем аналогию между гидродинамическими характеристиками фильтрационного потока и характеристиками электрического тока: Q1/® I; (Pk-Pc)®DU; 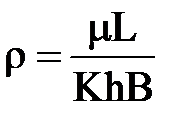 - внешнее фильтрационное сопротивление и
- внешнее фильтрационное сопротивление и 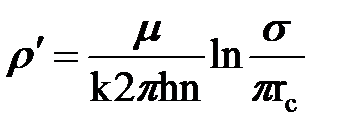 - внутреннее фильтрационное сопротивление.
- внутреннее фильтрационное сопротивление.
Тогда электрогидравлическая схема для одной цепочки (батареи) скважин будет иметь вид (рис. 16.4):
Сопротивление r представляет гидравлическое сопротивление потоку жидкости шириной В на пути L от контура питания до галереи, а r/ - отражает сопротивление потоку при подходе непосредственно к скважинам в зоне 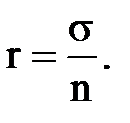
|

Рис. 16.4
Пусть теперь в полубесконечном пласте с прямолинейным контуром питания работают три параллельных цепочки добывающих скважин с числом n1, n2, n3 соответственно. Скважины в каждой цепочке имеют одинаковые радиусы 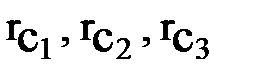 и забойные давления РС1, РС2, РС3, а суммарные дебиты цепочек равны, соответственно Q1/, Q2/, Q3/.
и забойные давления РС1, РС2, РС3, а суммарные дебиты цепочек равны, соответственно Q1/, Q2/, Q3/.
Электрогидравлическая схема будет состоять из трех цепочек фильтрационных сопротивлений и будет выглядеть (рис. 16.5):
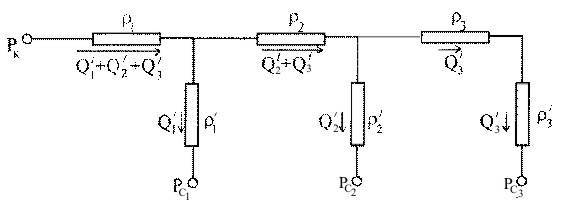
Рис. 16.5
Расчет схемы производится аналогично расчету разветвленных электрических цепей по законам Ома и Кирхгофа. Составляются алгебраические линейные уравнения по числу неизвестных: дебитов Q1/, Q2/, Q3/ (токов), если известны забойные давления (потенциалы), или наоборот.
Внешние сопротивления рассчитываются по формуле
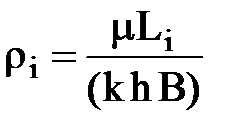 ,
,
где: 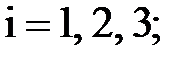 Li – расстояние от контура питания до i-й цепочки.
Li – расстояние от контура питания до i-й цепочки.
Внутренние сопротивления будут
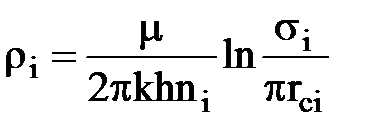 , i = 1, 2, 3….
, i = 1, 2, 3….
Отметим, что приток жидкости к трем кольцевым батареям скважин с круговым контуром питания рассчитывается по такой же схеме электрических сопротивлений; при этом сохраняются и формулы расчета внутренних фильтрационных сопротивлений, а внешние сопротивления рассчитываются по формуле
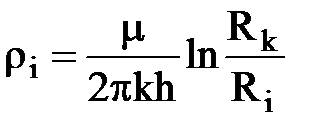 , i = 1, 2, 3…..
, i = 1, 2, 3…..
При расчете фильтрационных сопротивлений следует учитывать, что номера прямолинейных или кольцевых батарей отсчитываются от контура питания. Контур питания первой батареи совпадает с истинным контуром, а каждой последующей, совпадает с положением линии предыдущей батареи (рис. 16.6).
Расстояния Li для расчета внешних фильтрационных сопротивлений плоскорадиального потока показаны на рисунке 16.6-а, а для расчета ана-
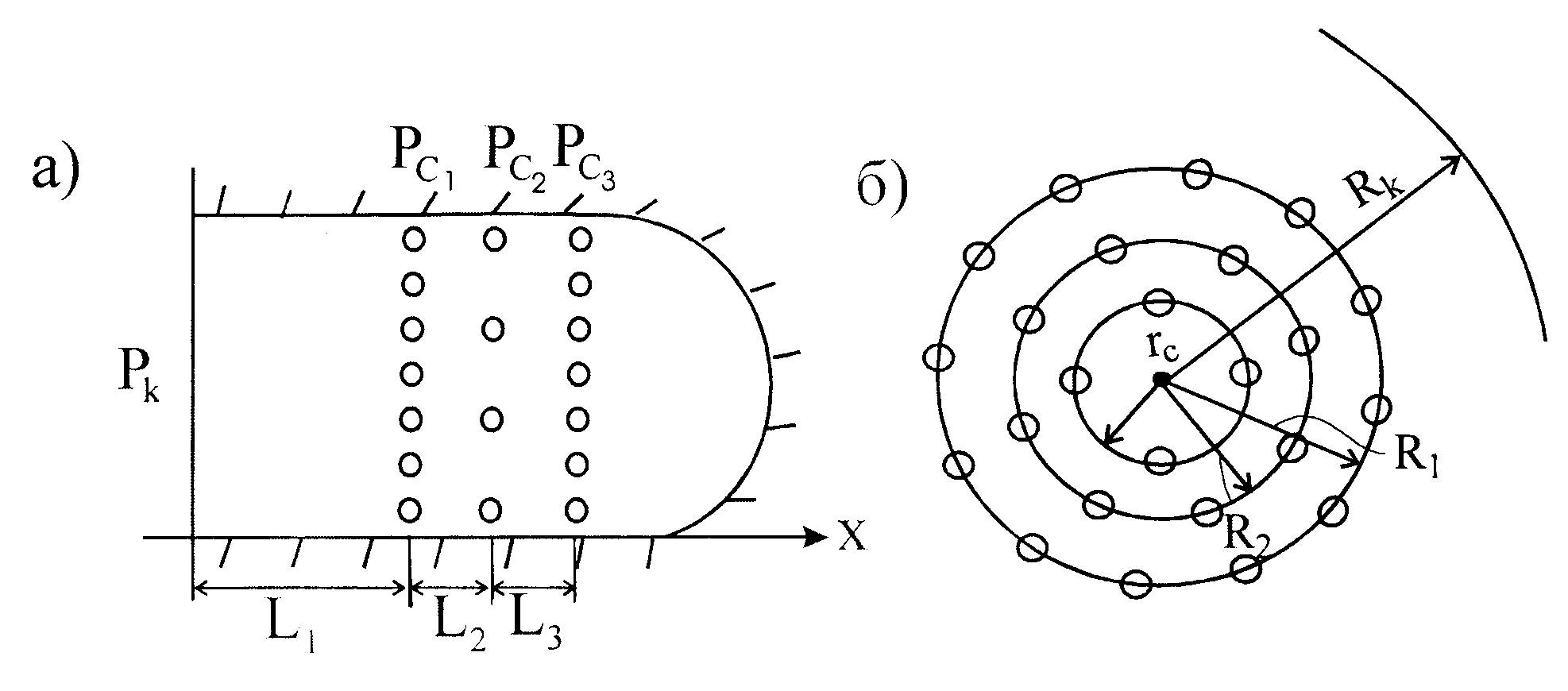
Рис. 16.6
логичных сопротивлений круговых батарей соотношение 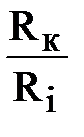 будет следующим: для первой батареи
будет следующим: для первой батареи 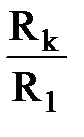 , для второй
, для второй 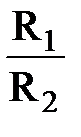 , для третьей
, для третьей 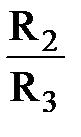 и т.д.
и т.д.
3.10. Приток жидкости к несовершенным скважинам.
Лекция № 17
Скважина называется гидродинамически совершенной, если она вскрывает пласт на всю его мощность и на этом интервале скважина не обсажена (открыта), так что вскрытая поверхность забоя является фильтрующей.
Скважина называется несовершенной по следующим условиям:
- по степени вскрытия пласта (пласт вскрыт не на всю мощность), при этом ђ = b/h – называется относительным вскрытием пласта, где b – вскрытая мощность;
- по характеру вскрытия; скважина обсажена (или в ней находится специальный фильтр) и она сообщается с пластом через перфорационные отверстия в трубе (цементе) или отверстия в фильтре.
Встречаются скважины с двойным несовершенством. Гидродинамическое несовершенство скважин оценивается коэффициентом d = Q/Qсов.
Приток жидкости к несовершенной скважине даже в бесконечном горизонтально - однородном пласте перестает быть плоскорадиальным. Строгие математические решения задач притока жидкости к несовершенным скважинам представляют большие трудности. Существует несколько подходов к решению таких задач:
1. Расчетный. Задача о притоке жидкости к несовершенным скважинам по степени вскрытия пласта математически исследовалась М. Маскетом. При этом получена следующая формула для дебита:
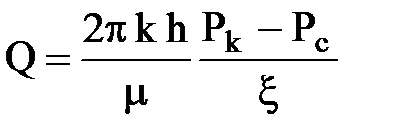 ,
,
где: 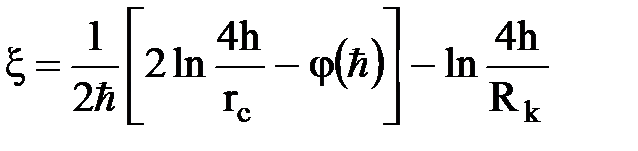 ,
, 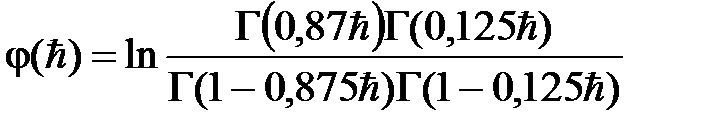 .
.
j 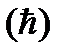
|
| ô ô ô ô ô 0 0,2 0,4 0,6 0,8 1,0 |
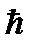
|
 - интеграл 2-го ряда Эйлера (Гамма-функция, для которой имеются таблицы в математическом справочнике). График j (ђ) имеет вид (рис 17.1).
- интеграл 2-го ряда Эйлера (Гамма-функция, для которой имеются таблицы в математическом справочнике). График j (ђ) имеет вид (рис 17.1).
| Нетрудно видеть, что при ђ = 1 формула Маскета переходит в формулу Дюпюи для плоско-радиального потока. |
Рис. 17.1
Иногда для расчета дебитов несовершенных по вскрытию пласта скважин используют формулу И. Козени:
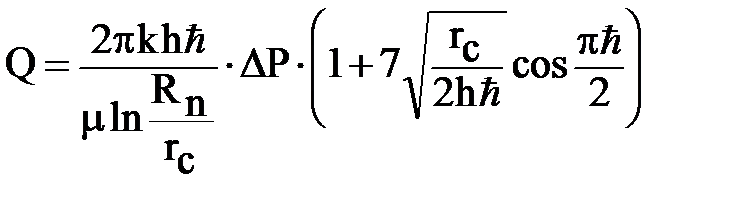 ; при ђ = 1 формула переходит в формулу Дюпюи.
; при ђ = 1 формула переходит в формулу Дюпюи.
Формула Козени удобна тем, что для рассчета не требует справочных данных Гамма-функции.
2. Электрическое моделирование, основанное на электрогидродинамической аналогии фильтрационных процессов.
Ванна заполняется электролитом. В электролит помещается кольцевой электрод, имитирующий контур питания, а в центре его погружается штыревой электрод-скважина на глубину, соответствующую степени вскрытия пласта скважиной. К обоим электродам подается разность потенциалов тока. Возникающий ток является аналогом дебита скважины.
Дебит гидравлически несовершенной скважины подсчитывается по формуле:
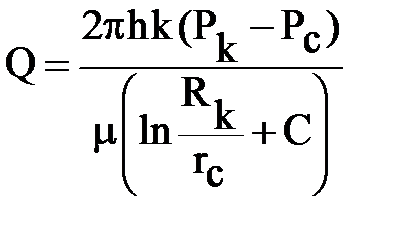 ,
,
где: C = с1+с2 – дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по степени вскрытия (с1) и характеру вскрытия (с2).
Измеряя разность потенциалов и силу тока, можно подсчитать по закону Ома общее сопротивление, сделать пересчет и определить дополнительные фильтрационные сопротивления.
Такие экспериментальные исследования проведены В.И. Щуровым. Им определены:
с1 = с1(а = h Dc, ħ = b/h) и с2 = с2 (n Dc, l = l/ /Dc, α = d/ /Dc),
где: n – число перфорационных отверстий на метр; Dc – диаметр скважины; l/ - глубина проникновения перфорационных пуль в породу; d/ - диаметр отверстий.
Составлены номограммы Щурова для определения с1 и с2 , первая из них показана на рис. 17.2.

|
| Рис. 17.2 |
.
3. И.А. Чарный предложил оценочный метод определения дебита, если величина b вскрытия пласта мала (b << h).
Область движения условно разбивается на две зоны: 1-я зона, где преимущественно плоскопараллельное движение от контура питания до зоны радиуса R0; 2-я зона, где движение можно считать сферически- радиальным от скважины до расстояния R0 (рис. 17.3).
| Rk |
| R0 |
| R0 |
| h |
| h |
| b |
| 2 rc |
| Рис. 17.3. |
Тогда дебит в первой зоне на ее границе со 2-й можно записать через формулу Дюпюи
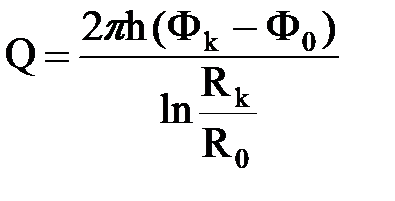 .
.
Дебит во второй зоне на ее границе с первой, учитывая сферически-радиальный характер фильтрации, можно определить по формуле:
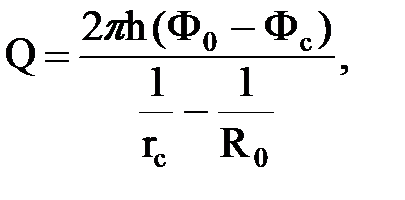
Приравнивая эти дебиты, в виду неразрывности потока, и применяя правило преобразования пропорции, получаем формулу обобщенного дебита для скважины, вскрывшей пласт на малую глубину:
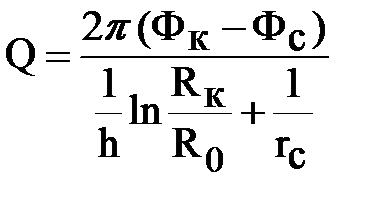 ,
,
принимая R0 = 1,5 h, получаем окончательную формулу:
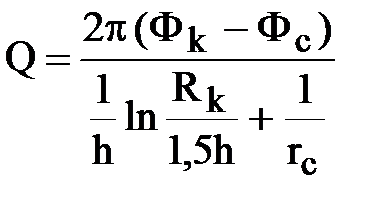 .
.
Задачи притока жидкости к скважинам, несовершенным по характеру вскрытия и с двойным несовершенством, еще сложнее.
На практике удобно рассчитывать дебит гидравлически несовершенной скважины также по формуле Дюпюи, но в этом случае в ней фигурирует не истинный радиус скважины, а приведенный:
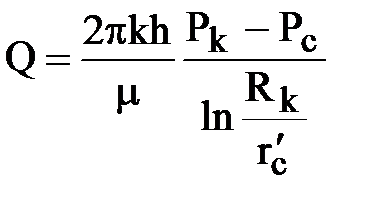 ,
,
где: 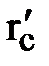 - приведенный радиус. Найдем его, приравняв дебиты скважины, выраженные через приведенный радиус и через фильтрационные сопротивления:
- приведенный радиус. Найдем его, приравняв дебиты скважины, выраженные через приведенный радиус и через фильтрационные сопротивления:
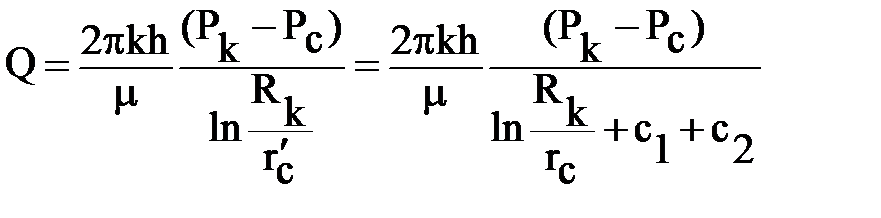 .
.
Приравнивая, получим:  ,
, 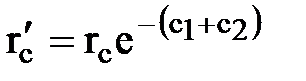 .
.
Этот прием позволяет рассчитать дебит несовершенных скважин по известной формуле Дюпюи, но с приведенным радиусом.
Иногда гидродинамическое несовершенство учитывается при помощи коэффициента несовершенства d, вычислив который как отношение дебита несовершенной скважины к дебиту совершенной, можно определить коэффициент C=с1 +с2 , выражающий сумму дополнительных фильтрационных сопротивлений
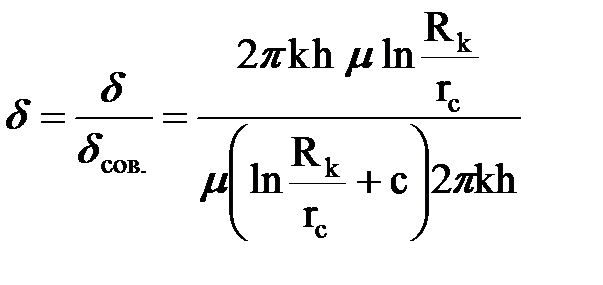 ;
;
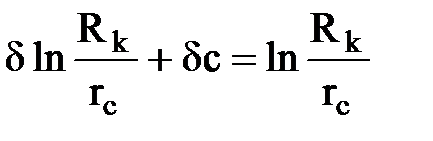 ;
;
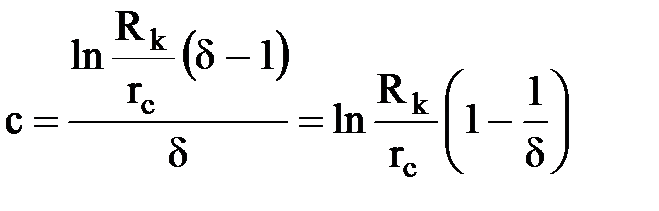 .
.
Дата добавления: 2017-02-20; просмотров: 2323;
