Одномерные фильтрационные потоки несжимаемой жидкости при нелинейных законах фильтрации
Лекция № 13
Обобщим результаты для случая фильтрации несжимаемой жидкости при больших скоростях движения, когда становятся значительными инерционные силыстемы и основу уравнения движения должен составить не закон Дарси, а степенные функции:
| сила вязкого трения |
| потеря давления |
| инерционная сила |
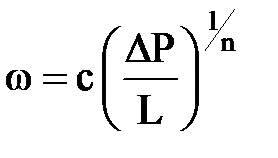 и
и  .
.
Для таких простейших случаев одномерных потоков несжимаемой жидкости решения (P, w, Q) можно получить, не прибегая к уравнению Лапласа, а используя только уравнение движения и его связь с дебитом. Это становится возможным потому, что дебит в таких случаях постоянный, либо является простой функцией координаты движения, что позволяет разделить переменные
1. Прямолинейно-параллельный установившийся фильтрационный поток.
Схема фильтрации та же, но вместо закона Дарси используется нелинейный степенной закон фильтрации (рис. 13.1 и рис. 13.2).
Pk Pr
 °
x °
°
°
°
Lk °
x °
°
°
°
Lk
|
|
. . . . . .
. . . . . .
. . . . . .x
. . . . . .
| Рис. 13.1 |
| Рис. 13.2 |
Схема фильтрации та же, но вместо закона Дарси используется нелинейный степенной закон фильтрации (рис. 13.1 и рис. 13.2).
Для таких простейших случаев одномерных потоков несжимаемой жидкости решения (P, w, Q) можно получить, не прибегая к уравнению Лапласа, а используя только уравнение движения и его связь с дебитом. Это становится возможным потому, что дебит в таких случаях постоянный, либо является простой функцией координаты движения, что позволяет разделить переменные. Составим уравнение, левая часть которого выражает скорость фильтрации через нелинейный закон движения, а правая – скорость, выраженную через объемный дебит и площадь фильтрации
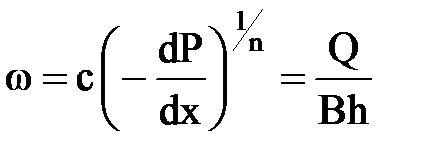 ; 1 < n < 2.
; 1 < n < 2.
Разделяя переменные и интегрируя в соответствующих пределах, найдем Q:
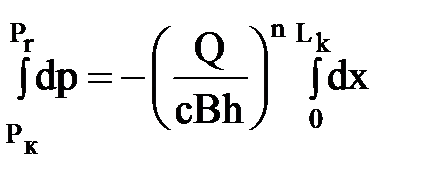 ; откуда
; откуда 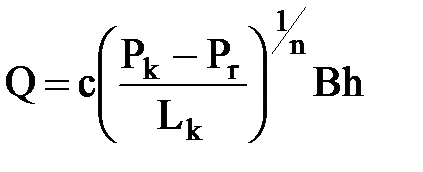 ,
,
интегрируя в переменных пределах, найдем распределение давления.
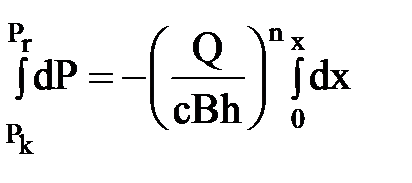 ;
; 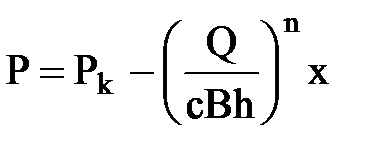
или подставляя сюда выражение Q, получим:
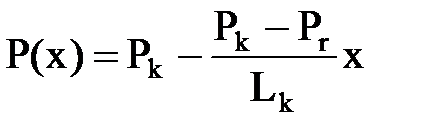 ,
,
что в точности совпадает спри фильтрациейи по линейному закону Дарси.
Находим градиент давления
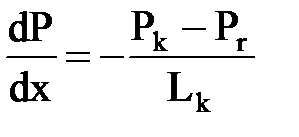
и скорость фильтрации
 ,
,
будет постоянной и не зависит от координаты движения.
2. Плоскорадиальный фильтрационный поток несжимаемой жидкости.
Моделью является круговой пласт постоянной мощности, в центре пласта расположена добывающая скважина. Движение жидкости к скважине -по координате r. Начало координат на скважине. Составим уравнение, левая часть которого, как и раньше, выражает скорость фильтрации при нелинейном законе движения, а правая – скорость, выраженную через объемный дебит и площадь фильтрации.
 ,
,
где 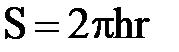 - площадь сечения пласта.
- площадь сечения пласта.
Разделяя здесь переменные и интегрируя, получим:
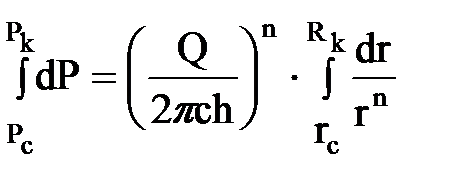 ;
;

Откуда
 .
.
В предельном случае при n = 2 (закон Краснопольского)
| если пренебречь |
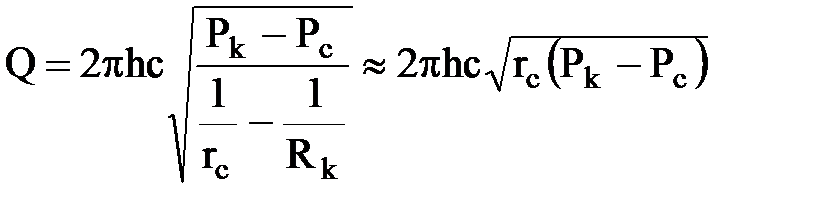 .
.
Распределение давления в потоке определим из предыдущего интегрируемого уравнения, проведя интегрирование его в переменных пределах, а затем подставив найденное выражение потока Q:
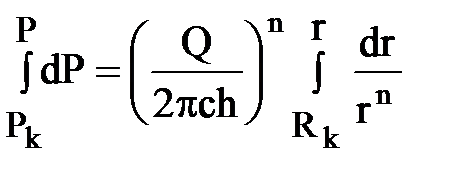 ;
; 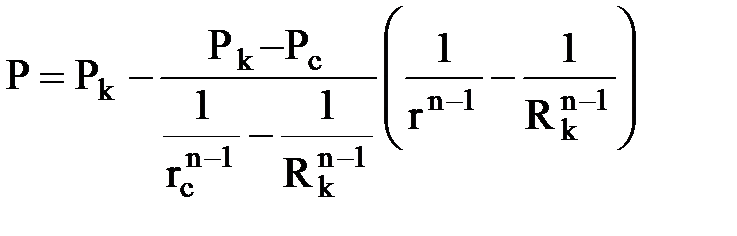 .
.
В случае закона Краснопольского (n = 2)
 ,
,
что совпадает с распределениемс решением давления при радиально-сферическом притотоке по линейному закону Дарси. Совпадает и градиент давления
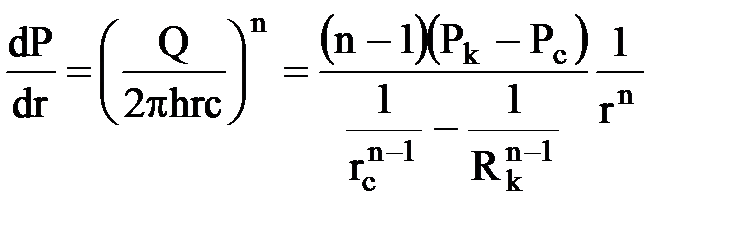 ;
;
при (n = 2) 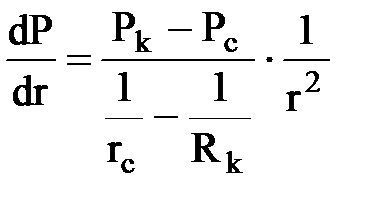 .
.
Скорость фильтрации w определяется
 .
.
К такому же результату приводит расчет по формуле 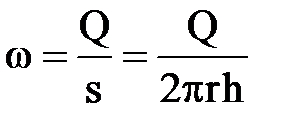 .
.
Индикаторные кривые, т.е. кривые дебита в зависимости от депрессии давления DР, имеют вид (рис. 13.3):
| n = 2 (параб.) |
| n = 1 |
| 1< n < 2 |
| DР = Рk - Рc |
| Q |
| Рис. 13.3 |
Кривая распределения давления в плоскорадиальном потоке при нелинейном законе фильтрации имеет форму гиперболы, а следовательно, воронка депрессии будет гиперболоидом вращения и будет круче, чем логарифмическая воронка в соответствующем потоке при линейной фильтрации (рис. 13.4).
| Рис. 13.4. |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| закон Дарси |
| нелиней. закон |
| Рс |
Следует отметить, что в реальных условиях нельзя считать, что во всем
пласте – от стенки до контура питания справедлив один нелинейный закон фильтрации с постоянным показателем степени n. Фильтрация может происходить по линейному закону при небольших дебитах, но с его ростом начнется нарушение линейности начнется, прежде всего, у забоя скважины, в то время как в остальной части пласта может сохраняться закон Дарси. В дальнейшем по мере увеличения дебита область потока, в которой нарушен закон Дарси, будет расширяться.
В этих случаях необходимо использовать двухчленный закон функции
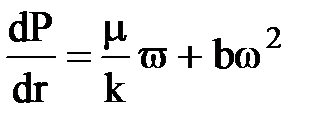 , где
, где  .
.
Выражая скорость фильтрации через дебит  , перепишем двухчленный закон
, перепишем двухчленный закон
 ,
,
разделяя здесь переменные, получим
 .
.
Проинтегрировав здесь соответственно от r до Rk и от Р до Рк, найдем:
а) распределение давления в пласте
 ;
;
б) дебит скважины, как положительную переменную квадратного уравнения
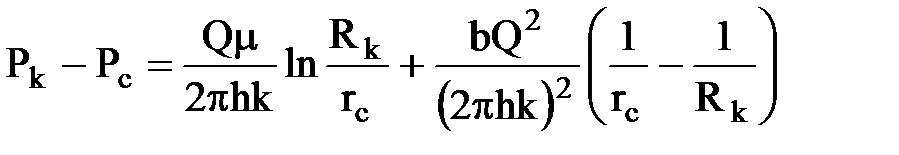 .
.
Дата добавления: 2017-02-20; просмотров: 1293;
