Дифференциальные уравнения фильтрации флюидов

Лекция № 8

1. Закон Дарси, связывающий давление флюида и скорость фильтрации получен экспериментальным путем на лабораторной установке с известными геометрическими размерами (L, S) и постоянными характеристиками пористой среды, для однородного течения жидкости при постоянном расходе флюида.

В реальных условиях исчезает понятие о геометрических размерах пористой среды (ввиду масштабности), ее характеристики изменяются от точки к точке и во времени, т.е. мы имеем дело с полем давлений и скоростей. Характеристики этого поля получают на основании решения дифференциального уравнения в частных производных, используя при этом так называемые начальные и граничные условия.

Чтобы вывести дифференциальное уравнение фильтрации в пористой среде, заключающей движущийся флюид, вначале составляется система уравнений, в которой на основе соответствующих физических законов рассматриваются в бесконечно малом элементарном объеме изменение его массы и энергии, а также результаты экспериментального изучения поведения флюидов и свойств пористой среды. Число уравнений в системе (дифференциальных и конечно-разностных) должно равняться числу неизвестных функций, характеризующих процесс и подлежащих определению. Такая система уравнений называется замкнутой.

В число дифференциальных уравнений обязательно входят: уравнение баланса массы, уравнение неразрывности, уравнение движения и уравнения состояния параметров пористой среды и насыщающих ее флюидов.

В результате интегрирования (решения) дифференциальных уравнений получают, прежде всего, распределение давления и скорости фильтрации по всему пласту в любой момент времени.

Р = P(x, y, z, t); .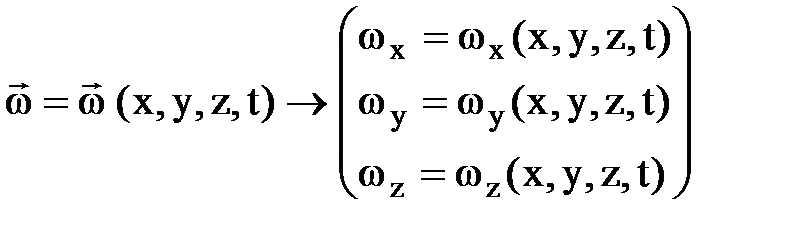

Для случая несжимаемого флюида (r=const) и постоянных параметров пористой среды (k, m=const) – это и будет решением. А в случае сжимаемых сред и флюидов нужно дополнительно определять r, m, m и k как функции координат пространства и времени.

Аналитическое (в виде формул) решение системы дифференциальных уравнений удается получать в ограниченном числе простейших случаев. В более сложных случаях системы уравнений решаются численными методами на ЭВМ. Вместе с тем знание аналитических решений для простых случаев (гидродинамических моделей) имеет большое значение, как для понимания законов гидродинамики так и потому, что сложные модели при определенных условиях сводятся к простым.

2. Вывод уравнения неразрывности.

Для однородного сжимаемого флюида и деформируемой среды уравнение неразрывности получается из уравнения баланса массы в элементарном объеме пористой среды.

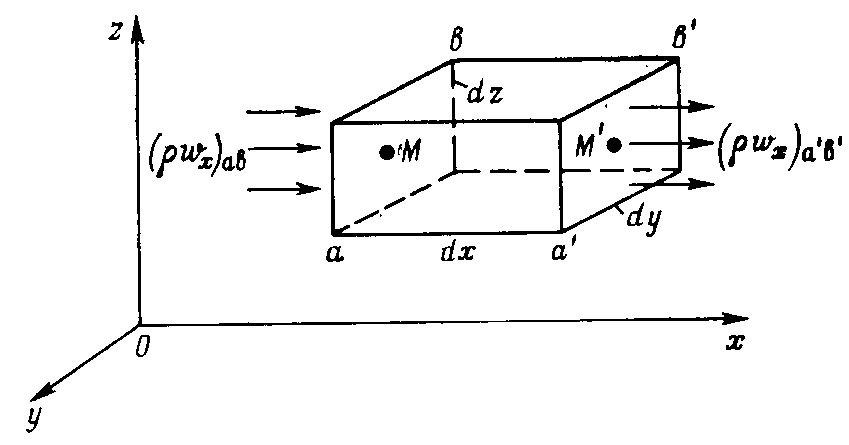
Рис. 8.1

Найдем поток жидкости (массовый) через левую грань за время t (точка М в центре грани).

N₁=(rw_x)_abdydzdt.