Уравнения состояния флюидов и параметров пористой среды
(Зависимость параметров флюида и пористой среды от давления)
Лекция № 9
Лекция № 9
Выведенные ранее дифференциальные уравнения содержат параметры флюида (r, m) и пористой среды (k, m). Для дальнейших расчетов необходимо знание зависимости этих параметров от давления.
Определение зависимости r = r (P) для жидкости
При установившейся фильтрации, например, считается r - const, однако при неустановившейся фильтрации (например, отборе флюида за счет расширения жидкости при снижении давления в скважине), необходимо учитывать сжимаемость жидкости.
Считая жидкость упругой, можно записать:
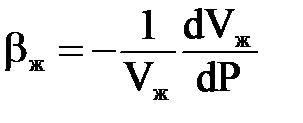 ,
,
где: bж – коэффициент объемного сжатия жидкости; 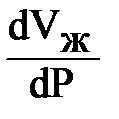 - изменение объема жидкости; Vж – первоначальный объем.
- изменение объема жидкости; Vж – первоначальный объем.
Эта формула устанавливает коэффициент сжимаемости как относительное изменение объема жидкости при изменении давления. Иногда используют модуль упругости
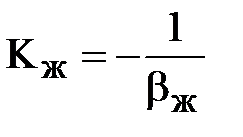 .
.
Для различных нефтей отечественных месторождений bн= (7¸30)×10-10Па-1, пластовой воды bв= (2,5¸5)×10-10Па-1.
Чтобы найти зависимость r = r(P) подставим в уравнение сжимаемости
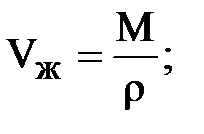
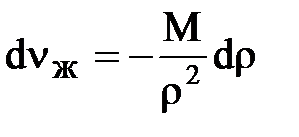 ;
;
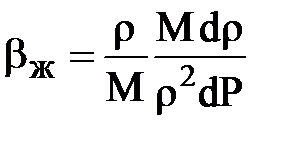 или
или 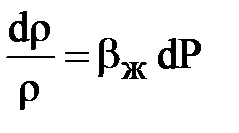 ;
;
интегрируя это уравнение 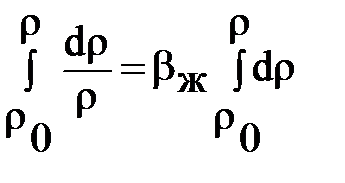 , получим
, получим
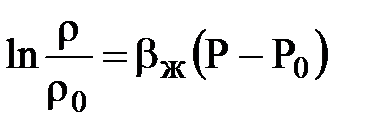 ;
; 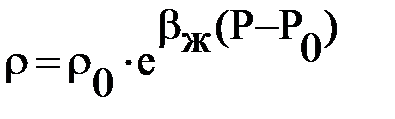 .
.
Показатель степени экспоненты для рядовых давлений Р£10Мпа=107Па и bж=10-10Па-1 обычно мал и составляет ~ 0,01. Поэтому, раскладывая экспоненту в ряд Тейлора в окрестности Р0 и ограничиваясь двумя членами, получим линейную зависимость:
r = r0 [1+bж (P-P0)].
Определение зависимости r = r (P) для газа.
Подземные природные газы можно считать идеальными и подчиняющимися уравнению Клапейрона-Менделеева, если пластовое давление невелико (6-9 МПа) и газ отбирается с депрессией до 1 МПа.
Тогда, если температура пласта постоянная (изотермический процесс) можно записать  (плотность газа пропорциональна давлению, что вытекает из уравнения Клапейрона).
(плотность газа пропорциональна давлению, что вытекает из уравнения Клапейрона).
Для месторождений с высоким пластовыми давлениями (до 40-60 МПа) и большими депрессиями отбора (15-30 МПа) для получения зависимости плотности газа от давления нужно использовать уравнение состояния реального газа
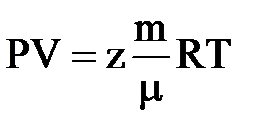 или
или 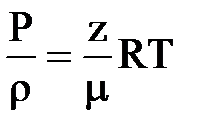 ,
,
где: m – масса газа, m - молекулярный вес, z = z (Pr, Tr) - сверхсжимаемость газа, определяется (как рассмотрено ранее) по графикам Д. Брауна в зависимости от приведенных величин давления (Рr) и температуры (Тr)

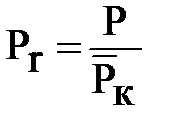 ;
; 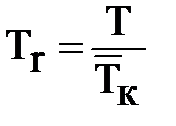 ,
,
где: 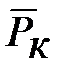 и
и 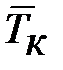 – псевдокритические значения давления и температурой для смеси природного газа. Определение их дано ранее.
– псевдокритические значения давления и температурой для смеси природного газа. Определение их дано ранее.
Используя найденное значение z (Pr, Tr) для изотермической фильтрации реального газа получим:
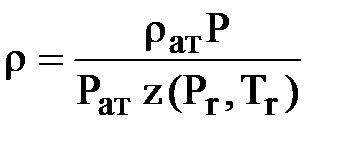 .
.
Определение зависимости m = m (Р)
Эксперименты показывают, что вязкость нефти при давлении выше давления насыщения и значительном изменении давления (до 100 МПа) увеличивается с повышением давления по зависимости
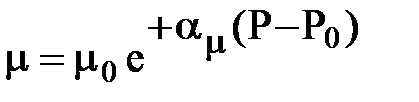
при незначительных изменениях давления
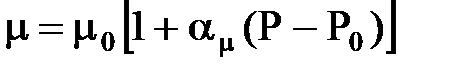 ,
,
где: m0 - вязкость при фиксированном давлении Р0; am - коэффициент, определяемый экспериментально и зависящий от химического состава нефти.
Определение зависимости k = k (P).
Зависимости проницаемости пласта k от давления описывается уравнениями, аналогичными зависимостям плотности и вязкости флюидов от давления.
k = k0[1+ak(P-P0)] – при малых изменениях P;
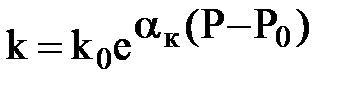 – при значительных изменениях Р.
– при значительных изменениях Р.
Учет изменения k = k (P) необходим чаще в трещинных коллекторах, чем гранулярных, т.к. изменения проницаемости в них более значительные.
Определение зависимости m = m(P).
Чтобы выяснить, как зависит пористость от давления, рассмотрим вопрос о напряжениях в пористой среде, заполненной жидкостью
Ргрн = (1–m)×s+mP,
где: Ргрн= rgH – горное давление на пласт; r - средняя плотность в покрывающей толще пород; Н –глубина залегания пласта; m – пористость; P – пластовое давление.
Тогда 1-е слагаемое в правой части является напряжением в скелете, а 2-е давлением поровой жидкости. Уравнение выражает следующее физическое содержание. Горное давление уравновешивается напряжением в скелете и давлением поровой жидкости (если кровля и почва пласта непроницаемые и пласт берет на себя нагрузку вышележащих пород).
Вводят так называемое эффективное напряжение, определяемое как разность напряжений в твердом скелете и жидкой фазе и действующее на скелете
sэф = (1-m)(s-P).
Тогда баланс напряжений можно записать:
Ргрн = sэф+Р = соnst.
Эффективное напряжение физически интерпретируется как часть истинного напряжения, которое передается по контакту между зернами.
При разработке месторождения (отбора нефти) sэф в скелете растет, т.к. снижается пластовое давление в жидкой фазе.
Пористость в общем случае зависит от sэф и Р,
m = m (sэф, P).
Снижение пластового давления жидкости
| m1 |
| m2< m1 |
| Ргрн |
| Pгрн |
| б) |
| а) |
| Рис. 9.1 |
В тех случаях, когда горное давление Ргрн=const, обычно считают пористость зависящей только от пластового давления и эта зависимость линейная
m = m0[1+bm(P-P0)], где bm – коэффициент.
Лабораторные исследования дают оценку его значений bm=(0,32¸2)×10-10Па-1.
При значительных изменениях давления изменение пористости описываются уравнением
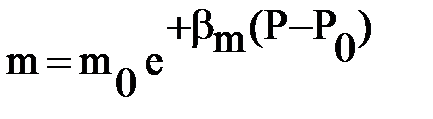
Таким образом, в общем случае нужно решить систему из 8-ми дифференциальных уравнений, включающую: уравнение неразрывности, три уравнения движения (одно в векторной форме, но три в скалярной), два уравнения состояния флюидов и два уравнения состояния пористой среды и определить функции от координат и времени: wx, wy, wz, P, r, m, m и k..
Начальные и граничные условия.
Продуктивный пласт или его часть можно рассматривать как некоторую область, ограниченную граничными поверхностями. Таких поверхностей много: кровля и подошва пласта, поверхности нарушений, выклинивания пласта, поверхности области питания (контура питания), стенки скважин и др.
Чтобы получить решения системы дифференциальных уравнений, к ней необходимо добавить начальные и граничные (краевые) условия.
Начальные условия заключаются в задании искомой функции во всей области в некоторый начальный момент времени.
Например: р = р(x, y, z) при t = 0; или P = const при t = 0, также и другие функции.
Граничные условия задаются на границах пласта. Возможны следующие граничные условия:
I. На внешней границе Г:
1) постоянное давление P = (Г, t) = Рк = const, т.е. граница является контуром питания;
2) постоянный приток через границу ¶P/¶n = const;
3) переменный приток через границу ¶P/¶n = f1(t);
4) замкнутая внешняя граница ¶P/¶n = 0;
5) бесконечный по простиранию пласт
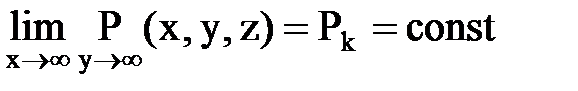 .
.
II. На внутренней границе:
6) постоянное давления на забое скважины радиусом rc
P(rc,t) = Pc = const;
7) постоянный дебит. Это условие при выполнении закон Дарси
можно представить следующим образом:
 =const или
=const или 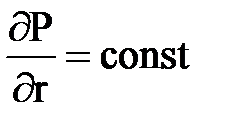 , при r = rc,
, при r = rc,
где: 2  rh - площадь боковой поверхности скважины;
rh - площадь боковой поверхности скважины;
8) переменный дебит 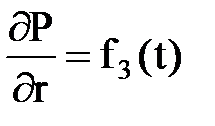 при r = rc;
при r = rc;
9) отключение скважины  при r = rc;
при r = rc;
Наиболее часто встречаются граничные условия 1 и 5, 6 и 7.
Лекция №10
3.4.Вывод дифференциального уравнения установившейся фильтрации несжимаемой жидкости по закону Дарси
В простейших идеализированных случаях рассмотренная ранее система дифференциальных уравнений первого порядка может быть представлена одним уравнением в частных производных более высокого порядка.
Выведем дифференциальное уравнение установившейся фильтрации несжимаемой жидкости по закону Дарси на основе уравнений неразрывности, движения и состояний жидкости и пористой среды (одно дифференциальное уравнение вместо системы дифференциальных уравнений).
Для таких условий без учета деформации среды (r, m = const) второй член уравнения неразрывности равен нулю и оно принимает вид:
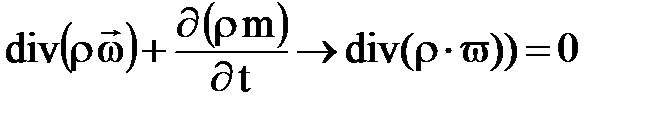 , и поскольку r ¹0, то
, и поскольку r ¹0, то
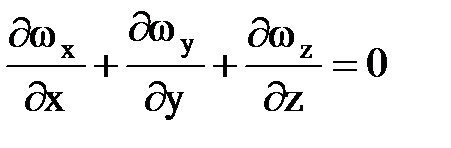 .
.
Уравнение движения по закону Дарси
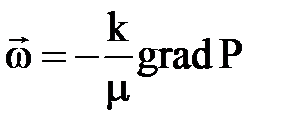 ,
, 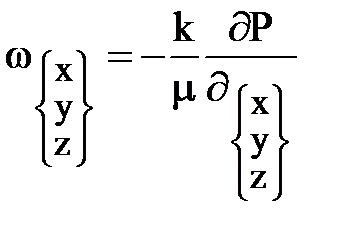 .
.
Определяем производные
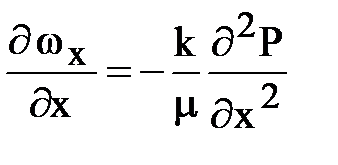 ;
;
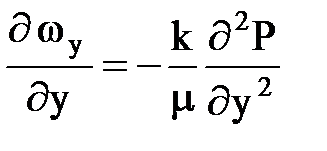 ;
;
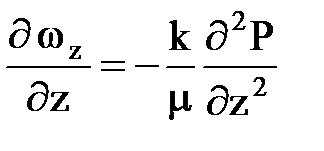 .
.
и подставляя выражение w в векторной и координатной форме их в уравнение неразрывности, получаем выражения:
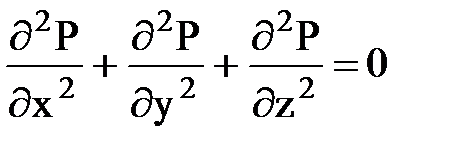 -
-
или в координатной форме;
или через дифференциальные операторы 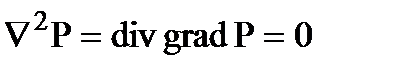
Это и есть дифференциальное уравнение установившейся фильтрации несжимаемой жидкости по закону Дарси, которое называется уравнением Лапласа. В теории фильтрации для удобства еще вводят функцию Ф(x, y, z), называемую потенциалом скорости фильтрации и определяемую как
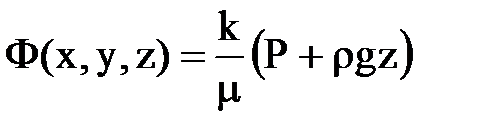 .
.
С ее помощью уравнение движения переходит в уравнение

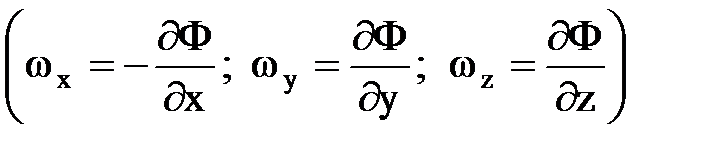 ,
,
а уравнение фильтрации -  .
.
Решениями уравнения Лапласа являются гармонические функции Р (x, y, z) и Ф (x, y, z), которые имеют непрерывные частные производные 1-го и 2-го порядка.
На решения уравнения Лапласа распространяется принцип суперпозиции, заключающийся в том, что если функции Ф1, Ф2 …Фn являются частными решениями, тогда их линейная комбинация
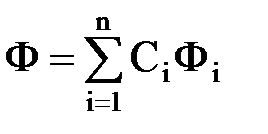 ,
,
где Сi – коэффициенты, также является решением. Это свойство широко используется при решении задач, сводящихся к уравнению Лапласа.
Дата добавления: 2017-02-20; просмотров: 2154;
