Фильтрационные течения несжимаемой жидкости в неоднородных пластах
Лекция № 14
3.7.1 Общие замечания.
В реальных условиях пористая среда редко бывает однородной. Неоднородной называется среда, у которой ее фильтрационные характеристики – пористость и проницаемость различны в различных точках. Однако часто даже в неоднородных пластах могут быть применены рассмотренные выше решения фильтрационных потоков, если эта неоднородность хаотичная (случайная). Тогда большие области пласта на макро уровне можно считать в среднем однородными. Но есть макро неоднородные пласты, в которых отдельные участки существенно различаются по фильтрационным характеристикам. В пластах-коллекторах нефти и газа выделяют следующие основные виды неоднородности.
1. Слоистая неоднородность. Фильтрационные характеристики в пределах слоев постоянны, а между собой различаются. При этом на границе пластов рассматривают два случая: слои гидравлически изолированы (границы непроницаемы) и между слоями существуют перетоки жидкости. Это случаи вертикальной неоднородности.
2. Зональная неоднородность, при которой пласт по площади распространения состоит из нескольких зон различной проницаемости. Это случай латеральной неоднородности.
3. Неоднородность, у которой проницаемость описывается непрерывной функцией от координат точек пространства k (x,y,z).
Рассмотрим одномерные потоки несжимаемой жидкости, подчиняющиеся закону Дарси в таких неоднородных пластах.
а) Слоистая неоднородность.
3.7.2 Прямолинейно-параллельный поток.
Горизонтальный пласт постоянной толщиной h и шириной В состоит из n пропластков с толщинами h1, h2…hn, проницаемостью k1, k2…kn и пористостью m1, m2…mn. На контуре давление - Рк; в скважинах - Рr (рис.14.1).

|
| ……… kn mn hn |
| k1 m1 h1 |
| k2 m2 h2 |
| k3 m3 h3 |
| h |
| Pk |
| x |
| Lk |
| Pr |
| а) |

|
| ° ° ° ° ° ° |
| w |
| B |
| Pk |
| Галерея скважин |
| Pr |
| контур питания |
| LK |
| б) |
| В |
Рис. 14.1. Разрез (а) и план пласта (б)
При отсутствии перетоков жидкости между пропластками распределение давления по координате х не будет зависеть от параметров среды и во всех пропластках будет одинаково. Оно будет аналогичным распределению давления в однородном пласте.
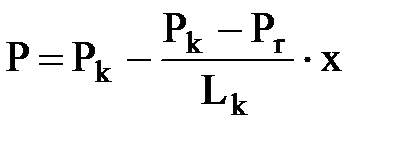 .
.
Скорость фильтрации в каждом i-м пропластке будет индивидуальной, т.к. зависит от проницаемости:
 , i = 1, 2 …n.
, i = 1, 2 …n.
Дебит потока Q можно вычислить как сумму дебитов в отдельных пропластках Qi:
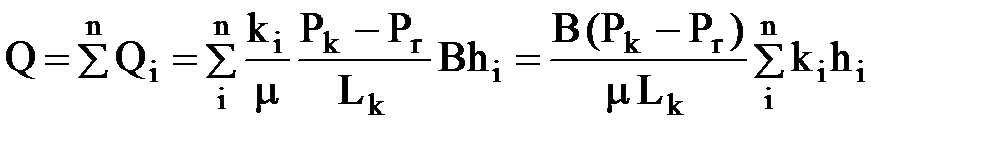 .
.
Движение частиц жидкости в каждом пропластке будет плоскопараллельным, но уравнения движения разные, из-за неодинаковой скорости фильрации
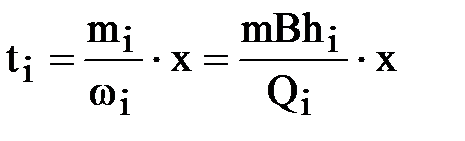 .
.
Для гидродинамических расчетов иногда бывает удобным заменить пласт со слоистой неоднородностью однородным пластом (h, B, Lk) со средневзвешенной проницаемостью, определенной на основе равенства дебитов.
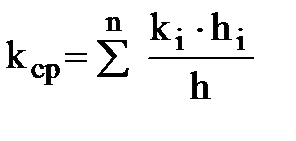 .
.
б) Зональная неоднородность.

| Рис. 14.2 |
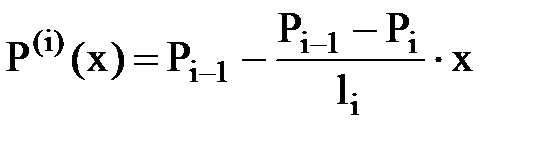 , li - 1< x< li,
, li - 1< x< li,
где: Р(i) (х) – распределение давления в i-й зоне, Рi-1 и Рi – давления на границах зон, играющие роль контурного и забойного давления в скважинах галереи соответственно.
Градиент давления в каждой зоне постоянный, но различный в разных зонах
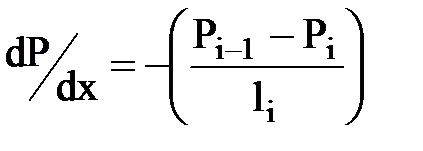 .
.
Дебит вследствие неразрывности потока несжимаемой жидкости будет постоянным в любом сечении потока (любой зоне).
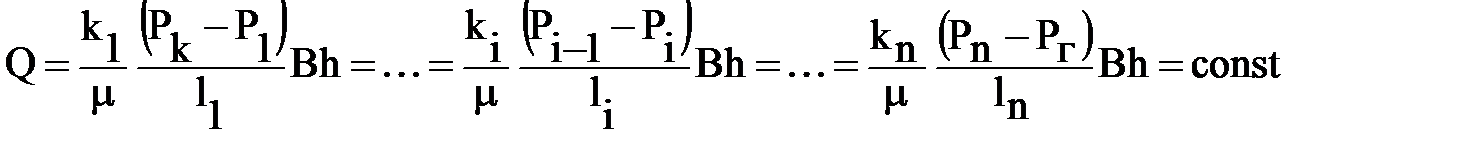
Применяя к потоку в i-й зоне свойства пропорций, получим выражение дебита через обобщенные характеристики пласта и граничные значения давлений
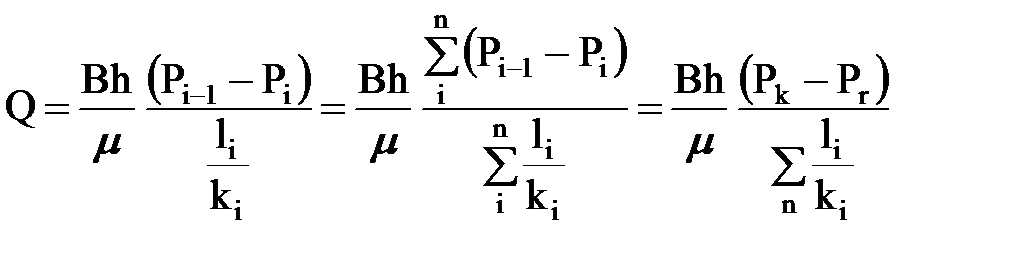 .
.
Скорость потока также постоянна в любом сечении
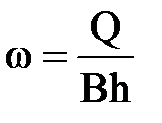 =const.
=const.
При этом надо иметь в виду, что истинные скорости движения частиц будут меньше в зонах с большей пористостью и наоборот.
Среднее значение проницаемости k ср такого неоднородного пласта определяется из равенства дебитов зонально - неоднородного и эквивалентного ему однородного пласта с проницаемостью k ср
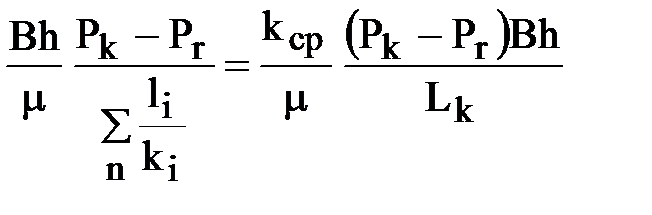 .
.
Отсюда
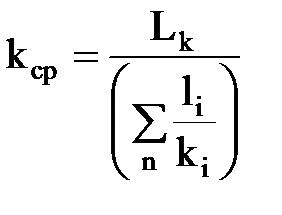 .
.
Давление pi на границе раздела сред с различной проницаемостью, входящие в формулу р(х), определим из условия равенства скоростей фильтрации в этих зонах:
 .
.
Например, если неоднородный пласт состоит из двух зон, как это часто бывает на практике, то
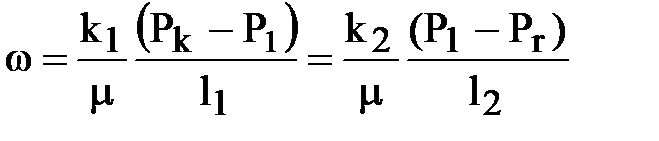 ,
,
отсюда 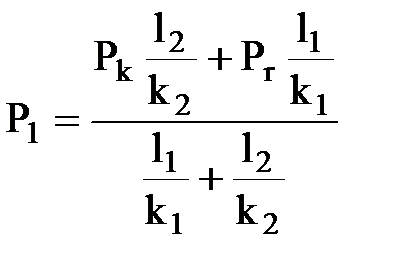 .
.
Теперь подставляя это решение в выражения распределения давления в зонах Р(1)(х) и Р(2)(х), найдем их выражения:
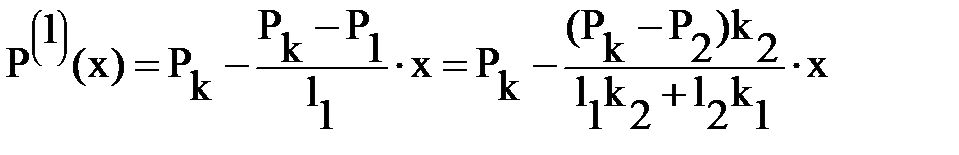 , 0 £ х £ l1,
, 0 £ х £ l1,
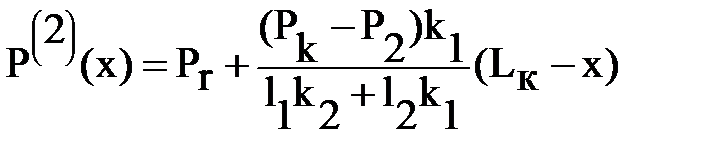 , l1 < x £ Lk.
, l1 < x £ Lk.
Если установившееся прямолинейное движение несжимаемой жидкости происходит в пласте, где проницаемость меняется непрерывно и задана функцией к = к (х), тогда дебит такого потока
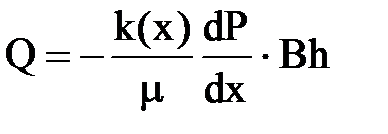 .
.
Разделяя переменные и интегрируя, получим
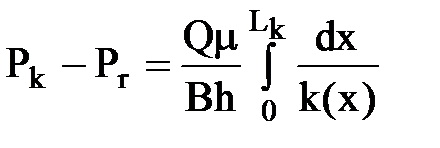 .
.
3.7.3. Плоскорадиальный поток.
а) Слоистая неоднородность.
| k1 m1 h1 k2 m2 h2 k3 m3 h3 ……… kn mn hn |
| Pr |
| Lk |
| h |
| Pk |
| P(r) P(r) |
| r |
| Рис. 14.3 |
Во всех пропластках распределение давления по цилиндрической координате r будет таким же как и для однородного пласта и подчиняться логарифмическому закону, поскольку граничные давления (Рк, Рс) в них одинаковы (рис. 14.3):
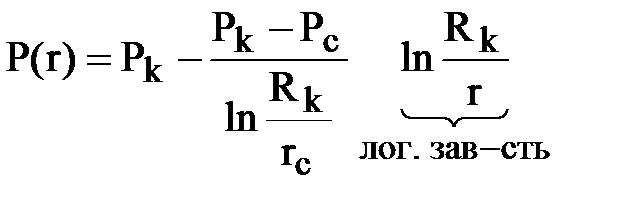 .
.
Градиент давления также одинаков:
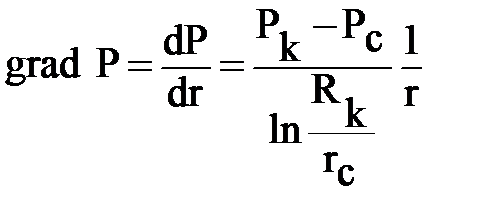 ,
,
Скорость фильтрации будет индивидуальной в каждом пропластке и пропорциональна его проницаемости - ki
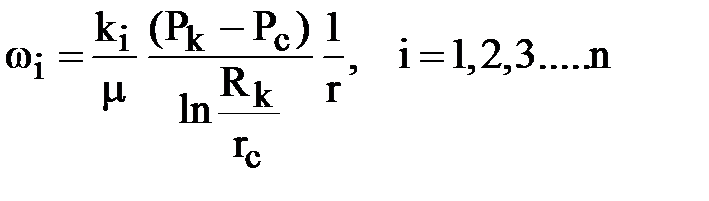 .
.
Дебит будет равен сумме дебитов пропластков:
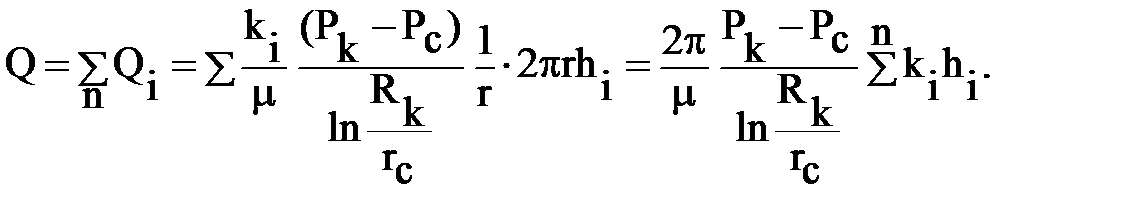
Средневзвешенное значение проницаемости можно определить из равенства дебитов слоисто-неоднородного и эквивалентного ему однородного пласта с проницаемостью кср:
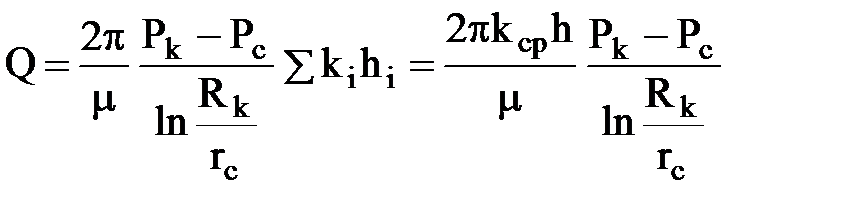 .
.
Откуда 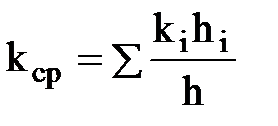 .
.
б) Зональная неоднородность.
| Rk ri ri-1 r |
| Имеется горизонтальный пласт (h, mi, ki, n, Рk, Рc) с кольцеобразными зонами, имеющими форму цилиндрических поверхностей, соосных со скважиной. На внешней n-й зоне, являющейся контуром питания пласта Rk, поддерживается постоянное давление Рk, на внутренней границе пласта rc (забое совершенной скважины) поддерживается постоянное давление Рс (рис. 14.4). |
Рис. 14.4
В пласте имеет место установившийся плоскорадиальный поток несжимаемой жидкости по закону Дарси.
Распределение давления в каждой i-й зоне будет подчиняться логарифмическому закону, где роль контурных давлений будут играть давления на внешних и внутренних границах зоны:
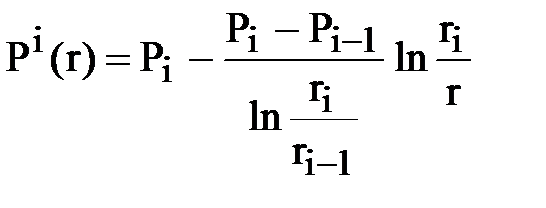 ; ri-1 £ r £ ri , i = 1, 2, …n,
; ri-1 £ r £ ri , i = 1, 2, …n,
где: Р(i)(r) – распределение давления в i-й зоне, Рi и Рi-1 – давления на границах зон, играющие роль контурного и забойного давления в скважине, соответственно (рис. 14.5).
| лог. закон |
| Pc |
| Pk |
| knmn kimi |
| rc |
| ri |
| ri-1 |
| h |
| k1m1 |
| · |
| Pk |
| Рис. 14.5 |
Градиент давления в каждой зоне также свой, но подчиняется гиперболическому закону
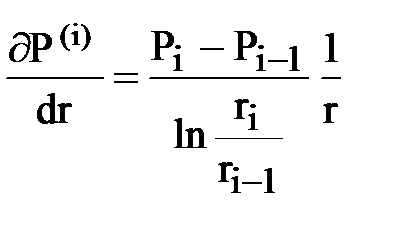 ; ri-1 < r £ ri , i = 1, 2, …n.
; ri-1 < r £ ri , i = 1, 2, …n.
Дебит потока вследствие неразрывности потока жидкости будет постоянным через любую цилиндрическую поверхность:
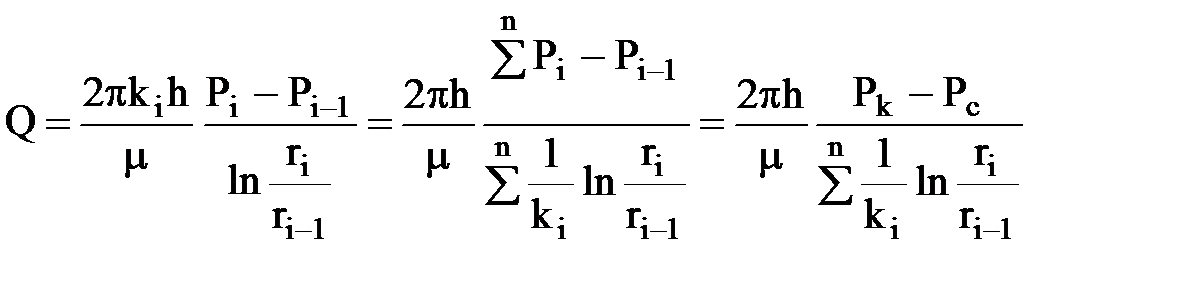 .
.
Скорость фильтрации в любой точке потока найдем как отношение дебита к соответствующему фильтрационному сечению пласта на координате r
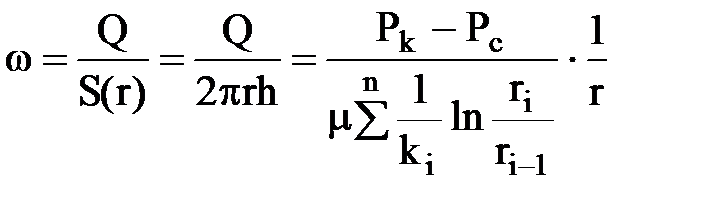 .
.
Среднее значение проницаемости определим, как обычно, из сопоставления дебита зонально-неоднородного пласта с дебитом эквивалентного ему однородного пласта:
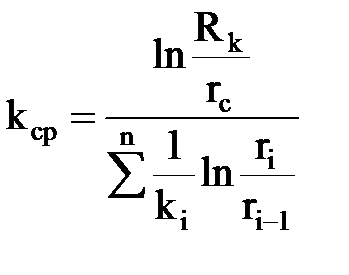 .
.
В практике разработки нефтяных месторождений значительный интерес представляет расчет параметров потока неоднородного пласта, состоящего из 2-х зон. Такая задача возникает при кислотной обработке призабойной зоны скважины, ее глинизации или парафинизации, установке гравийного фильтра и т.д. В этих случаях даже в однородном пласте вокруг скважины возникает кольцевая зона с отличными от внешней зоны параметрами (k, m). В этой связи очень важным бывает установить влияние проницаемости кольцевой призабойной зоны и остальной части пласта на ее продуктивность. Схема решения по определению распределения давления в зонах Р(1)(r) и Р(2)(r), а также дебита скважины аналогична рассмотренной ранее задачи для плоскопараллельного потока.
Определяют давление Р1 на границе 2-х зон исходя из равенства скорости фильтрации на их границе
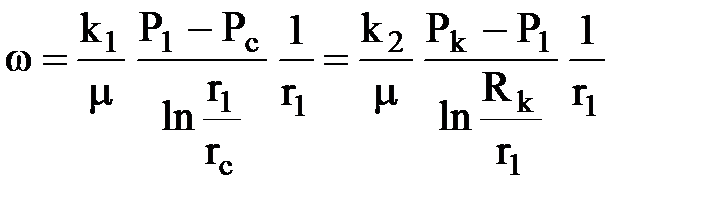 ;
;
откуда
 .
.
После этого находят Р(1)(r) и Р(2)(r) и дебит скважины.
Дата добавления: 2017-02-20; просмотров: 1250;
