Кирхгофтың екінші заңы бойынша
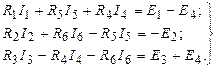 (1.29)
(1.29)
(1.28) теңдеулерді пайдаланып, (1.29) теңдеулерден шектес тармақтардағы 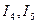 және
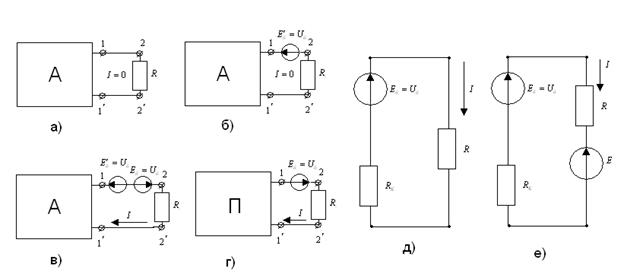
және 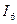 токтарды шығарып тастап табамыз:
токтарды шығарып тастап табамыз:
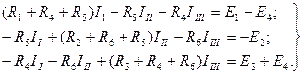 (1.30)
(1.30)
токтар әрбір контурға кіретін барлық тармақтардан өтеді, ал сол себептен оларды 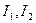 және
және 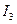 деп белгілеп контурлық токтар деп атаймыз.
деп белгілеп контурлық токтар деп атаймыз.
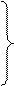 Контурға кіретін кедергілердің қосындысын контурдың өздік кедергісі деп атайды, ал бір уақытта екі немесе одан да көп контурларға жататын кедергіні жалпы кедергі деп атайды.
Контурға кіретін кедергілердің қосындысын контурдың өздік кедергісі деп атайды, ал бір уақытта екі немесе одан да көп контурларға жататын кедергіні жалпы кедергі деп атайды.
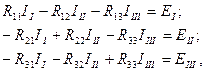 (1.31)
(1.31)
мұнда 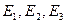 - контурлық ЭҚК-тер, яғни осы контурдағы әсер ететін ЭҚК-тердің алгебралық қосындысы.
- контурлық ЭҚК-тер, яғни осы контурдағы әсер ететін ЭҚК-тердің алгебралық қосындысы.
Теңдеулерге өздік кедергілер "+" таңбамен кіреді, ал жалпы кедергілер егер де кедергіден өтетін контурлық токтар бір-біріне қарсы бағытталса "-" таңбамен алынады.
Контурлық токтарды (1.30) теңдеулеурді шешкеннен кейін табамыз, ал содан кейін нақтылы токтарды анықтаймыз.
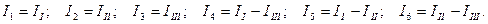
1.9 Активтік екі ұштықтан пассивтік екі ұштыққа максималды қуатты беру
Күрделі электр тізбектерді зерттеген кезде тек бір тармақтағы токпен, кернеумен және қуатпен қызығады. Және бөлек тармақты бөліп шығару электр энергияның көздері бар тізбектің бөлігімен қабылдағыштар бар бөлігімен байланысты табу үшін қолданады.
Екі бөлініп шыққан қысқыштары бар (ұштықтар деп аталады) ерекше кескін үйлесімді электр тізбектің бөлігін екі ұштық деп атайды. Электр энергия көздері бар екі ұштықты активтік , ал көздері жоқ екі ұштықты-пассивтік деп атаймыз. Әркім пассивтік екі ұштық электр энергияның тұтынушысы болады, сол себептен ішкі немесе кіріс кедергі Rк деп аталатын элементпен сипатталады.
Электр тізбектен бір 2-2` тармақты бөліп шығарайық. Оның кедергісі R және ол активтік екі ұштыққа қосылып тұр.
2-2` тармақтағы I тоқты табу үшін активтік екіұштықты ЭҚК көзімен және пассивтік екіұштықпен алмастыруға болатындықты көрсетейік.
1.15- сурет
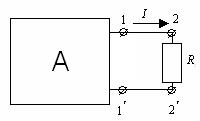
1.16 - сурет. Активтік екіұштықты кедергісі 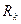 және
және 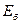 бар тармаққа түрлендіру.
бар тармаққа түрлендіру.
Көздің ЭҚК-терін табу үшін 1 және 2 нүктелер арасында тізбекті ажыратып жібереміз де 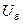 потенциалдар айырымын есептеумен немесе тәжірибе жолмен табамыз 1.16 - сурет. Содан кейін
потенциалдар айырымын есептеумен немесе тәжірибе жолмен табамыз 1.16 - сурет. Содан кейін 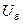 кері бағытталған
кері бағытталған 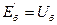 тең көзді 1 және 2 нүктеге қосамыз (1.16, б - сурет);
тең көзді 1 және 2 нүктеге қосамыз (1.16, б - сурет);
2-2` тармақтағы ток нөлге тең болып қала береді, себебі екі нүктенің арасындағы потенциалдар айырымы өзгерген жоқ.
1.16,б - суреттегі сүлбенің 1.15 - суреттегі сүлбеден айырмашылығы -1 және 2 нүктелерінің арасында 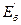 ЭҚК қосылған және 2-2` тармақтағы ток нөлге тең. Бұл сүлбе берілген сүлбеге баламалық болады, егер де 1 және 2 нүктелер арасына тағы бір
ЭҚК қосылған және 2-2` тармақтағы ток нөлге тең. Бұл сүлбе берілген сүлбеге баламалық болады, егер де 1 және 2 нүктелер арасына тағы бір 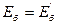 ЭҚК-ті кіргізсек.
ЭҚК-ті кіргізсек. 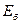 ЭҚК-тің бағыты
ЭҚК-тің бағыты 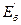 кері (1.16,в-сурет). Активтік екіұштық
кері (1.16,в-сурет). Активтік екіұштық 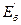 ЭҚК-пен қоса 2-2` тармақта токты тудырмайды (1.16, б - сурет). Сол себептен 2-2` тармақтағы
ЭҚК-пен қоса 2-2` тармақта токты тудырмайды (1.16, б - сурет). Сол себептен 2-2` тармақтағы 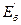 ЭҚК-пен құрылатын ток І бұл тармақтағы нақтылы токқа тең (1.16, г - сурет), яғни
ЭҚК-пен құрылатын ток І бұл тармақтағы нақтылы токқа тең (1.16, г - сурет), яғни
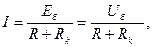 (1.32)
(1.32)
мұнда Rк-барлық ЭҚК-тер нөлге тең деп алғаннан кейін пассивтік екіұштықтың кіріс кедергісі.
Егер де қаралып жатқан тармақта кедергілермен бірге ЭҚҚ Е болса, онда бұл тармақтағы ток тең
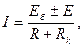 (1.33)
(1.33)
мұнда ЭҚҚ 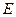 болымды (+), егер де оның бағыты
болымды (+), егер де оның бағыты 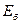 ЭҚК-пен бірдей болса, егер де бағыттары кері болса ЭҚҚ
ЭҚК-пен бірдей болса, егер де бағыттары кері болса ЭҚҚ 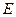 теріс (-) санмен жазылады.
теріс (-) санмен жазылады.
Пассивтік екі ұштықтың қуаты тең
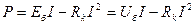 және
және 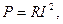 (1.34)
(1.34)
мұнда 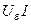 - активтік баламалық екіұштықтың қуаты:
- активтік баламалық екіұштықтың қуаты:
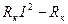 кедергiдегi куат шығыны.
кедергiдегi куат шығыны.
Құат Р максималды болатын кездегі І токты табу үшін (1.33) теңдеуден І бойынша Р-дан туындыны аламыз
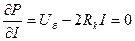 ,
,
ал бұдан ізделіп отырған ток
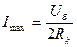
Жалпы жағдайда (2.15,д) ток 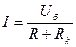 (1.35)
(1.35)
(1.35) теңдеуден шығады: қуат максималды егер де 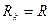 (1.36) яғни активтік. Бұл жағдайда екіұштықтың кіріс кедергісі және пассивтік екіұштықтың кедергісі тең (
(1.36) яғни активтік. Бұл жағдайда екіұштықтың кіріс кедергісі және пассивтік екіұштықтың кедергісі тең ( 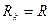 ).
).
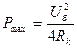 (1.36)
(1.36)
Активтік екі ұштықтың ПӘК тең
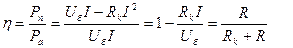 (1.37)
(1.37)
1.10 ЭҚК-тері және ток көздері бар тармақтар параллельді қосылғанда жүргізелетін түрлендіру
Егер де күрделі электр сұлбада бірнеше параллельді жалғанған ЭҚК көздері бар тармақтар болса, ол тармақтарды бір эквивалентті тармақпен ауыстырсақ, онда осындай сұлбаны есептеу және зерттеу жұмыстары әлдеқайда жеңілдейді.
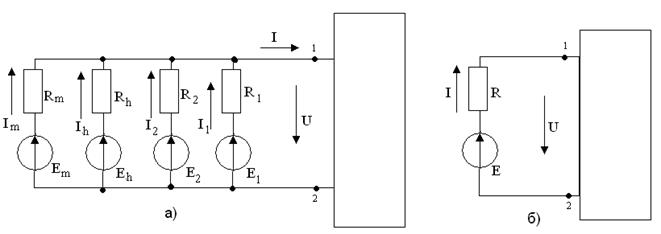
1.17 - сурет. Параллельді тармақтарды түрлендіру сүлбелер
Параллельді қосылған m тармақтарды бір тармаққа ауыстыру керек (1.17, б - сурет). Ол үшін ток І және кернеу U эквиваленті сүлбеде берілген сүлбедегідей қалу керек.
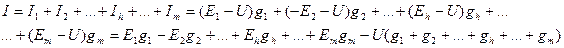
(1.38)
1.17, б - суреттегі сұлбада ток тең
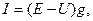 (1.39)
(1.39)
мұндағы 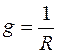 .
.
Эквиваленттік шарт орындалу үшін (1.38) және (1.39) теңдеулердің оң жақтарын теңестіріп, табамыз:
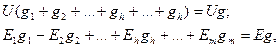 |
ал будан шығады
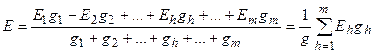

(1.40)
Егер де кейбір параллельді тармақтарда ЭҚК жоқ болса, онда (1.39)теңдеуде 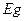 қосынды болмайды, бірақ
қосынды болмайды, бірақ 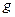 өткізгіштің ішіне бұл тармақтардың өткізгіштері кіреді.
өткізгіштің ішіне бұл тармақтардың өткізгіштері кіреді.
Егер де 1 және 2 түйіндерге ЭҚК-тердің көздері бар m тармақтардан басқа ток көздері бар n тармақ қосылса, онда
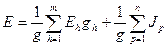
(1.41)
Егер де J бағыты эквивалентті Е бағытымен бірдей болса, онда болымды болып алынады, ал егерде болмаса -теріс болып алынады.
1.11 ЭҚК бар сүлбені эквивалентті ток көзі бар сүлбеге түрлендіру
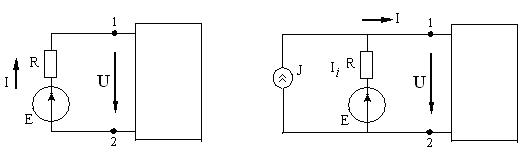
1.18 - сурет. ЭҚК-тің көзінен ток көзіне ауысу сұлбалары.
1.18,а - суретте ЭҚК-тің көзі R ішкі кедергісімен 1 және 2 қысқыштарға жалғанған, ал қысқыштар арасындағы кернеу U.
Ток І тең
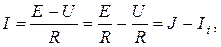 (1.42)
(1.42)

мұнда 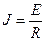 - ток көзінің тоғы;
- ток көзінің тоғы;
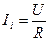 - ішкі кедергідегі ток;
- ішкі кедергідегі ток;
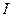 - ЭҚК-тің көзінің тоғы.
- ЭҚК-тің көзінің тоғы.
(1.42) теңдеуге 1.18,б - суреттегі эквивалентті сүлбе сәйкес. Бұл сүлбеде ток I және кернеу U 1.17,б - суреттегі сүлбедей.
Ток көзі тоғы J ЭҚК-тің бағытымен бір бағыттас.
1.12 Теңгеру (компенсация) жайындағы теорема
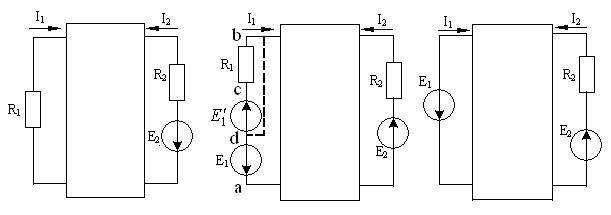
a) в) с)
1.19 - сурет. Теңгеру теоремасын түсіндіретін сүлбелер.
1.19, а - суретте көрсетілген электр сүлбеде кедергісі 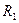 және тоғы
және тоғы 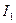 тең тармақ бөлінген.
тең тармақ бөлінген.
Осы тармаққа 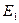 және
және 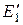 ЭҚК-тер көздерін енгіземіз.Олардың сан мәндері
ЭҚК-тер көздерін енгіземіз.Олардың сан мәндері 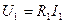 кернеуге және олардың бағыттары бір-біріне қарама қарсы алынған, ал сондықтан тоқтар барлық тармақтарда өзгермейді.
кернеуге және олардың бағыттары бір-біріне қарама қарсы алынған, ал сондықтан тоқтар барлық тармақтарда өзгермейді.
Кез келген кедергіні ЭҚК-тің көзіне ауыстыруға болады, оның бағыты ток бағытына қарама-қарсы және сол кедергідегі кернеуге тең. Мұны дәлелдеу үшін (1.19, б - сурет) " d " ,нүктеден " с " нүктеге өткенде потенциал 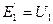 шамасына үлкейеді, ал "с" нүктеден "в" нүктеге өткенде сол шамаға азаяды. Осы салдарынан " d " және "b" нүктелерінің потенциалдары бір-біріне тең, яғни
шамасына үлкейеді, ал "с" нүктеден "в" нүктеге өткенде сол шамаға азаяды. Осы салдарынан " d " және "b" нүктелерінің потенциалдары бір-біріне тең, яғни 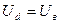 , ал сол себептен нүктелерді өткізгішпен тұйық қосуға болады. 1.18,б - суретте үзілмелі сызықпен көрсетілгендей, яғни тармақтың d-b бөлігін алып тастап 1.19, в - суретте көрсетілген сүлбеге келеміз, яғни
, ал сол себептен нүктелерді өткізгішпен тұйық қосуға болады. 1.18,б - суретте үзілмелі сызықпен көрсетілгендей, яғни тармақтың d-b бөлігін алып тастап 1.19, в - суретте көрсетілген сүлбеге келеміз, яғни 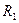 кедергіні
кедергіні 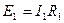 ЭҚК-пен алмастырдық.
ЭҚК-пен алмастырдық.
1.13 Беттесу әдістің принципі
Егер де (1.30) теңдеу жүйелерді анықтағыш арқылы шешкенде әрбір ток үшін, мысалы 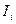 ток үшін, табамыз
ток үшін, табамыз
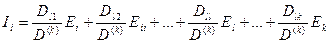 (1.43)
(1.43)
мұнда 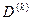 -(1.39) теңдеулер жүйесінің анықтағышы, ал
-(1.39) теңдеулер жүйесінің анықтағышы, ал 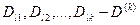 анықтағыштың алгебралық қосындылары.
анықтағыштың алгебралық қосындылары.
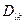 табу үшін
табу үшін 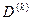 анықтағышта
анықтағышта 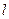 бағананы және
бағананы және 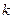 жолын сызып тастап көбейту керек.
жолын сызып тастап көбейту керек.
Егер де (1.43) теңдеуде барлық контурлық ЭҚК-терді тармақтардың ЭҚК-тердің алгебралық қосындысымен алмастырсақ, онда қосындыларды топтастырғаннан кейін 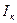 контурлық ток тармақтардың әрбір ЭҚК-пен қоздырылатын тоқ құрастырушылардың алгебралық қосындысы түрінде болады. Токтың әрбір құрастырушысы тармақтың ЭҚК-інің (1.43) теңдеуге кіретін коэффициенттерінің алгебралық көбейтіндісіне тең.
контурлық ток тармақтардың әрбір ЭҚК-пен қоздырылатын тоқ құрастырушылардың алгебралық қосындысы түрінде болады. Токтың әрбір құрастырушысы тармақтың ЭҚК-інің (1.43) теңдеуге кіретін коэффициенттерінің алгебралық көбейтіндісіне тең.
Бұл өте қажеті қасиет беттесу принципі деп аталады.
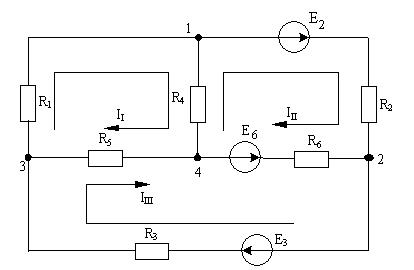
1.20 – сурет
Контурлық ток әдісімен келесі теңдеулерді жазамыз:
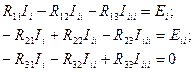 (1.45)
(1.45)
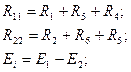
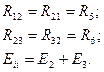
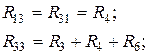
(1.45) шығады:
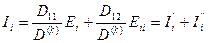 (1.46)
(1.46)
мұнда
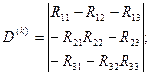
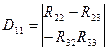
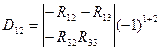
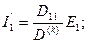
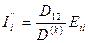 Сол сияқты
Сол сияқты 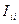 және
және 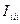 токтар табылады. Егер де (1.45) контурлық ЭҚК-терді тармақтардағы ЭҚК-термен алмастырсақ, онда табамыз:
токтар табылады. Егер де (1.45) контурлық ЭҚК-терді тармақтардағы ЭҚК-термен алмастырсақ, онда табамыз:
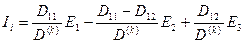 (1.47)
(1.47)
Сонымен, тармақтардағы токтарды табу үшін беттесу принципі арқылы сұлбада кезек-кезек бір ЭҚК-ті калдырып, ал басқа көздердің ЭҚК-терін нөлге тең деп аламыз, бірақ та сүлбеде олардың ішкі кедергілерін қалдырамыз.
Екінші тарау
2 Синусоидалы тоқтың бір фазалы электр тізбектері
2.1 Синусоидалы электр шамалар
Электр тізбекте кернеудің және тоқтың лездік шамалары тең уақыт аралық сайын қайталанатын процесс периодты деп аталады. Периодты шаманың мәні қайталанатын ең аз уақыты период деп аталады. Егер де 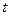 уақыттың периодты функциясын
уақыттың периодты функциясын 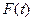 деп белгілесек, онда әрбір болымды немесе теріс
деп белгілесек, онда әрбір болымды немесе теріс 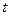 аргумент шама үшін мына теңдік әділетті болады:
аргумент шама үшін мына теңдік әділетті болады:
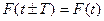 (2.1)
(2.1)
мұнда Т-период.
Периодқа кері шама, яғни уақыт бірлікте периодтардың саны жиілік деп аталады.
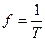 (2.2)
(2.2)
Жиілікті өлшеу бірлік – герц (Гц); егер де период 1с, онда жиілік 1 Гц тең.
Электр тізбектерде көбінесе периодты процестің түрі синусоидалды ереже, яғни барлық кернеулер және тоқтар бірдей жиіліктің синусоидалды функциялары болады.
2.1 - суретте синусоидалы функция көрсетілген.

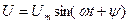 (2.3)
(2.3)
мұнда 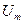 - максималды мәні немесе амплитуда;
- максималды мәні немесе амплитуда; 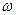 - аргументтің (бұрыштың) өзгеру жылдамдығы немесе бұрыштық жиілік; ол
- аргументтің (бұрыштың) өзгеру жылдамдығы немесе бұрыштық жиілік; ол 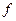 жиіліктің
жиіліктің 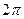 -ге көбейтіндісіне тең және рад/с- мен өлшенеді
-ге көбейтіндісіне тең және рад/с- мен өлшенеді
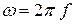 (2.3¹)
(2.3¹)
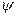 - басты фаза (координат басынан синусоиданың ығысуы).
- басты фаза (координат басынан синусоиданың ығысуы).
(2.1) функцияның аргумент ретінде уақыт 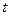 немесе сәйкесті бұрыш
немесе сәйкесті бұрыш 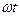 алынады.
алынады. 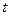 аргументке
аргументке 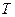 период сәйкес, ал аргумент
период сәйкес, ал аргумент 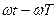 период сәйкес, аргумент және басты фаза
период сәйкес, аргумент және басты фаза 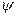 радианмен өлшенеді.
радианмен өлшенеді.
Егер де 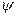 бұрыш градуспен өлшенсе, онда аргумент
бұрыш градуспен өлшенсе, онда аргумент 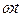 градусқа ауыстырылады (1 радиан=57,3°); бұл жағдайда период
градусқа ауыстырылады (1 радиан=57,3°); бұл жағдайда период 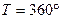 .
.
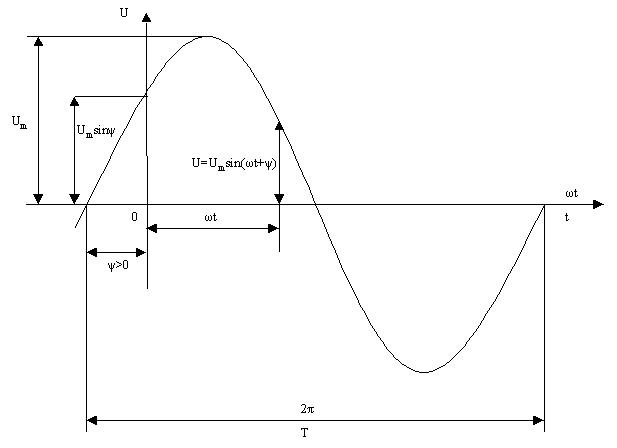
2.1-сурет
Синусоидалы шаманың өзгеріп тұрған мәнін белгілейтін шама 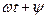 фаза деп аталады. Уақыт ағымы бойынша фаза өседі,
фаза деп аталады. Уақыт ағымы бойынша фаза өседі, 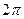 -шамаға фаза өскеннен кейін синусоидалды шаманың өзгеру циклі қайталанады.
-шамаға фаза өскеннен кейін синусоидалды шаманың өзгеру циклі қайталанады.
2.2 Синусоидалы функцияның орташа және әрекетті мәндері
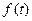 периодты функцияның
периодты функцияның 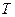 период ішінде орташа мәні мына кейіптемемен анықталады:
период ішінде орташа мәні мына кейіптемемен анықталады:
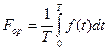 (2.4)
(2.4) 
Cинусоидалы функция кезде, болымды жартылай толқынның ауданы теріс жартылый толқынның ауданымен өтемеленеді, ал сол себептен период ішіндегі орташа мән нөлге тең. Сондықтан жартылай периодтың мәнін, яғни синусоиданың болымды жартылай толқынын алады.
Бұған сәйкес, амплитудасы 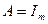 cинусоидалы тоқтың орташа мәніне тең:
cинусоидалы тоқтың орташа мәніне тең:
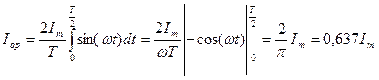 (2.5)
(2.5)
Кернеудің орташа мәні
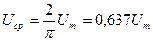 (2.6)
(2.6)
Тоқтың жылулық әсері және екі сымның , олар арқылы бірдей тоқ өткенде, өзара әсерлік механикалық күш тоқтың шаршысына пропорционалды. Сондықтан, тоқтың мәнін период бойы әрекетті мәнімен белгіленеді.
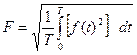 (2.7)
(2.7)
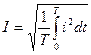 (2.8)
(2.8)
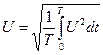 (2.9)
(2.9)
Синусоидалы тоқ кезде
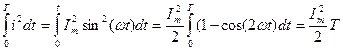
(2.8.) кейіптеме бойынша
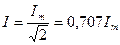 (2.10)
(2.10)
Әрекетті синусоидалы кернеу
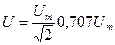 (2.11)
(2.11)
Электротехникалық құрылғылардың номиналды тоғы және кернеуі әрекетті мәндерімен белгіленеді.
Әрекетті мәндерді өлшеу үшін жылулық, электромагниттік, электродинамикалық және т.б. аспаптар жүйелері қолданылады.
2.3 Кедергідегі синусоидалы тоқ
Егер де R кедергіге синусоидалы кернеу 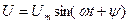 ынта салынса, онда кедергі арқылы мынадай синусоидалды тоқ ағады:
ынта салынса, онда кедергі арқылы мынадай синусоидалды тоқ ағады:
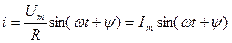 (2.12)
(2.12)
Демек, кедергінің шықпаларындағы кернеу және одан өтіп жатқан тоқтың басты фазалары бірдей (фаза бойынша тура келеді): олар бір мезгілде өздерінің амплитудалық 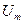 және
және 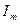
 мәндеріне жетеді және бір мезгілде нөлден өтеді (2.2-сурет).
мәндеріне жетеді және бір мезгілде нөлден өтеді (2.2-сурет).
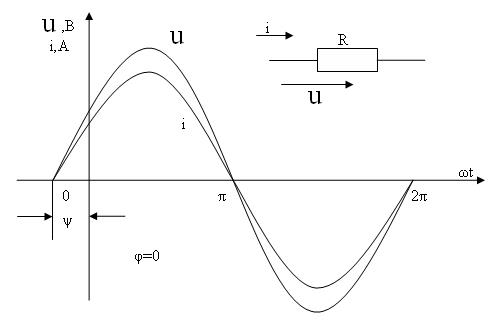
2.2-сурет. Кедергідегі синусоидалы кернеу және тоқ.
Жиіліктері бірдей екі синусоиданың басты фазаларының айырымы фазалық ығысу деп аталады. Бұл жағдайда фазалық ығысу кернеумен тоқтың арасында нөлге тең:
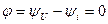 (2.13)
(2.13)
Кедергі 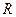 арқылы синусоидалды тоқ өткен кезде амплитуталар және кернеудің, тоқтың әрекетті мәндері Ом заңымен байланысқан, яғни
арқылы синусоидалды тоқ өткен кезде амплитуталар және кернеудің, тоқтың әрекетті мәндері Ом заңымен байланысқан, яғни
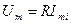 ;
; 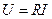
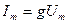 ;
; 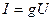 (2.14)
(2.14)
Кедергіге түсетін лезді қуат:
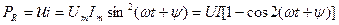 ,тоқтың және кернеудің жиілігіне қарағанда екі есе бұрыштық жиілікпен өзгереді. Тербелiну шектері 0-ден
,тоқтың және кернеудің жиілігіне қарағанда екі есе бұрыштық жиілікпен өзгереді. Тербелiну шектері 0-ден 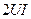 -ге дейін (2.3 -сурет.)
-ге дейін (2.3 -сурет.)
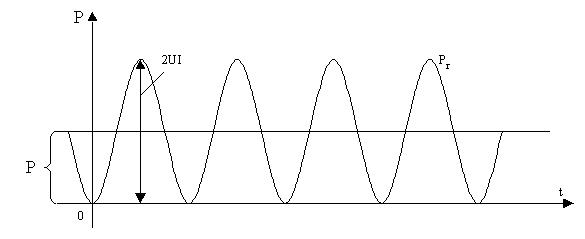
2.3 –сурет. Кедергіге түсетін лезді қуат 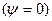
PR қисығы екі қосындылардан құралады: тұрақты қосынды P=UI және амплитудасы UI, ал жиілігі 2 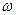 тең косинусойдалды функциядан.
тең косинусойдалды функциядан.
Период ішіндегі орташа қуаттың мәні активтік қуат деп аталады да, ол тең: 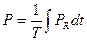 (ваттпен өлшенеді).
(ваттпен өлшенеді).
Қаралып отырған жағдайда 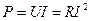 .
.
Кедергіні активтік қуаттың тоқтың шарашы шамасына қатынасы деп белгілеуге болады 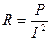 .
.
Айнымалы тоқ кездегі активтік кедергі деп аталады.
2.4 Индуктивтіктегі синусоидалды тоқ
Егер де L индуктивтік арқылы синусоидалды тоқ 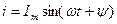 өтсе, онда өздік индукцияның электр қозғаушы күш тең:
өтсе, онда өздік индукцияның электр қозғаушы күш тең:
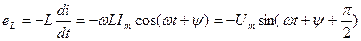 (2.16)
(2.16)
Демек, индуктивтіктегі кернеу:
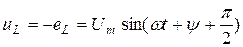 (2.17)
(2.17)
(2.17) кейіптемеден шығады: индуктивтіктегі кернеу тоқты 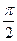 (немесе 90°) бұрышқа озып отырады; кернеудің максимумы тоқтың максимумынан солға қарай 90°-қа ығысады (2.4-сурет).
(немесе 90°) бұрышқа озып отырады; кернеудің максимумы тоқтың максимумынан солға қарай 90°-қа ығысады (2.4-сурет).


2.4-сурет. Индуктивтіктегі синусоидалы кернеу және тоқ
Фазалық ығысу:
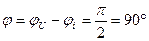 (2.18)
(2.18)
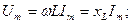
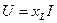 (2.19)
(2.19)
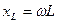 - индуктивтік кедергі, ал оған кері шама
- индуктивтік кедергі, ал оған кері шама 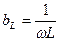 - индуктивтік өткізгіштік деп аталады. Сонымен,
- индуктивтік өткізгіштік деп аталады. Сонымен, 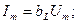
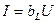 (2.20)
(2.20)
Индуктивтіктегі лезді қуат тең:
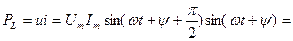
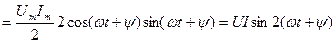 (2.21)
(2.21)
Бұл қуат амплитудасы 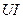 , ал бұрыштық жиілігі
, ал бұрыштық жиілігі 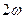 тең синусоидалды заң бойынша тербеленеді.
тең синусоидалды заң бойынша тербеленеді.
Индуктивтіктің магнит өрісінің энергиясы:
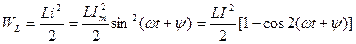 (2.22)
(2.22)
0 ден 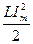 -ге дейін шектерде бұрыштық жиілігі
-ге дейін шектерде бұрыштық жиілігі 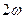 -мен периодикалы өзгеріп тұрады (2.5-сурет).
-мен периодикалы өзгеріп тұрады (2.5-сурет).


2.5-сурет. Индуктивтіктегі лезді қуат және өрістің энергиясы.
Көзбен және индуктивтіктің арасында энергияның тербелісі өтеді, ал индуктивтікке түсетін активтік қуат нөлге тең. Индуктивтік кедергіні былай табуға болады: 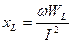 (2.23)
(2.23)
2.5 Сыйымдылықтағы синусойдалы тоқ
Егер де 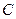 сыйымдылықтағы кернеу синусойдалды болса (2.6-сурет)
сыйымдылықтағы кернеу синусойдалды болса (2.6-сурет)
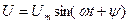 , онда тоқ:
, онда тоқ:
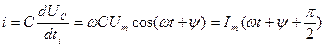 (2.24)
(2.24)
(2.24) көрініс көрсетіп тұр: тоқ 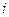 ынта салынған кернеуден
ынта салынған кернеуден 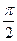 бұрышқа озып тұр, яғни тоқтың нөлдік мәніне кернеудің максималды мәні сәйкес.
бұрышқа озып тұр, яғни тоқтың нөлдік мәніне кернеудің максималды мәні сәйкес.


2.6-сурет. Сыйымдылықтағы синусойдалы кернеу және тоқ.
Фазалық ығысу: 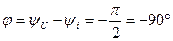 (2.25)
(2.25)
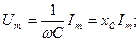
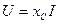 (2.26)
(2.26)
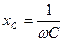 -сыйымдылық кедергі, ал оған кері шама
-сыйымдылық кедергі, ал оған кері шама 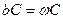 -сыйымдылық өткізгіштік деп аталады. Сонымен,
-сыйымдылық өткізгіштік деп аталады. Сонымен, 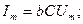
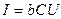 (2.27)
(2.27)
Сыйымдылықтағы лезді қуат:
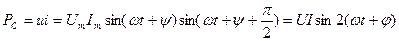 (2.28)
(2.28)
Бұл қуат амплитудасы 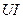 , ал бұрыштық жиілігі
, ал бұрыштық жиілігі 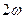 тең синусойдалды заң бойынша тербеленеді, яғни көрініс
тең синусойдалды заң бойынша тербеленеді, яғни көрініс 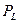 сияқты.
сияқты.
Сыйымдылықтың электр өрісінің энергиясы:
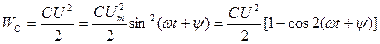 (2.29)
(2.29)
0-ден 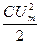 -ге дейін шектерде бұрыштық жиілігі
-ге дейін шектерде бұрыштық жиілігі 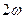 -мен периодикалы өзгеріп тұрады.
-мен периодикалы өзгеріп тұрады.
Көзбен сыйымдылықтың арасында энергияның тербеленуі өтеді, ал сыйымдылыққа түсетін активтік қуат нөлге тең. Сыйымдылық кедергіні былай табуға болады: 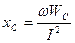 (2.30)
(2.30)
2.6R,L және C элементердің тізбектеп қосылуы
Тізбектеп қосылған R,L және C элементерден құралған электр тізбектен 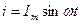 синусойдалды тоқ өткенде (2.7-сурет)
синусойдалды тоқ өткенде (2.7-сурет)
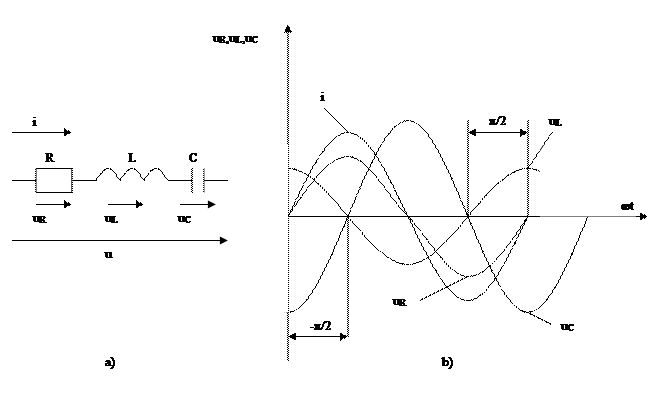

2.7-сурет. Тізбектеп қосылған кедергіде, индуктивтікте және
сыйымдылықта синусойдалы тоқ кездегі кернеулер.
бұл тізбектің шықпаларында бөлек элементтердегі синусойдалды кернеулердің қосындысына тең синусойдалы кернеу қурылады [Кирхгофтың екінші заңы]:
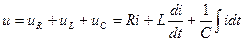 (2.31)
(2.31)
Тізбектің шықпасындағы 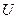 кернеу тең:
кернеу тең:
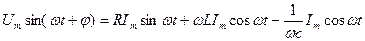
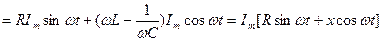 (2.32)
(2.32)
(2.32) теңдеу лезді кернеулер үшін Кирхгофтың екінші заңының жазылуының тригонометриялық түрі. Бұған кіретін шама 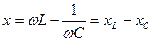 -тізбектің реактивтік кедергісі деп аталады. Бұл кедергі таңбаға қарай
-тізбектің реактивтік кедергісі деп аталады. Бұл кедергі таңбаға қарай 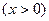 болса индуктивтік, ал
болса индуктивтік, ал 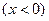 болса сыйымдылық түрлі болады.
болса сыйымдылық түрлі болады.
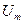 және
және 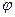 табу үшін келесі тригонометриялық қатынастарды пайдаланамыз:
табу үшін келесі тригонометриялық қатынастарды пайдаланамыз:
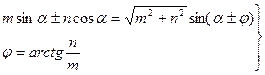 (2.33)
(2.33)
Сонымен,
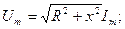
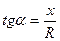 (2.34)
(2.34)
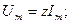
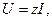 мұнда
мұнда 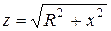 -тізбектің толық кедергісі.
-тізбектің толық кедергісі.
Тізбектеп 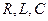 қосылған тізбектің шықпаларындағы кернеу
қосылған тізбектің шықпаларындағы кернеу 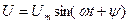 белгілі болса, онда тізбектен ағып тұрған тоқ:
белгілі болса, онда тізбектен ағып тұрған тоқ:
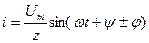 (2.35)
(2.35)
Тізбектің түрі индуктивтік болса бұрыш 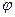 болымды
болымды 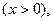 ал сыйымдылық болса-теріс
ал сыйымдылық болса-теріс 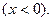
Тізбектің активтік және реактивтік кедергілердің толық кедергімен байланысы:
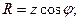
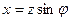 (2.36)
(2.36)
Кернеудің активтік және реактивтік құрастырушылары:
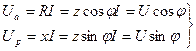
Тізбектің толық кернеуі:
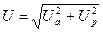 (2.37)
(2.37)
2.7R,L және C элементтердің параллельді қосылуы
Егер де 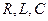 элементтер параллельді қосылған тізбекке (2.8-сурет) синусойдалды кернеу
элементтер параллельді қосылған тізбекке (2.8-сурет) синусойдалды кернеу 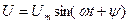 ынта салынса, онда бұл тізбектен өткен тоқ параллельді тармақтардан өтетеін тоқтардың алгебралық қосындысына тең [Кирхгофтың бірінші заңы]:
ынта салынса, онда бұл тізбектен өткен тоқ параллельді тармақтардан өтетеін тоқтардың алгебралық қосындысына тең [Кирхгофтың бірінші заңы]:
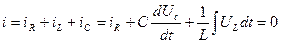 (2.38)
(2.38)


2.8-сурет. Синусойдалы кернеу кезде параллельді қосылған кедергіде, индуктивтікте және сыйымдылықтағы тоқтар.
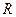 кедергідегі
кедергідегі 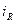 тоқ
тоқ 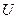 кернеумен фаза бойынша біртектес,
кернеумен фаза бойынша біртектес, 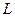 индуктивтіктегі
индуктивтіктегі 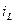 тоқ
тоқ 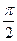 бұрышқа қалады, ал
бұрышқа қалады, ал 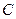 сыйымдылықтағы
сыйымдылықтағы 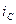 тоқ
тоқ 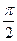 бұрышқа
бұрышқа 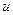 кернеуден озады (2.8-сурет).
кернеуден озады (2.8-сурет).
Тізбектегі қосындысы (жалпы) тоқ тең:
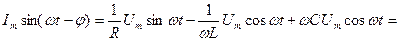
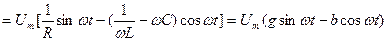 (2.39)
(2.39)
(2.39) теңдеу лездік тоқтар үшін Кирхгофтың бірінші заңының жазылуының тригонометриялық түрі. Бұған кіретін шама 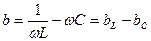 -тізбектің реактивтік өткізгіштігі деп аталады. Бұл өткізгіштік таңбаға қарай
-тізбектің реактивтік өткізгіштігі деп аталады. Бұл өткізгіштік таңбаға қарай 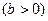 индуктивтік, ал
индуктивтік, ал 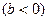 сыйымдылық түрлі болады.
сыйымдылық түрлі болады.
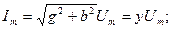
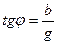 (2.40)
(2.40)
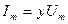 немесе
немесе 
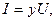 мұнда
мұнда 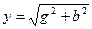 -тізбектің толық өткізгіштігі.
-тізбектің толық өткізгіштігі.
Тоқ 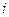 кернеу
кернеу 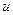 -дан бұрыш
-дан бұрыш 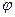 -ға не қалады, не озады.
-ға не қалады, не озады.
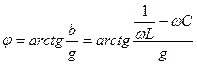
Егер де тізбектің шықпаларында кернеу 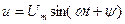 берілген болса, онда тізбектегі тоқ тең:
берілген болса, онда тізбектегі тоқ тең:
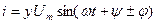 (2.41)
(2.41)
Тізбектің түрі индуктивтік болса бұрыш 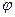 болымды
болымды 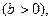 ал сыйымдылық болса теріс
ал сыйымдылық болса теріс 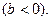
Тізбектің активтік және реактивтік өткізгіштіктердің толық өткізгішпен байланысы:
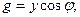
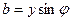 (2.42)
(2.42)
Тоқтың активтік және реактивтік құрастырушылары:
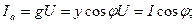
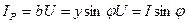 (2.43)
(2.43)
Тізбектің толық тоғы: 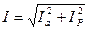
2.8Синусоидалды тоқ тізбектегі қуат
Тізбектің кернеуі 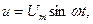 ал тоғы
ал тоғы 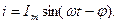
Лезді қуат:
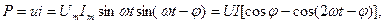 (2.44)
(2.44)
яғни екі бөліктен құралады: тұрақты шама 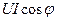 және кернеумен тоқтың жиіліктерінен екі есе үлкен синусойдалды шамадан.
және кернеумен тоқтың жиіліктерінен екі есе үлкен синусойдалды шамадан.
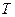 уақыт ішінде екінші қосындының орташа мәні нөлге тең. Сондықтан тізбектегі активтік қуат:
уақыт ішінде екінші қосындының орташа мәні нөлге тең. Сондықтан тізбектегі активтік қуат:
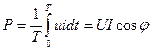 (2.45)
(2.45)
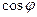 -қуат коэффициент деп аталады.
-қуат коэффициент деп аталады.
Активтік қуат басқа түрде көрсетуге болады:
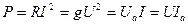 (2.46)
(2.46)
Кедергі және индуктивтігі бар тізбекті қарап шығайық. Бұл жағдайда 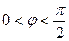 және
және 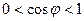 .
.
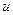 және
және 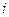 таңбалары бірдей кездегі уақыт аралықта лезді қуат болымды; энергия көзден қабылдағышқа түседі де кедергіде жұтылады және индуктивтіктің магнит өрісінде қолданады.
таңбалары бірдей кездегі уақыт аралықта лезді қуат болымды; энергия көзден қабылдағышқа түседі де кедергіде жұтылады және индуктивтіктің магнит өрісінде қолданады.
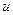 және
және 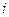 таңбалары кері кездегі уақыт аралықта лезді қуат теріс; энергияның бір бөлігі (магнит өрістегі) көзге қайтады. Активтік – сыйымдылық тізбекте көрініс ұқсас болады
таңбалары кері кездегі уақыт аралықта лезді қуат теріс; энергияның бір бөлігі (магнит өрістегі) көзге қайтады. Активтік – сыйымдылық тізбекте көрініс ұқсас болады 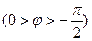 .
.


2.9-сурет. Активтік – индуктивтік тізбекке түсетін қуат.
Шінші тарау
3 Комплексті сандарды және векторлық диаграммаларды электр тізбектерді есептеуге қолдану
3.1 Синусоидалы функцияларды айнымалы векторлардың проекциялары түрінде көрсету
Электр тізбек күрделенгенде тригонометриялық түрде есептеу қиындап кетеді, ал сол себептен тұрақты тоқ тізбектерге ұқсасты айнымалы тоқ тізбектерді алгебралық түрде есептеуге рұқсат ететін әдіс керек болады. Мұндай ыңғайлы әдіс ретінде синусойдалы функцияларды құрауды айнымалы векторларды қарауға ауыстыруға орнатылған комплексті әдіс.
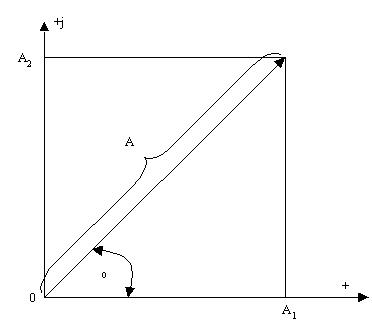 |
Комплексті жазықтықта әрбір нүкте бұл нүктені радиус-векторымен белгіленеді. Вектордың басы координат басымен үйлеседі, ал аяғы берілген комплексті санға сәйкесті нүктеде жатады (3.1-сурет).
3.1-сурет. Комплексті санды бейнейлейтін вектор.
Комплексті санды көрсеткіш немесе полярлы түрде жазуға болады:
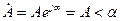 (3.1)
(3.1)
мұнда 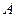 -модуль;
-модуль; 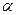 -аргумент немесе фаза;
-аргумент немесе фаза; 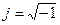
Комплексті санның тригонометриялық түрде жазылуы:
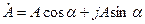 (3.2)
(3.2)
және оның алгебралық түрі:
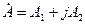 (3.3)
(3.3)
мұнда 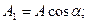
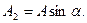
Демек,
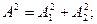
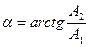 (3.4)
(3.4)
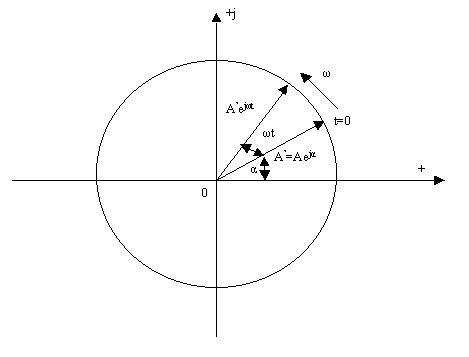
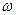 бұрыштық жылдамдықпен болымды бағытпен, яғни сағат тіліне қарсы, айналып тұрған векторды былай көрсетуге болады:
бұрыштық жылдамдықпен болымды бағытпен, яғни сағат тіліне қарсы, айналып тұрған векторды былай көрсетуге болады:
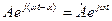 (3.5)
(3.5)
мұнда 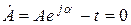 уақыт мезгілде векторды көрсететін комплекстіамплитуда (3.2-сурет). Басқаша айтқанда, бұл уақыттан тәуелсіз, модуль және аргументы берілген синусоидалды функцияның амплитудасына және басты фазасына тең комплексті шама.
уақыт мезгілде векторды көрсететін комплекстіамплитуда (3.2-сурет). Басқаша айтқанда, бұл уақыттан тәуелсіз, модуль және аргументы берілген синусоидалды функцияның амплитудасына және басты фазасына тең комплексті шама.
 |
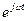 көбейткіш – айналдыру оператор. Комплексті амплитуда
көбейткіш – айналдыру оператор. Комплексті амплитуда 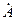 -ны
-ны 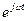 көбейту болымды бағытқа вектор
көбейту болымды бағытқа вектор 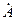 -ны бұрыш
-ны бұрыш 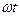 бұруды көрсетеді.
бұруды көрсетеді.
3.2-сурет. Айналмалы вектор.
(3.5) функцияны тригонометриялық түрде жазғанда шығады:
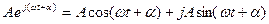
Қорытқанда, 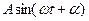 синусоидалды функция
синусоидалды функция 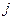 көбейткішсіз алынған комплексті (3.5) функцияның жорымал бөлігі немесе айналмалы вектордың жорамалды білікке проекциясы.
көбейткішсіз алынған комплексті (3.5) функцияның жорымал бөлігі немесе айналмалы вектордың жорамалды білікке проекциясы.
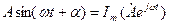 (3.6)
(3.6)
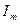 -комплексті функцияның жорамал бөлігі алынғанын көрсетеді.
-комплексті функцияның жорамал бөлігі алынғанын көрсетеді.
Егер де синусоидалды функциялардың жиіліктері бірдей болса, онда бұл функцияларға сәйкесті векторлар бірдей бұрыштық жылдамдықпен айналады, ал сол себептен олардың арасындағы бұрыштар өзгермейтін болып сақталады.
3.3,а-суретте бұрыштық жиіліктері 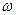 бірдей екі синусойдалды функциялар
бірдей екі синусойдалды функциялар 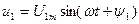 және
және 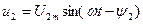 көрсетілген. Функция
көрсетілген. Функция 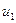 фаза бойынша функция
фаза бойынша функция 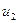 -деп озып тұр, фазалық ығысу басты фазалардың айырымына тең:
-деп озып тұр, фазалық ығысу басты фазалардың айырымына тең:
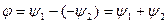
3.3,b-суретте бұл бұрышты өздері ара векторлар құрып тұр.
Басты фазалар тең кезде, яғни фазалық ығысу нөлге тең болғанда, векторлар бір жаққа бағытталады (фаза бойынша біртектес).
Фазалық ығысу 180° болғанда векторлар қарама-қарсы жақтарға бағытталады (қайшы фазада болады).
Фаза бойынша олардың өзара бағытта болуды сақтаумен құрылған векторлардың жиынтықтарын бейнелейтін диаграмма векторлық диаграмма деп аталады.
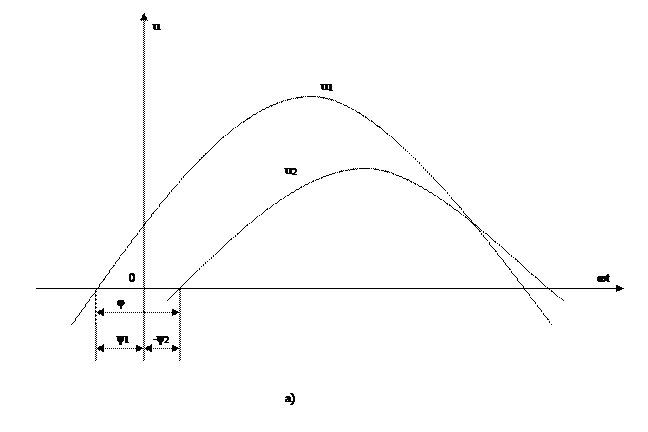

3.3-сурет
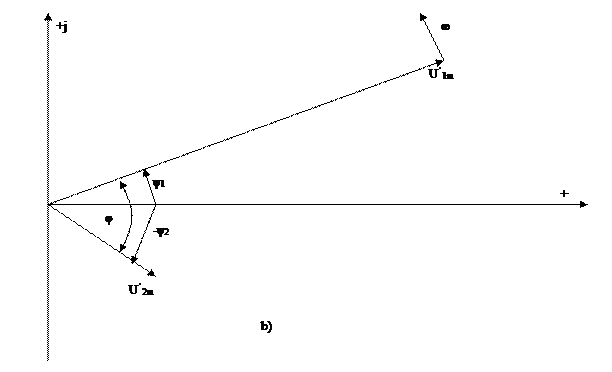

3.3-сурет
3.2 Комплекстік түрдегі Ом және Кирхгофтың заңдары
а) 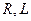 және
және 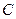 -нің тізбектеп қосылуы
-нің тізбектеп қосылуы
Кирхгофтың екінші заңы бойынша жазылған теңдеуде
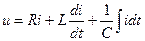 (3.7)
(3.7)
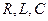 параметрлар және кернеу
параметрлар және кернеу 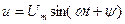 берілген болсын, ал ізденіп жатқан шама – тоқ.
берілген болсын, ал ізденіп жатқан шама – тоқ.
(3.7) дифференциалды теңдеудің шешуі синусоидалды функцияны береді,
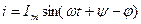 ,
,
мұнда 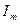 және
және 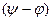 -тоқтың әлі белгісіз амплитудасы және басты фазасы, берілген синусоидалы кернеуге комплексті функция
-тоқтың әлі белгісіз амплитудасы және басты фазасы, берілген синусоидалы кернеуге комплексті функция 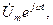 ал ізденіп жатқан синусоидалды тоққа-комплексті функция
ал ізденіп жатқан синусоидалды тоққа-комплексті функция 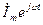 сәйкесті болады.
сәйкесті болады.
Онда (4.7) теңдеуді мына түрде көрсетуге болады,
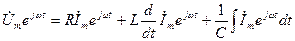 (3.8)
(3.8)
Дифференциалдайды және интегралдауды өткізіп, табамыз;
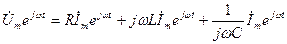 (3.9)
(3.9)
(3.9) теңдеудің барлық бөліктерін көбейткіш 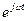 қысқартып алгебралық комплексті теңдеуді табамыз:
қысқартып алгебралық комплексті теңдеуді табамыз:
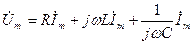 (3.10)
(3.10)
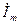 тоқты жақшаның сыртына шығарғанда, болады:
тоқты жақшаның сыртына шығарғанда, болады:
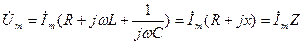 (3.11)
(3.11)
мұнда 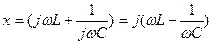 -реактивтік кедергі; (3.12)
-реактивтік кедергі; (3.12)
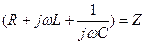 -комплексті толық кедергі (3.13)
-комплексті толық кедергі (3.13)
(3.11) теңдеудің екі жағы 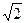 бөлсек, комплексті әсерлік мәндер үшін Омның заңын шығарамыз,
бөлсек, комплексті әсерлік мәндер үшін Омның заңын шығарамыз,
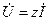 (3.14)
(3.14)
Комплексті кедергіні тригонометриялық және көрсеткіш түрлері,
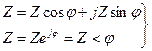 (3.15)
(3.15)
мұнда 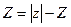 -комплексті санның модулі, ал
-комплексті санның модулі, ал 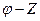 комплексті санның аргументі,
комплексті санның аргументі,
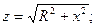
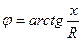 (3.16)
(3.16)
(3.11) теңдеу бойынша тоқтың комплексті амплитудасы
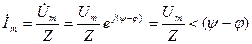
мұнда 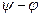 -тоқтың басты фазасы.
-тоқтың басты фазасы.
Олай болса, ізденіп жатқан тоқ тригонометриялы түрде
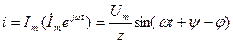 (3.17)
(3.17)
бұл бұрынғы табылған (2.35) теңдеумен бірдей болып шықты яғни нәтижелерді бір-бірімен толық біртектес.
3.4-суретте (3.13) теңдеудің комплекті жазықтықта геометриялық талдау берілген. 3.4,а-сурет тізбектің реактивтік кедергісі индуктивтік түріне жатады 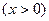 , ал оған сәйкес тоқ кернеуден фаза бойынша қалып қалады
, ал оған сәйкес тоқ кернеуден фаза бойынша қалып қалады 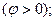 3.4,б-сурет тізбектің реактивтік кедергісі сыйымдылық түріне жатады
3.4,б-сурет тізбектің реактивтік кедергісі сыйымдылық түріне жатады 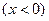 , ал оған сәйкес тоқ кернеуден фаза бойынша озып кетеді
, ал оған сәйкес тоқ кернеуден фаза бойынша озып кетеді 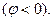
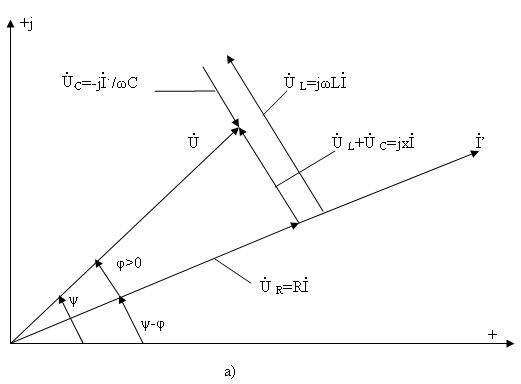
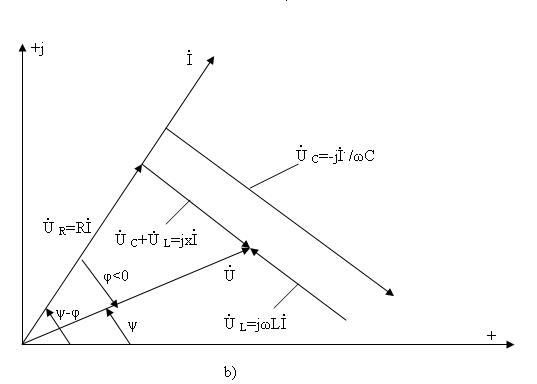
3.4-сурет. 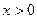 (а) және
(а) және 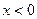 (b) кезде
(b) кезде 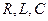 тізбекті қосылған
тізбекті қосылған
үшін векторлық диаграммалар.
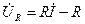 кедергідегі кернеу (
кедергідегі кернеу ( 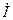 тоқпен біртектес),
тоқпен біртектес), 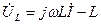 индуктивтіктегі кернеу (
индуктивтіктегі кернеу ( 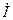 тоқтан 90° бұрышқа қалып қалады).
тоқтан 90° бұрышқа қалып қалады).
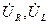 және
және 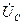 векторлардың геометрикалық қосындысы тізбекке ынта салынған кернеудің векторын береді:
векторлардың геометрикалық қосындысы тізбекке ынта салынған кернеудің векторын береді:
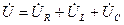
Катеттері 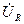 және
және 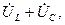 гипотенузасы
гипотенузасы 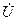 -ға тең тұра бұрышты – кернеулер ұшбұрышы деп аталады.
-ға тең тұра бұрышты – кернеулер ұшбұрышы деп аталады.
б) 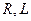 және
және 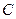 -нің параллельді қосылуы.
-нің параллельді қосылуы.
Кирхгофтың бірінші заңына сәйкесті комплексті әсерлік мәндер үшін жазамыз:
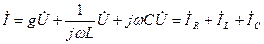 (3.18)
(3.18)
мұнда 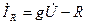 кедергідегі тоқ (
кедергідегі тоқ ( 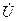 кернеумен фаза бойынша біртектес);
кернеумен фаза бойынша біртектес);
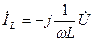 -индуктивтіктегі тоқ (кернеуден 90° қалады);
-индуктивтіктегі тоқ (кернеуден 90° қалады);
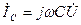 -сыйымдылықтағы тоқ (кернуден 90° озады).
-сыйымдылықтағы тоқ (кернуден 90° озады).
Көрініс
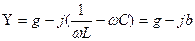 (3.19)
(3.19)
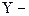 қаралып жатқан тізбектің комплексті өткізгіштігі;
қаралып жатқан тізбектің комплексті өткізгіштігі;
