Симметриялық құраушылар әдісі 4 страница

8.4 Синусоидалсыз периодикалы қисықтардың түрін сипаттайтын коэффициенттер

Синусоидалсыз периодикалы қисықтарды бағалаған кезде электр энергетикада 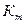қисық түрінің коэффициентімен, 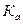амплитуданың коэффенцитімен және 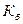бұрмалау коэффициентімен пайдаланады.

а) түрінің коэффициенті әрекет мәнінің орташа мәніне қатынасы деп белгіленеді:

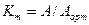(8.11)

синусоида үшін ;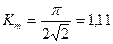

б) амплитуданың коэффициенті-максималды мінінің әрекет мәніне қатынасы деп белогілінеді:

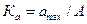
синусоида үшін 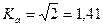; (8.12)

в) бұрмалану коэффициенті –негізгі гармониканың әрекет мәнінің барлық қисықтың әрекет мәніне қатынасы деп белгіленеді:

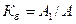(8.13)

синусоида үшін .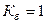

8.5 Синусоидалсыз периодикалы ЭҚК-тер, кернеулер және токтар бар тізбектерді есептеу

Егер де тізбекте бір немесе бірнеше синусоидалсыз периодикалы ЭҚК-тердің көздері болса, онда есептеу үш кезеңге бөлінеді:

а) көздердің ЭҚК-терін тұрақты және синусоидалды құраушыларға жіктеу;

б) тізбектегі токтарды және кернеулерді әрбір құраушы үшін бөлек есептеу;

в) беттесу принципін қолданып әрбір құраушы үшін табылған шешімді бірлесіп қарау.

Егер де ЭҚК (8.6,а –сурет) тең 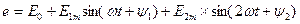онда мұнда ЭҚК-тердің көзінің әрекеті үш тізбекті қосылған ЭҚК-тердің әрекетіне ұқсас (8.6,б-сурет ).

Мұндағы 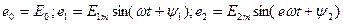(8.14)

а) б)

8.6-сурет

Әрбір ЭҚК-тің әрекетін бөлек қарап, ал содан кейін беттесу принципті қолданып тізбектің барлық бөліктеріндегі токтардың құраушыларын табамыз.

Тізбектегі токтың лезді мәні құрастырушы токтардың лезді мәндерінің қосындысына тең, яғни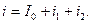

Сонымен синусоидалсыз ЭҚК-тері бар сызықты тізбектерді есептеу синусоидалды ЭҚК-тері бар 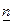есептерді шешуге келтіреді, мұндағы 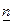-әртүрлі жиіліктері бар ЭҚК-тердің синусоидалды құрастырушылардың саны және тұрақты ЭҚК-і бар бір есеп.

Шешу кезде, әртүрлі жиілік үшін, индуктивтік және сыйымдылық кедергілері бірдей емес екенін еске алу керек. 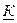-гармоника үшін индуктивтік кедергі бірінші гармоникаға қарағанда 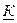есе үлкен , ал сыйымдылық кедергі- 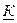есе кіші:

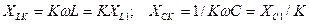(8.15)

Активтік кедергі тұрақты ток кезіндегіге тең. Әрбір гармониканы есептеген кезде комплекстерді қолдануға болады және әрбір гармоника үшін векторлық диаграммаларды салуға болады.

8.6 Синусоидалсыз ток тізбегіндегі қуаттар

Синусоидалсыз периодикалы токтың активтік қуат-период бойынша орта қуат деп белгіленеді

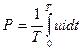(8.16)

Егер де кернеудің және токтың лезді мәндерін тригонометриялық қатар түрінде білдірсек, онда табамыз

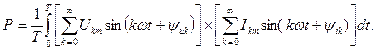
Период ішіндегі әртүрлі жіліктері бар синусоидалардың лезді мәндерінің көбейтулері нөлге тең болғандықтан, шығады

.

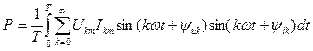Интегралдаудан кейін табамыз

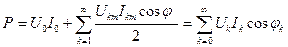, (8.17)

мұндағы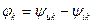

Синусоидалсыз токтың орташа активтік қуаты бөлек гармоникалардың орташа қуаттардың қосындысына тең (тұрақты құраушысы 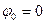тең нөлдік гармоника ретінде қаралады):

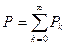. (8.18)

Сикусоидалсыз токтың реактивтік қуаты бөлек гармоникалардың реактивтік қуаттарының қосындысына тең:

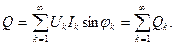(8.19)

Синусоидалсыз токтың толық қуаты токтың және кернеудің әрекет мәндерінің көбейтіндісі ретінде табылады:

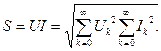(8.20)

Синусоидалсыз токтар кезде қуат коэффициент активтік қуаттың толық қуат қатынасына тең

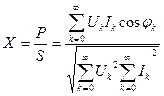(8.21)

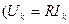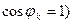(8.21) қатынас тек u және i арасында тұра пропорционал болғанда бірге тең, яғни тізбектің кедергісі таза активтік кезде және . Бір қисықта (кернеуде немесе токта) екінші қисықта жоқ гармониканың болуы активтік және реактивтік қуаттардың шамаларына әсер етпейді, бірақ бұл гармоникалардың құрамында сақтайтын функцияның әрекет мәнін өсіреді. Сондықтан, егер де қаралып жатқан тізбектегі толық қуатты кернеудің және токтың әрекет мәндерінің көбейтіндісі, яғни S=UI деп белгіленген, онда синусоидалды ережеден айрықша синусоидалсыз тізбекте активтік және реактивтік қуаттардың шаршыларының қосындылары қуаттың шаршысына тең емес: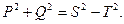

Т шама бұрмалау қуат деп аталады.

Егер де тізбектің кедергісі активтік болса, онда токтың және кернеудің қисықтары түрлес. Бұл жағдайда Q=0 және Т=0.

8.7 Үш фазалы тізбектерде қалыптасқан ереже

Үш фазалы тізбектерде қалыптасқан ереже кезінде екінші және үшінші фазалардағы токтың және кереудің қисықтары бірінші фазадағы үштен бір периодқа ығысқан токтың және кернеудің қисығына түрлес. Егер де А фазадағы кернеу 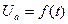уақыт функциямен көрсетілсе, онда 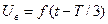және 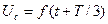, мұндағы Т-негізгі жиіліктің периоды.

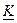ретті гармониканың 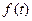функцияны барлық үш фазада қарайық 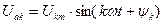болсын.

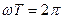тең екенін еске алып және t орнына сәйкесті 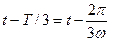және 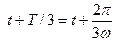қойып, табамыз:

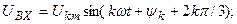
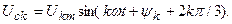
Гармоникалардың реті үшке еселі (k=3n, мұнда n-бүтін сан) кернеулердің барлық фазаларда кез келген уақытта шамалары және бағыттары бірдей.

K=3n+1 кезде үш фазаның гармоникалары симметриялы кернеу жүйені құрады. Жүйенің реттілігі бірінші гармониканың реттелігімен дәл түседі.

K=3n+2 кезде үш фазаның гармоникалары симметриялы кернеу жүйені құрады. Жүйенің реттелігі бірінші гармониканың кері реттілігімен дәл түседі.

Сонымен 1,4,7,10,13 және т.б.реті бар гармоникалар тура реттілігі бар кернеу жүйесін, 2,5,8,11,14 және т.б. реті бар гармоникалар кері реттілігі бар кернеу жүйесін құрса, ал 3,6,9,12 және т.б. реті бар гармоникалар нөлдік реттілігі бар кернеу жүйесін құрады.

Егер де әрбір фазаның кернеуінде тұрақты құраушысы болса, онда ол нөлдік реті бар гармоника деп қаралады, яғни нөлдік реттілікті құрады.

Көпшілік жағдайда кернеулерде тұрақты құраушы және жұп гармоникалар жоқ болады.

Үш фазалық тізбектердің әртүрлі сүлбелерін қарайық.

Егер де генератордың фазалары жұлдызша қосылған болса, онда фазалы синусоидалсыз кернеулер реті үшке еселі кернеулердің гармоникалары құрамында жоқ, себебі олар нөлдік реттіліктегі жүйені құрады.

Фазалық кернеу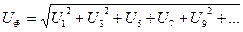

Сызықты кернеу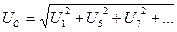

Бұдан шығады .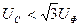

Симметриялы жүктеме кезде негізгі жиіліктің және жоғары гармоникалар реті үшке еселі жоғары гармоникаларды қоспағанда, тура және кері реттелігі бар жүйелерді құрады да қосындылары нөлді береді. Ал реті үшке еселі гармоникалар нөлдік реттелігі бар жүйені құрады, яғни кез келген уақытта олардың мәндері және бағыттары бірдей болады. Сондықтан, нөлдік сымдағы ток нөлдік реттелігі бар жоғары гармоникалардың қосындысының үш есесіне тең: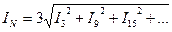

Бейтарап сым жоқ кезде әрбір фазадағы токтың құрамында реті үшке еселі жоғары гармоникалар жоқ. Сондықтан, қабылдағышта нөлдік реттелігі бар токтардан кернеулер жоқ.

Егер де генератордың фазалары үшбұрышқа қосылса, онда фазадағы ЭҚК-тер синусоидалсыз болғанда генератордың тұйықталған контурында әрекет етуші ЭҚК-тердің қосындысы нөлге тең емес, ол реті үшке еселі жоғары гармоникалардың қосындысының үш есесіне тең:

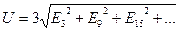
Егер де фазалар тұйықталған үшбұрышқа қосылса, онда реті үшке еселі ЭҚК-тердің гармоникалар генератордың ішкі тоғын туғызады

Генератордың фазалық тоғы

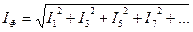
Сыртқы тізбектегі сызықтық ток

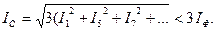
Оныншы тарау

10 Өтпелі процестерді операторлық әдіспен есептеу

10.1 Лапластың түрлендіруін өтпелі процестерді есептеуге қолдану

Өтпелі процестерді классикалық әдіспен есептеу басты жағдай бойынша интегралдаудың тұрақтыларын белгілеу және басты функцияларды және олардың туындыларын табу үшін алгебралық теңдеулердің жүйесін дүркін-дүркін шешуді талап етеді. Бұл жағдай осы әдіспен есептеудің негізгі қиыншылығына жатады. Электр сүлбелер құрделендірген сайын және дифференциялды теңдеудің дәрежесі өскен сайын бұл қиыншылықтарда өседі.

Сондықтан, тапсырылған басты жағдайлар бастапқы теңдеулерге кіргізіліп сызықты дифференциалды теңдеулерді шешу әдісті пайдалану қолайлы болады, өйткені бұл әдісте керекті функцияларды табу үшін интегралдаудың тұрақтыларын белгілеудің қажеттігі жоқ болады.

Сызықты дифференциалды теңдеулерді Лапластың түрлендірулерге негізделген операторлық әдіспен интегралдауға болады.

Операторлық әдістің маңызы – тұп нұсқа деп аталатын кейбір тапсырылған бір қатарлы шектелген заттың айнымалының 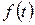функциясына басқа бейнесі деп аталатын 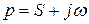комплексті айнымалының 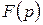функциясы салыстырылады. Функция 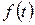әрбір ақырғы уақыт аралықта Дирихле жағдайына қамтамасыз ету керек және 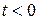кезде нөлге тең болу керек.

Салыстыру мына формула бойынша өткізіледі

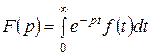(10.1)

(10.1) кейіптеме - 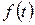функцияның үстінен Лапластың тікелей түрлендіруін көрсетеді.

Оны былай белгілейді:

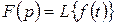немесе 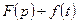, мұнда 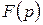- 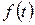функцияның Лапластық бейнесі. Кері, егерде 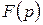бейнесі бойынша 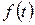түп нұсқаны табу керек болса, онда Лапластың кері түрлендіруі қолданады

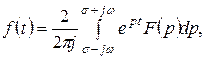(10.2)

яғни (10.1) интегралды теңдеуді 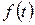функцияға қатысты шешу.

(10.2) интегралды былай белгілеугенде болады:

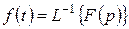немесе .

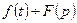Тұп нұсқадан туындылардың және интегралдардың бейнелері үшін кейіптемелерін (шығарусыз) келтірейік:

Егер де 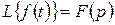болса, онда (10.3)

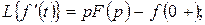(10.4)

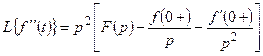және т.с.с. (10.5)

Егер де 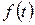функция және оның туындылары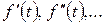 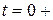кезде кенет өзгерсе, онда (9.4) және (9.5) кейітемелерге олардың мәнін осы кенет өзгерісті есепке алып қою керек яғни нөлдің оң жағында, бұл жағдай олардың аргументтерінде 0+ белгімен көрсетілген. Егер де 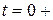кезде функцияның және оның туындыларының басты мәндері нөлге тең болса, онда бірінші және одан соңғы туындылардың бейнелері өте жеңіл табылады:

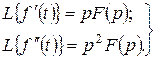және т.с.с. (10.6)

Тұп нұсқаудың интегралдық бейнелерінің түрі:

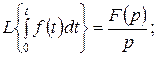(10.7)

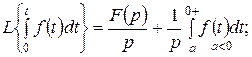(10.8)

Егерде интеграл 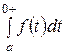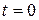кезде кенет өзгерсе, онда оның мәнін нөлдік оң жағынан алу керек, бұл жағдай оның жоғары шегінде 0+ белгімен көрсетіледі.

10.2 Жіктеудің теоремасы

Бейне 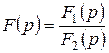(10.9) дұрыс бөлшек түрде берілсін, алымның және бөлгіштің жалпы түбірлері жоқ. 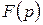функцияның полюстерінің орыны 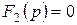(10.10) теңдеудің түбірлерімен белгіленеді. (10.10) теңдеудің 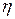түбірлерін 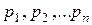деп белгілейміз.

Екі жағдай болуға мүмкін: а) барлық түбірлер жай; б) кейбір немесе барлық түбірлер еселі.

а) жай түбірлердің жағдайы

Өте жай жағдайда бейне радионалды бөлшек түрде болады:

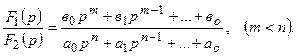(10.11)

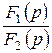бөлшек қысқарылмайды, яғни 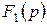және 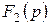мүшелердің жалпы түбірлері жоқ, ал 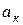және 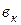- заттық сандар. (10.11) бейненің түп нұсқасын жікте теормасы деп аталатын кейіптеме бойынша табуға болады:

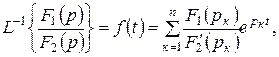(10.12)

Мұнда p_к сипаттамалы теңдеудің, яғни 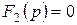теңдеудің жай түбірлері, бір түбір нөлге тең болуы мүмкін.

Егер де бір түбір нөлге тең болса, яғни бөлгіш ішінде (10.11) р көбейткіш бар болса, онда жіктеу теореманың басқа түрі қолданады.

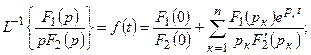(10.13)

б) еселі түбірлердің жағдайы

Егер де көп мүшелі 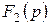түбірлерінің ішінде еселі түбірлер болса, онда жіктеу теореманы (10.12) және (10.13) формулаға ұқсасты жасауға болады, бірақ оң жағында қосындымен (бір қосынды түбірлер саны бойынша, ал екінші әрбір түбір үшін оның еселік реттігімен).

Сонымен, 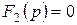теңдеуде еселі түбірлер болса, онда 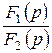кесінді бойынша тұп нұсқау мына формула бойынша есептеледі:

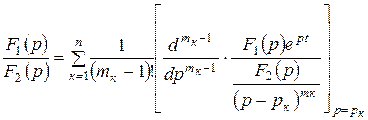(10.14)

Шаршы жақшаның бөлгішіндегі көріністі алдымен 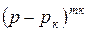шамаға қысқартып, содан кейін дифференциялдау керек.

Егер де 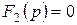теңдеуде бір мезгілде жай және еселі түбірлер болса, онда жай түбірлерге сәйкесті қосындыларды (10.12) және (10.13) формулалар, ал еселі түбірлер үшін - (10.14) формула қолданады.

10.3 Операторлық түрдегі Ом және Кирхгофтың заңдары

10.1 – суреттегі R, L, C тізбек 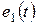ЭҚК-ке қосылып тұрған, ал 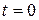ұақыт мезгілде 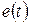ЭҚК-ке ауысып қосылады.

Ауысып қосылғаннан кейін Кирхгофтың екінші заңы лезді мәндер үшін былай жазылады.

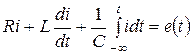(10.15)

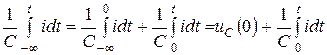. (10.16)

мұнда 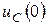- сыйымдылықта ауысып қосу кездегі кернеу, яғни 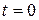кезде.

Лезді мәндер үшін жазылған тұп нұсқауынан оның операторлық түрде жазылған бейнесіне өту үшін (10.1) кейіптемеге сәйкес былай істеледі: (10.15) теңдіктің екі жағын 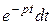шамаға көбейтіп нөлден шексіздікке дейін интегралдау керек. Онда шығады:

.

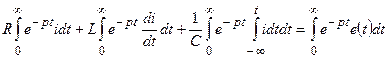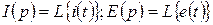деп есептеп және (10.4), (10.7), (10.16) кейіптенелерді есепке алып, шығарамыз:

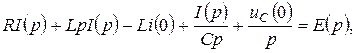ал бұл теңдеуден R, L, C тізбек үшін операторлық түрде Омның заңы шығады

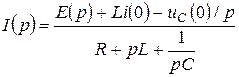(10.17)

Бөлгіште тұрған көрініс операторлық кедергі деп аталады 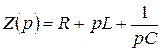. (10.18)

Операторлық кедергіге кері шама операторлық өткізгіш деп аталады 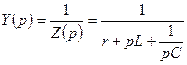. (10.19)

Басты жағдайлар нөлге тең болса, яғни 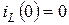және 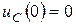болса, онда (10.17) көрініс:

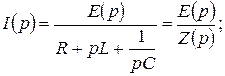(10.20)

яғни комплексті түрдегі Ом заңына толық ұқсас.

Тармақталған тізбектін әрбір түйіні үшін

.

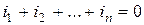Сондықтан токтың кесіндісін 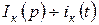белгілеп Кирхгофтың бірінші заңын операторлық түрде жазамыз:

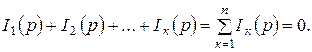(10.21)

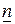тармақтан құралған әрбір тұйықталған контур үшін

.

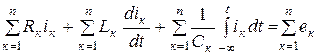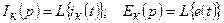деп есептеп Кирхгофтың екінші заңы операторлық түрде жазылады:

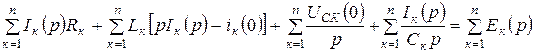, ал бұны былай жазуға болады:

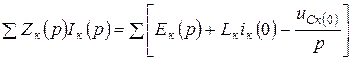(10.22)

Былай жазылған түрд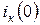е және 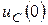- индуктивтік орауыштардағы токтың және конденсаторларды кернеудің басты мәндері.

Егер де басты жағдайлар нөлге тең болса, онда Кирхгофтың екінші заңы былай жазылады:

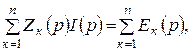(10.23) яғни бұл жағдайда ол Кирхгофтың екінші заңы комплексті түрде жазылғанға толық ұқсас.

Сонымен Омның және Кирхгофтың заңдары операторлық түрде өздерінің жазылу түрі бойынша синусоидалды ток тізбегі үшін сол заңдардың комплексті түрде жазылғанға ұқсас.