Симметриялық құраушылар әдісі 5 страница
Бірақ есте ұстау керек, бірінші – басты жағдайлар нөлге тең болмағанда, яғни 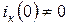 және
және 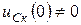 болғанда әрбір к тармақта сыртқы ЭҚК
болғанда әрбір к тармақта сыртқы ЭҚК 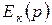 -дан басқа ішкі ЭҚК-тер
-дан басқа ішкі ЭҚК-тер 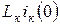 және
және 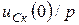 әсер етеді (олардың болымды бағыттары сол тармақтағы токтың болымды бағытына сәйкес), екінші – тармақтың кедергісі ретінде операторлық кедергі алынады.
әсер етеді (олардың болымды бағыттары сол тармақтағы токтың болымды бағытына сәйкес), екінші – тармақтың кедергісі ретінде операторлық кедергі алынады.
10.4 Баламалы операторлық сүлбелер
Операторлық әдіспен өтпелі процесті есептеген кезде берілген тізбек үшін баламалы операторлық сүлбені құру пайдалы болады.
Басты жағдайлар нөлге тең болмағанда баламалы операторлық сұлбаны құруды 10.2-суретте келтірілген сүлбені қарайық.
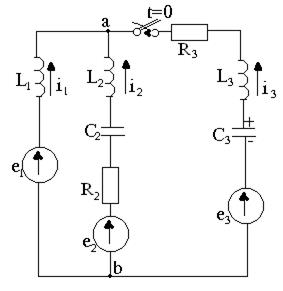
10.2 – сурет. Тізбектің электр сұлбасы
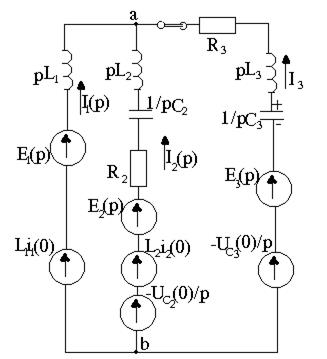
10.3 – сурет. Тізбектің баламалы операторлық сұлбасы
Кирхгофтың заңдарын операторлық түрде жазамыз:
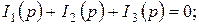
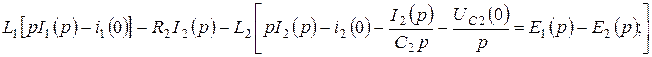
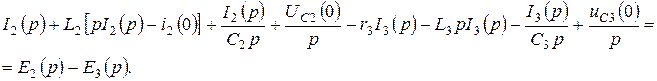 Қайтадан мына түрде жазамыз:
Қайтадан мына түрде жазамыз:
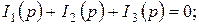
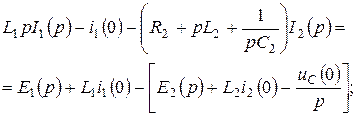
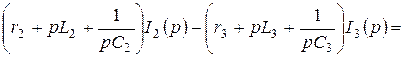
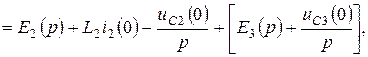 бұл теңдеулер бойынша 10.3 – суретте келтірілген балама операторлық сүлбені құрамыз.
бұл теңдеулер бойынша 10.3 – суретте келтірілген балама операторлық сүлбені құрамыз.
Тізбектерді есептеу әдістердің токпен кернеудің кесінділерін есептеу үшін (10.3-сурет) контурлық тоқ, түйінді потенциалдар ж.т.б. әдістерді қолдануға болады.
10.5 Пассивтік екіұштықты ұздіксіз өзгеріп тұрған кернеу көзіне қосу (Дюамельдін интегралы)
Мейлі еркінше пассивтік сызықты екіұштық 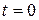 ұақыттан бастап үздіксіз өзгеріп тұрған кернеу көзіне қосылсын (10.4 – сурет). Екі ұштықтың қандайда болған тармағында кілт тұйықталғанда ток
ұақыттан бастап үздіксіз өзгеріп тұрған кернеу көзіне қосылсын (10.4 – сурет). Екі ұштықтың қандайда болған тармағында кілт тұйықталғанда ток 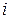 -ді (немесе
-ді (немесе 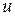 -ды) табу керек.
-ды) табу керек.
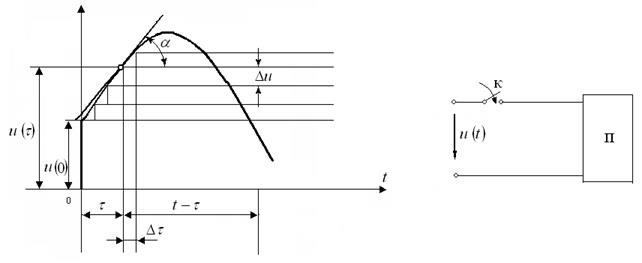
10.4 – сурет
Есепті екі кезеңге бөлеміз. Алдымен керекті шаманы екіұштықты жекелеген кернеудің ырғағына қосқан кезде табамыз (кернеу тұрақты және сан бойынша бірге тең).
Жекелеген ырғақ (жекелеген сатылы әсер ету) жекелеген сатылы функциямен беріледі –10.5-суреттегі бейнеленген 1(t) Хевисайдтың функциясымен.
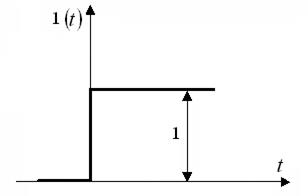
10.5 – сурет
Электр тізбектер теориясының көзғарасы бойынша тізбектің кірісінде әрекет істейтін жекелеген тұрақты кернеу (немесе ток) 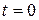 + уақыт кезінде.
+ уақыт кезінде.
Сонымен 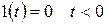 кезінде;
кезінде;
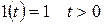 кезінде. (10.24)
кезінде. (10.24)
Жекелеген ырғақ әсер еткендегі сан бойынша ізделіп отырған токқа (немесе кернеуге) тең 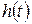 функция өтпелі функция деп аталады. Бұл тізбектің жекелеген ырғаққа әсерлістігі.
функция өтпелі функция деп аталады. Бұл тізбектің жекелеген ырғаққа әсерлістігі.
Мысалы, R, L – тізбек үшін кернеудің өтпелі функциясы 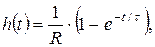 ал RC-тізбек үшін кернеудің өтпелі функциясы
ал RC-тізбек үшін кернеудің өтпелі функциясы 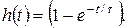
Өтпелі функцияны, қандайда болған екіұштықтық сүлбесі болғанда, классикалық немесе операторлық әдіспен табуға болады. Сонымен, есептеу кезде 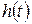 функция белгілі деп санаймыз.
функция белгілі деп санаймыз.
Пассивтік екіұштық қосылып тұрғандықтан 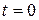 кезде токтар және кернеулер тармақтарда нөлге тең, яғни t<0 кезде
кезде токтар және кернеулер тармақтарда нөлге тең, яғни t<0 кезде 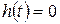 .
.
Тоқты есептеу жағдайын қарап шығайық.
Үздіксіз өзгеріп тұрған 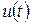 кернеуді
кернеуді 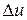 тура бұрышты ырғақтары бар сатылы функциямен алмастырамыз (10.6 – сурет).
тура бұрышты ырғақтары бар сатылы функциямен алмастырамыз (10.6 – сурет).
Онда кернеу өзгерудің процесін 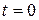 кезде
кезде 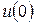 тұрақты кернеуді қосу деп, ал содан кейін бірбірінен
тұрақты кернеуді қосу деп, ал содан кейін бірбірінен 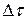 уақыт аралыққа ығысқан
уақыт аралыққа ығысқан 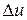 элементарлы тұрақты кернеулердің қосылуы деп көрсетуге болады. Кернеудің қисығына өскенде + таңба, ал төмендегенде – таңба қойылады.
элементарлы тұрақты кернеулердің қосылуы деп көрсетуге болады. Кернеудің қисығына өскенде + таңба, ал төмендегенде – таңба қойылады.
Ізделіп жатқан тоқтың 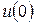 тұрақты кернеуден t уақыт кездегі құрастырушысы
тұрақты кернеуден t уақыт кездегі құрастырушысы 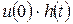 тең. Тоқтың құрастырушысы t уақыт кезде
тең. Тоқтың құрастырушысы t уақыт кезде 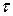 уақыт кезде қосылатын
уақыт кезде қосылатын 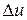 ырғақты кернеуден тең
ырғақты кернеуден тең 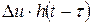 . Мұнда өтпелі функцияның аргументі ретінде уақыт
. Мұнда өтпелі функцияның аргументі ретінде уақыт 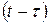 алынады. Оған себеп болатыны -
алынады. Оған себеп болатыны - 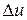 кернеудің ырғағының әрекеті кілт тұйықталғаннан кейін
кернеудің ырғағының әрекеті кілт тұйықталғаннан кейін 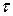 уақыт өткенде басталады.
уақыт өткенде басталады.
Кернеудің элементарлы ырғағы
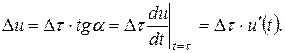
Сондықтан токтың ізделіп жатқан құрастырушысы
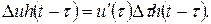 (10.25)
(10.25)
Кернеудің элементарлы ырғақтары 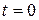 -ден t кездегі уақыт аралықта қосылады. Сондықтан, барлық ырғақтардан токтың құрастырушыларын жинақтап,
-ден t кездегі уақыт аралықта қосылады. Сондықтан, барлық ырғақтардан токтың құрастырушыларын жинақтап, 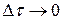 кезде шекке өтіп және
кезде шекке өтіп және 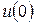 басты кернеудің ырғағынан токтың құрастырушысын есепке алып табамыз.
басты кернеудің ырғағынан токтың құрастырушысын есепке алып табамыз.
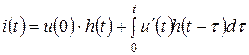 (10.26)
(10.26)
(10.26) кейіптеме Дюамельдің интегралы деп аталады.
10.6 Пассивтік екіұштықты еркінше түрі бар кернеу көзіне қосу
Кернеудің еркінше түрі-кесекті-аналитикалық функциясымен белгіленетін кернеудін өзгеруін айтады.
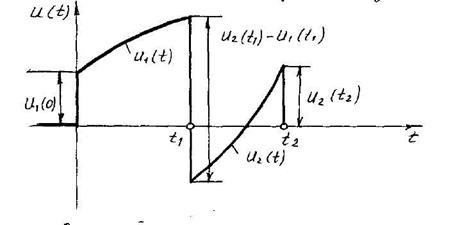
10.6 – сурет
Пассивтік екіұштық, өзгеру қисығы 10.6 – суретте берілген, кернеу көзіне қосылады.
Токты белгілеу үшін жоғарыдай h(t) – өтпелі функцияны белгілейміз.
Қосылатын кернеу 0<t<t1 аралықта 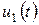 функциямен берілген болғандықтан (10.26) кейтемені пайдаланып бұл уақыт аралыққа жазуға болады
функциямен берілген болғандықтан (10.26) кейтемені пайдаланып бұл уақыт аралыққа жазуға болады
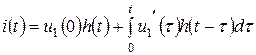 . (10.27)
. (10.27)
Келесі уақыт аралықта (t1<t<t2) кернеу басқа 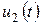 функциямен беріледі. Бұл кернеу t1 мезгілде
функциямен беріледі. Бұл кернеу t1 мезгілде 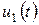 мәнінен
мәнінен 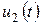 мәніне дейін ырғақты өзгереді. Кернеудің ырғағын есепке алу үшін t=t1 нүктеде екіұштыққа кері тұрақты кернеу
мәніне дейін ырғақты өзгереді. Кернеудің ырғағын есепке алу үшін t=t1 нүктеде екіұштыққа кері тұрақты кернеу 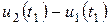 бұл мезгілде ынта салынып тұр деп санайық. Онан басқа, кернеудің бастапқы ырғағынан
бұл мезгілде ынта салынып тұр деп санайық. Онан басқа, кернеудің бастапқы ырғағынан 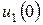 және кернеудің элементарлы ырғақтарынан токтардың құрастырушыларын есепке алып, нәтижесінде табамыз
және кернеудің элементарлы ырғақтарынан токтардың құрастырушыларын есепке алып, нәтижесінде табамыз
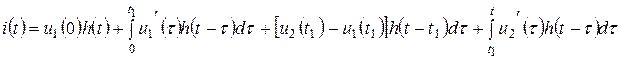
(10.28)
Аяғында, t2<t< 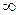 уақыт аралық үшін t=t2 мезгілде -
уақыт аралық үшін t=t2 мезгілде - 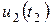 тұрақты кернеу қосылғанды және
тұрақты кернеу қосылғанды және 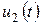 кернеу қисығымен белгіленетін элементарлы ырғақтар t=t2 уақыт мезгілге дейін әрекет ететінін есепке алып, табамыз
кернеу қисығымен белгіленетін элементарлы ырғақтар t=t2 уақыт мезгілге дейін әрекет ететінін есепке алып, табамыз
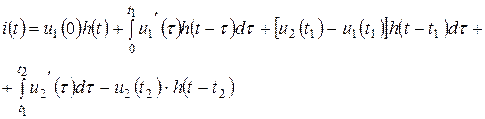 (10.29)
(10.29)
Онбірінші тарау
11 Төртұштықтар
11.1 Негізгі анықтамалары және топтастыру
Екі жұп шықпаларға қарай қарылып тұрған электр тізбектің бөлігі төртұштық деп аталады. «Төртұштық» деген ұғыммен электр тізбектің екі тармақталарындағы тоқтармен және кернеулермен қызыққан кезде пайдаланады.

11.1 – сурет. Төртұштық
Төртұштық ретінде электр генератор және электр қозғалтқыш, трансформатор, электр сүзгіш, күшейткіш, электр желілер және көзбен қабылдағыштың арасында қосылған екі жұп шықпалары бар басқа құрылғылар жатады.
Төртұштықтың электр энергияның көзі қосылған шықпалар кіріс деп аталады, жүктеме қосылған шықпалар – шығыс деп аталады.
Төртұштықтар топтастырылады:
1. Олардың ішінде кіретін элементтердің нышаны бойынша;
2. Ішкі құрамасының сүлбесі бойынша – Г – түрлі (10.2,а – сурет), Т – сияқты (10.2,б – сурет), П – сияқты (10.2,в – сурет) көпірлі (10.2,г – сурет).
Активтік төртұштықтар ішінде энергия көздері бар, ал егерде энергия көздері жоқ болса немесе олар өзара компенсацияланса, онда төртұштық пассивтік болады.
Егер де төртұштықтың ішіндегі көздердің әрекеттері өзара бір – бірін компенсацияланса, онда төртұштықтың автономды деп аталады.
Егер де төртұштықтың ішіндегі көздер тәуелді болса (мысалы, транзисторлар), онда төртұштықтың тізбектің басқа жағынан ажыратылған кезде ажыратылған шықпаларда кернеу жоқ болады. Мұндай төртұштықтың
автономды емес деп аталады. Егер де кіріс және шығыс шықпаларды ауыстырған кезде тоқтармен кернеулер өзгермесе төртұштықтық симметриялы. Басқа жағдайда төртұштықтың симметриясыз.
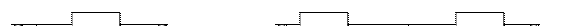
11.2– сурет. Төртұштықтардың түрлері.
Төртұштық қайтымды, егер де шығыстағы тоқтың кірістегі кернеуге қатынасы қайсы екі жұп шықпалар кіріс, ал қайсы шығыс болғанда тәуелді болмаса.
Пассивтік симметриялы төртұштықтың – қайтымды, ал симметриясыз – қайтымды емес.
Кіріс және шығыс шықпалары бар күрделі электр тізбек белгілі сүлбе бойынша қосылған құрама төртұштықтардың жиынтығы болып қаралады.
Төртұштықтың теориясы мұндай күрделі төртұштықтың параметрларын құрама төртұштықтардың параметрлары арқылы есептеуге рұқсат береді және күрделі төртұштықтың тоқтарымен кернеулердің арасындағы тәуелділікті, берілген сүлбенің ішіндегі тоқтарды және кернеуді есептемей, табуға жағдай туғызады.
11.2 Төртұштықтардың теңдеулер жүйелері
Тәуелсіз электр энергияның көздері жоқ төртұштықтың жұмыс ережесін қарап шығайық.
Біріншілік және екіншілік шықпалардағы ережені белгілейтін екі тоқтың және екі кернеудің арасындағы тәуелділіктер әртүрлі түрде жазылуы мүмкін. Егер де көрсетілген екі шама берілген болса, онда басқа екі шама олармен екі тендеулер жүйемен байланысады. Бұл теңдеулер төртұштықтың теңдеулері деп аталады.
Түрі бойынша әртүрлі, бірақ негізінде эквивалентті алты теңдеулер жүелерді жазып алуға болады.
1. А түрлі теңдеулер:
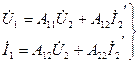 (11.1)
(11.1)
Бұл теңдеуде 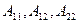 және
және 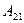 коэффициенттер төртұштықтың өзін белгілейді. Олар қосылу сүлбесінен және төртұштықты құрайтын электр тізбектің элементтерінен тәуелді.
коэффициенттер төртұштықтың өзін белгілейді. Олар қосылу сүлбесінен және төртұштықты құрайтын электр тізбектің элементтерінен тәуелді. 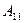 және
және 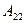 өлшемі жоқ коэффициенттер,
өлшемі жоқ коэффициенттер, 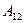 кедергінің өлшемі,
кедергінің өлшемі, 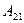 өткізгіштің өлшемі.
өткізгіштің өлшемі.
2. Y түрлі теңдеулер:
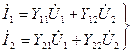 (коэффициенттер - өткізгіштік) (11.2)
(коэффициенттер - өткізгіштік) (11.2)
3. Z түрлі теңдеулер:
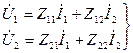 (коэффициенттер – кедергілер) (11.3)
(коэффициенттер – кедергілер) (11.3)
4. Н түрлі теңдеулер:
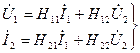 (11.4)
(11.4)
5. G түрлі теңдеулер:
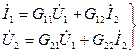 (11.5)
(11.5)
6. В түрлі теңдеулер:
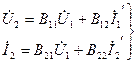 (11.6)
(11.6)
11.3 Төртұштықтардың ережелері
Тоқтардың болымды бағыттарын (11.3,а – сурет) көріктендіру көздер біріншілік (кіріс) шықпаларда және 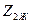 кедергісі бар қабылдағыш екіншілік (шығыс) шықпаларында болған төртұштық үшін көрсетілген сияқты, ал теңдеулер А түрде жазылады.
кедергісі бар қабылдағыш екіншілік (шығыс) шықпаларында болған төртұштық үшін көрсетілген сияқты, ал теңдеулер А түрде жазылады.
Кері болымды бағыттар – көріктендіру көздер екіншілік шықпаларында және 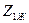 кедергісі бар қабылдағыш біріншілік шықпаларда (11.3,б – сурет) көрсетілген. Теңдеулер В түрде жазылады.
кедергісі бар қабылдағыш біріншілік шықпаларда (11.3,б – сурет) көрсетілген. Теңдеулер В түрде жазылады.

Кіріс кедергілер. 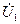 кернеудің
кернеудің 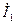 тоққа қатынасы (11.3,а – сурет)
тоққа қатынасы (11.3,а – сурет) 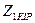 кіріс кедергі біріншілік шықпалар жақтан деп аталады, ал
кіріс кедергі біріншілік шықпалар жақтан деп аталады, ал 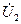 кернеудің
кернеудің 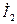 тоққа қатынасы (11.3,б – сурет)
тоққа қатынасы (11.3,б – сурет) 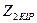 кедергі екіншілік шықпалар жақтан деп аталады.
кедергі екіншілік шықпалар жақтан деп аталады.
11.3 – сурет
Кіріс кедергі көріктендіру көздің жұмыс ережесін белгілейді. Ол төртұштықты құрайтын элементтердің қосындысына және параметрлеріне, яғни төртұштықтың коэффициенттеріне тәуелді және жүктеменің кедергісіне тәуелді.
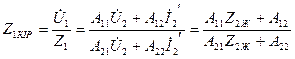 (11.7,а)
(11.7,а)
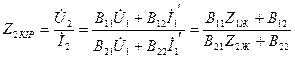 (11.7,б)
(11.7,б)

11.4 – сурет
Біріншілік шықпалардан көріктендірілген кезде, ал екіншілік шықпалар қысқа тұйықталған кезде, яғни 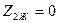 болғанда (11.4,а – сурет), кіріс кедергі:
болғанда (11.4,а – сурет), кіріс кедергі:
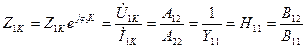 (11.8)
(11.8)

11.5 – сурет
Екіншілік шықпаларда бос жүріс ереже кезде, яғни 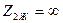 болғанда (11.5,а – сурет) кіріс кедергі:
болғанда (11.5,а – сурет) кіріс кедергі:
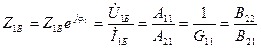 (11.9)
(11.9)
Екіншілік шықпалардан көріктендірілген кезде, ал біріншілік шықпалар қысқа тұйықталғанда, яғни 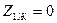 болғанда (11.4,б – сурет) кіріс кедергі:
болғанда (11.4,б – сурет) кіріс кедергі:
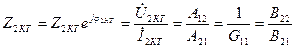 (11.10)
(11.10)
Біріншілік шықпалар бос жүріс ереже кезде, яғни 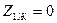 болғанда (11.5,б – сурет) кіріс кезінде:
болғанда (11.5,б – сурет) кіріс кезінде:
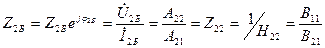 (11.11)
(11.11)
Қысқа тұйықталудың және бос жүрістің кедергілері ұштықтың коэффициенттерімен белгіленеді:
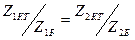 (11.12)
(11.12)
Егер де коэффициенттер белгілі болса, онда төртұштық берілген болады.
Теңдеулердің бір түрлерінің коэффициенттерінің матрицасы басқа теңдеулер түрінің коэффициенттерінің матрицасы арқылы көрсетуге болады.
Төртұштықтың теңдеулер коэффициенттері біріншілік параметрлар деп аталады. Егер де төртұштықтың сүлбесі және оны құрастырушы элементтердің шамалары белгілі болса, онда коэффициенттерді есептеумен белгілеуге болады.
Мысал.11.1: А түрлі теңдеулердің коэффициенттерін табу керек (11.6 – сурет)
Шешу:
 |
Кирхгофтың заңдары көмегімен
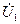 кернеуді және
кернеуді және 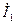 тоқты
тоқты 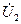 кернеу және
кернеу және 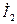 тоқ арқылы білдірейік.
тоқ арқылы білдірейік.
11.6 – сурет
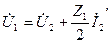
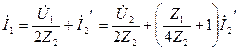
А түрлі теңдеулермен (10.1) бұл тәуелділіктері салыстырып табамыз:
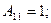
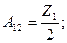
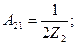
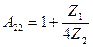
Симметриялы төртұштық
Симметриялы төртұштықтың өзара кіріс және шығыс шықпаларды алмастырған кезде көздің және қабылдағыштың жұмыс ережесі өзгермейді.
Симметриялы төртұштық үшін 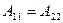
 |
Мысал.11.2: А түрлі теңдеулердің коэффициентерін табу керек (11.7 - сурет)
11.7 – сурет.
Шығыс шықпалар ажырап тұрғанда (бос жүріс ереже) 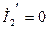 тең
тең
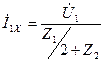 ;
; 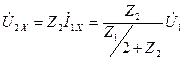
Бұл теңдеулерді (10.1) теңдеулермен ( 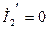 тең кезде) салыстырып
тең кезде) салыстырып
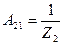 ;
; 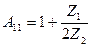
Екінші шықпалар қысқа тұйықталса ( 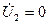 кезде)
кезде) 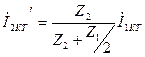 ; немесе
; немесе 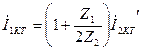 ;
;
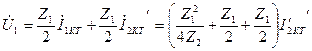
Бұл теңдеулердің (10.1) теңдеулермен ( 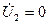 кезде) салыстырып табамыз:
кезде) салыстырып табамыз:
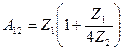 ;
; 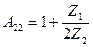 , яғни
, яғни 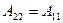
Бұл жағдай симметриялық төртұштықтарда болады.
11.4 Пассивтік төртұштықтардың екіншілік (сипаттамалы) параметрлері
Төртұштықты, оның кіріс кедергісі жүктеу кедергіге тең болу үшін, қалай жүктеу керек?
Көріктендіру көзді біріншілік шықпаларға қосайық (11.8,а – сурет)

11.8 – сурет
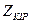 кіріс кедергіні (11.7,а) бойынша, симметриялы төртұштық үшін
кіріс кедергіні (11.7,а) бойынша, симметриялы төртұштық үшін 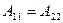 есепке алып, табамыз:
есепке алып, табамыз:
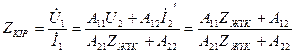 (11.13)
(11.13)
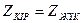 болу керек, яғни
болу керек, яғни
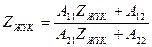 (11.14)
(11.14)
(11.14) өрнек 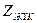 жүктеменің кедергісін
жүктеменің кедергісін 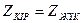 болғанда шамасын белгілейді.
болғанда шамасын белгілейді.
(11.14) теңдеуден шығады
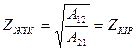 (11.15)
(11.15)
Мұндай жүктеме кезде төртұштықтың кіріс кедергісі оның параметрлерінен ( 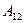 және
және 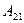 ) тәуелді, ал сондықтан төртұштықтың бір параметрамен алуға болады. Жаңа параметрды білу керек, егер де дайын төртұштыққа
) тәуелді, ал сондықтан төртұштықтың бір параметрамен алуға болады. Жаңа параметрды білу керек, егер де дайын төртұштыққа 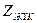 таңдау керек болғанда, немесе, кері, жүктемесі берілген қабылдағышқа төртұштықты жобалау керек. Бұл параметр
таңдау керек болғанда, немесе, кері, жүктемесі берілген қабылдағышқа төртұштықты жобалау керек. Бұл параметр 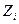 деп белгіленеді, оны төртұштықтық сипаттамалы кедергісі деп атайды
деп белгіленеді, оны төртұштықтық сипаттамалы кедергісі деп атайды
Дата добавления: 2017-01-29; просмотров: 2111;
