Симметриялық құраушылар әдісі 8 страница
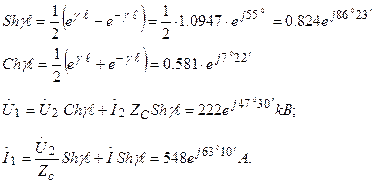
Желің басындағы ток кернеуден 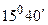 бұрышқа озады.
бұрышқа озады.
3 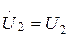 тең болғандықтан желінің басымен аяғындағы кернеулер арасындағы фазалық ығысу
тең болғандықтан желінің басымен аяғындағы кернеулер арасындағы фазалық ығысу 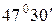 тең.
тең.
4 Желіге берілетін активтік қуат
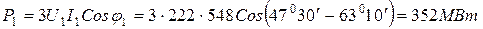
5 Желінің ПӘК-і
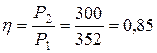 .
.
13.5 Біртекті желінің сипаттамалары
Әлсірету коэффициенті
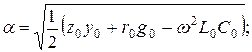 (13.28)
(13.28)
Фазалық коэффициент
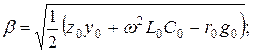 (13.29)
(13.29)
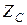 орташа мәні:
орташа мәні:
1. ауа желілер үшін 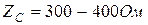 ;
;
2. кабельдер үшін 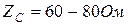 .
.
13.3 – суретте (13.10) және (13.11) бойынша салынған 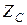 және Ө үшін жиілік сипаттамалар көрсетілген
және Ө үшін жиілік сипаттамалар көрсетілген
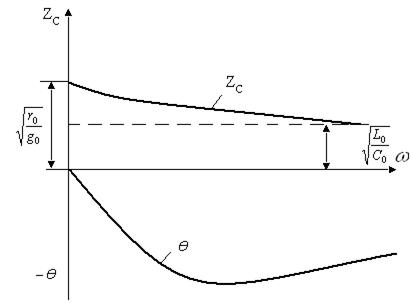
13.3-сурет
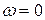 кезінде
кезінде 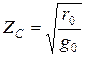 (13.30)
(13.30)
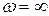 кезінде
кезінде 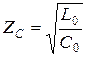 (13.31)
(13.31)
Ө нөлге тең 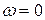 және
және 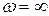 кезінде.
кезінде. 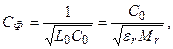 (13.32)
(13.32)
мұндағы 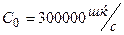 -вакуумдағы жарықтықтың жылдамдығы,
-вакуумдағы жарықтықтың жылдамдығы, 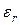 және
және 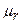 -сымды коршайтын кеңістіктің диэлектрик және магниттік тұрақтылары.
-сымды коршайтын кеңістіктің диэлектрик және магниттік тұрақтылары.
Ауа желілер үшін 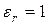 және
және 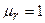 толқындардың жылдамдағы с тең, ал кабельді желілерде толқындардың жылдамдығы С –ден 2-2,5 есе төмен.
толқындардың жылдамдағы с тең, ал кабельді желілерде толқындардың жылдамдығы С –ден 2-2,5 есе төмен.
АЭЖ –лерде 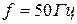 кезінде толқынның ұзындығы
кезінде толқынның ұзындығы
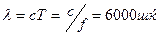
13.6 Желінің кіріс кедергісі және толқынның шағылу коэффициенті
Желінің Zкір кіріс кедергісі ретінде желінің басындағы ережені есептеу кезінде желінің оның аяғында жүктемемен бірге екіұштықтың кедергісімен алмастыруыды ұғады, яғни
 (13.33)
(13.33)
Қандай да болған 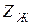 жүктеме кедергісі кезінде кіріс кедергіні бос жүріс кездегі
жүктеме кедергісі кезінде кіріс кедергіні бос жүріс кездегі 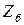 және қысқа жұйықтау кездесі
және қысқа жұйықтау кездесі 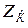 кедергілер арқылы көрсетуге болады
кедергілер арқылы көрсетуге болады
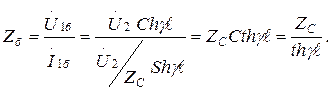 (13.34)
(13.34)
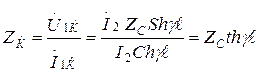 (13.35)
(13.35)
(13.33) теңдеудің оң жағының алымын және бөлгішін 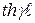 бөліп (13.34) және (13.35) есепке алып, табамыз
бөліп (13.34) және (13.35) есепке алып, табамыз
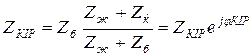 (13.36)
(13.36)
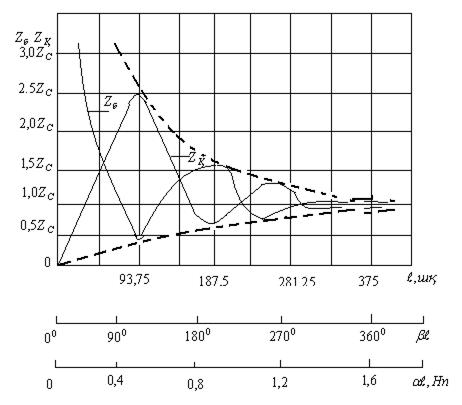
13.4-сурет
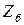 және
және 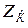 желінің бос жүріс және қысқа тұйықталу тәжірібелер арқылы табылады.
желінің бос жүріс және қысқа тұйықталу тәжірібелер арқылы табылады. 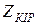 және
және 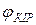 желінің ұзындағы өзгерген кезде толқынды өзгереді (13.4-сурет).
желінің ұзындағы өзгерген кезде толқынды өзгереді (13.4-сурет).
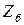 және
және 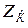 арқылы
арқылы 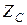 және
және 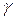 жеңіл табылады.
жеңіл табылады.
(13.34) және (13.35) теңдеулері бір-біріне көбейтіп, содан кейін мүшелер бойынша бөліп және түбір астынан шығарып, табамыз
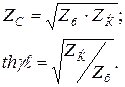
Желінің аяғындағы 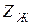 жүктеменің кедергісі еркінше болса
жүктеменің кедергісі еркінше болса 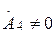 болады, яғни желіде кері толқын пайдалы болады.
болады, яғни желіде кері толқын пайдалы болады.
Бұл жағдайда комплекстік шағылу коэффициенті арқылы есепке алуға болады. Комплекстік шағылу коэффициент 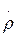 - желінің қандай да болған нүктесіндегі кері және тура толқынлардың комплексті кернеулермен токтардың өзара қатынасы:
- желінің қандай да болған нүктесіндегі кері және тура толқынлардың комплексті кернеулермен токтардың өзара қатынасы:
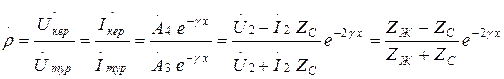 (13.37)
(13.37)
Кері толқын жоқ кезде желінің аяғына тура толқынмен жеткізілетін барлық қуат жүктемеде сіңіріледі. Кері толқын бар кезде тура толқынның қуат бөлігі кері толқынмен энергия көзіне қайтарылады.
13.7 Желінің келіскен жүктемесі
Егер де желінің аяғында толқынды кедергіге тең жүктеменің кедергісі қосылған болса, яғни 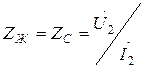 , онда
, онда 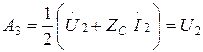 және
және 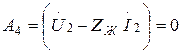 болады да, кері толқын тумайды. Мұндай жүктемені келіскен деп атайды. Бұл жағдайда шағылу коэффициенті
болады да, кері толқын тумайды. Мұндай жүктемені келіскен деп атайды. Бұл жағдайда шағылу коэффициенті 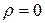 .
.
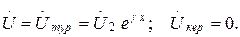 (13.38)
(13.38)
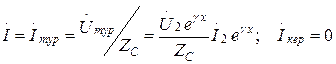 (13.39)
(13.39)
Бұдан шығады 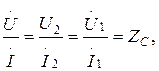
яғни желінің қандай да болған нүктесі үшін 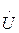 және
және 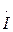 комплекстердің қатынасы
комплекстердің қатынасы 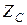 толқынды кедергіге тең.
толқынды кедергіге тең.
(13.33) теңдеуден шығады: келіскен желі үшін 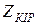 =
= 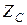 .
.
Желінің аяғындағы кернеудің басты фазасы нөлге тең деп алсақ, яғни 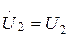 тең деп, (13.38) және (13.39) негізінде желінің қандай да болған нүктесінде кернеумен токтың лезді мәндерін жазамыз:
тең деп, (13.38) және (13.39) негізінде желінің қандай да болған нүктесінде кернеумен токтың лезді мәндерін жазамыз:
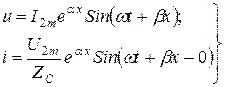 (13.40)
(13.40)
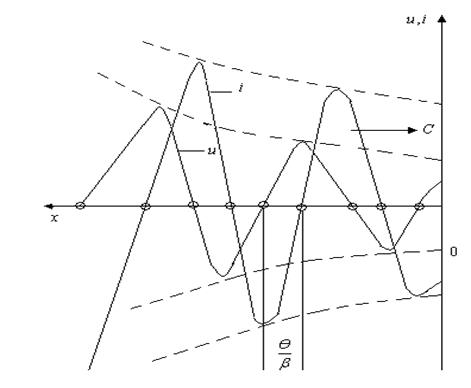
13.5-сурет
Ток кернеудің 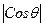 бұрышқа озады.
бұрышқа озады.
Желінің қандай да болған кесіндісіндегі қуат
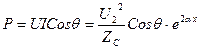 (13.41)
(13.41)
Келіскен желіден берілетін қуат табиғи немесе натуралды деп аталады.
500, 220, 110 және 35 кВ кернеуі бар желілер үшін табиғи қуат 600, 120, 30 және 3 МВт тең.
Желінің алатын қуаты 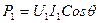 , желінің аяғындағы қуат
, желінің аяғындағы қуат 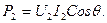
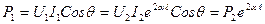 (13.42)
(13.42)
Желінің ПӘК-і
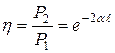 (13.43)
(13.43)
Желінің басынан алыстанған сайын қуат азайды.
Қуат шығындары сымдағы кедергілердегі және оқшаулардың өткізгіштеріндегі шығындардың қосындысына тең.
13.8 Бұрмалауы жоқ желі
Байланыс желімен берілетін дабылдар әртүрлі жиіліктердің көпшіліктің жиынтығы: егер де синусоидалды периодикалы дабылдар болса үзінді, ал периодикалы емес дабыл болса үзілмес спектр құрылады.
Егер де желінің басымен аяғындағы дабылдың түрі бірдей болса, онда дабыл берілісі бұрмаланған емес болады.
Бұл жағдай 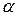 әлсіреу коэффициент және
әлсіреу коэффициент және 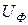 фазалық жылдамдық бірлық жиіліктерде бірдей болса тұрады.
фазалық жылдамдық бірлық жиіліктерде бірдей болса тұрады.
Әртүрлі жиіліктердегі бірдей сөну емес амплитудалық бұрмалауды, толқындардың әртүрлі жиіліктерде жылдамдықтарының бірдей емес болуы фазалық бұрмалауды тудырады.
Бұрмаланған емес беріліс үшін 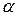 жиіліктен тәуелсіз, ал
жиіліктен тәуелсіз, ал 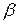 жиілікке тура пропоционалды болуы керек. Ақырғы жағдайда фазалық жылдамдық
жиілікке тура пропоционалды болуы керек. Ақырғы жағдайда фазалық жылдамдық 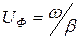 жиілікке тәуелді болмайды. Мұндай жағдайда мынадай теңдік орындалса болады
жиілікке тәуелді болмайды. Мұндай жағдайда мынадай теңдік орындалса болады
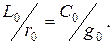 (13.44)
(13.44)
Тарату коэффициенті 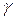 тең:
тең:
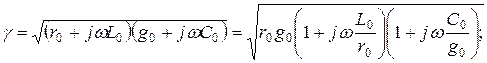
(13.44) есепке алып, табамыз
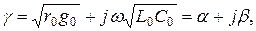 (13.45)
(13.45)
яғни әлсірету коэффициент 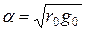 -жиіліктен тәуелсіз, ал фазалық коэффициент
-жиіліктен тәуелсіз, ал фазалық коэффициент 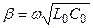 -жиілікке тура пропорционалды.
-жиілікке тура пропорционалды.
Параметрларі (13.44) теңдеуді қанағат ететін желіні бұрмалауы жоқ желі деп атайды.
Бұрмалауы жоқ желінің толқынды кедергісі – нақтылы сан, яғни жиіліктен тәуелсіз активтік кедергі
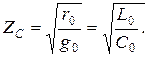 (13.46)
(13.46)
Фазалық жылдамдықта жиіліктен тәуелсіз

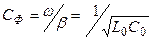 . (13.47)
. (13.47)
Желінің толқынды кедергісі активтік болғандықтан 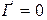 .
.
Кернеулердің және токтардың лезді мәндерінің желінің қатынасы болған нүктелерінде тең:
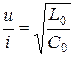 , ал бұдан шығады
, ал бұдан шығады 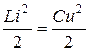 . (13.48)
. (13.48)
Сондықтан келіскен жүктемесі бар бұрмалауы жоқ желінің қандай да болған бөлігінде әрбір уақытта магнит өрістің энергиясы электр өрістің энергиясына тең.
(13.44) жағдай орындау үшін желіге белгілі аралық сайын жасанды индуктивтікті үлкейту үшін индуктивтік орауыштарды қосу керек немесе өткізгіш талсымдары жоғары магниттік өтімділігі бар заттардан жасалған кабельдерді қолдану керек.
13.9 Шығындары жоқ желі
Желіде энергия шығындарды азайту үшін активтік кедергі 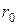 және оқшалаудың өткізгіштігі
және оқшалаудың өткізгіштігі 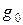 неғұрым аз болуы керек.
неғұрым аз болуы керек.
Ауалық желілерде индуктивтік кедергі 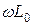 активтік кедергіден
активтік кедергіден 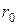 үлкен болады, ал сыйымдылық өткізгішті
үлкен болады, ал сыйымдылық өткізгішті 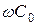 активтік өткізгіштен
активтік өткізгіштен 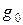 үлкен болады. Жиілік өскен кезде бұл айырмашылық одан әрі өседі.
үлкен болады. Жиілік өскен кезде бұл айырмашылық одан әрі өседі.
Активтік кедергісі 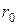 және активтік өткізгіштігі
және активтік өткізгіштігі 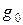 нөлге тең деп алынатын желілер шығындары жоқ желі деп аталады.
нөлге тең деп алынатын желілер шығындары жоқ желі деп аталады.
Бұл жағдайда желінің екіншілік параметрлерінің түрі:
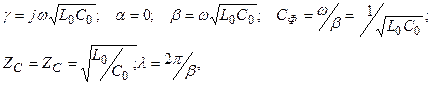
яғни шығыны жоқ желіде толқындар әлсіремейді, толқынды кедергі активтік, ал фазалық жылдамдық жиілікке тәуелді емес.
Екі сымды желінің ұзындық бірлігінің сыйымдылығы, 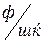 :
:
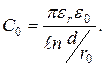 (13.49)
(13.49)
Сол желінің ұзындық бірлігінің индуктивтігі, 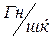 :
:
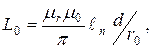 (13.50)
(13.50)
мұндағы 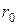 - сымның радиусы, d- сымдардың біліктерінің арасындағы аралық.
- сымның радиусы, d- сымдардың біліктерінің арасындағы аралық.
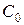 және
және 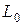 мәндері
мәндері 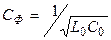 қойып, табамыз
қойып, табамыз
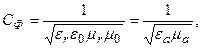 (13.51)
(13.51)
мұндағы 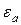 және
және 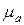 -сымдар арасындағы ортаның абсолюттік диэлектрикалық және магниттік өтімділіктері.
-сымдар арасындағы ортаның абсолюттік диэлектрикалық және магниттік өтімділіктері.
Вакуумда жарықтық жылдамдығы
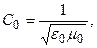 (13.52)
(13.52)
онда фазалық жылдамдық үшін жазуға болады
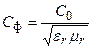 . (13.53)
. (13.53)
Толқынды кедергінің аргументі Ө нөлге тең, яғни тура және кері толқынды токтар кернеулермен дәл түседі.
Шығындары жоқ желінің комплекстік аргументтінен гиперболикалық функциялар ұзын желінің теңдеулері нақтылы аргументтен айналма функциялар теңдеулерге көшеді.
Егер де желінің басындағы кернеу 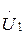 және ток
және ток 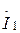 берілсе, онда
берілсе, онда
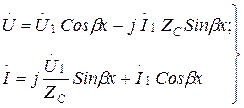 (13.54)
(13.54)
Егер де желінің аяғындағы кернеу 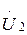 және ток
және ток 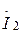 берілсе, онда
берілсе, онда
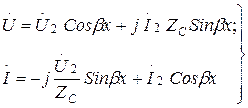 (13.55)
(13.55)
Желінің кіріс кедергісі
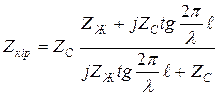 (13.56)
(13.56)
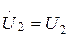 және
және 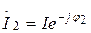 кезінде лезді мәндерге өтетін болсақ
кезінде лезді мәндерге өтетін болсақ 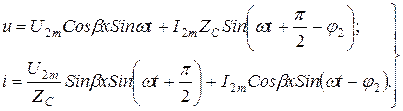 (13.57)
(13.57)
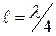 және
және 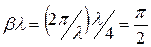 кезінде, шығады
кезінде, шығады
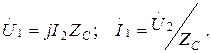 (13.58)
(13.58)
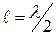 және
және 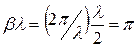 кезінде, шығады
кезінде, шығады
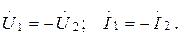 (13.59)
(13.59)
13.10 Тұйық толқындар
Шығыны жоқ желінің аяғында бос жүріс, қысқа тұйықталу кезінде және таза реактивтік жүктеме кезде активтік қуат нөлге тең болады.
1 Бос жүріс ереже 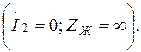
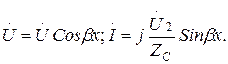 (13.60)
(13.60)
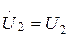 кезінде кернеудің және токтың лезді мәндері тең
кезінде кернеудің және токтың лезді мәндері тең
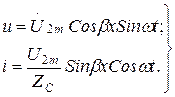 (13.61)
(13.61)
Бұл тұйық толқындардың теңдеулері
Тұйық толқынның теңдеуінің біреуі уақыттан, екіншісі координатадан тәуелді екі функцияның көбейтіндісі.
Тұйық толқын деп амплитудалары бірдей тура және кері толқындардың бір-біріне салу процесін атайды.
Шынында, 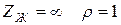 және
және 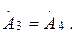
Кернеуді амплитудалары бірдей тура және кері толқындардың кернеулерінің қосындасы, токтарды-айырма түрінде көрсетуге болады.
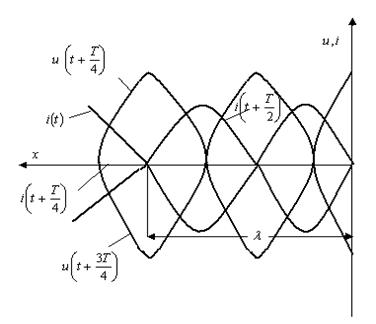
13.6-сурет
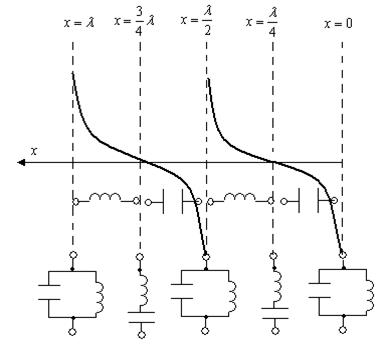
13.7-сурет
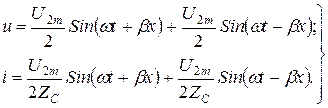 (13.62)
(13.62)
Бос жүріс ережеде желінің аяғында 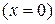 және аяқтан
және аяқтан 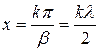 (мұндағы К- бүтін сан) аралықта тұратын нүктелерде қандай да болған уақыт мезгілде пучность деп аталатын кернеудің максимумдары және токтың түйіндері байқалады. Токтың және кернеудің түйіндері және пучнестері орындарынан қозғалмайды.
(мұндағы К- бүтін сан) аралықта тұратын нүктелерде қандай да болған уақыт мезгілде пучность деп аталатын кернеудің максимумдары және токтың түйіндері байқалады. Токтың және кернеудің түйіндері және пучнестері орындарынан қозғалмайды.
Шығындары жоқ ажыратылған желінің кіріс кедергісі
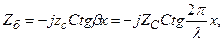 (13.63)
(13.63)
яғни таза реактивтік, ал оның мінезі желінің ұзындығымен және жиілікпен белгіленеді. Абсолюттік шамамен және мінездің өзгеруінің желінің ұзындығынан тәуелдігі 13.7-суретте көрсетілген х=0 – ден 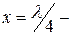 ге дейін,
ге дейін, 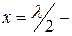 ден
ден 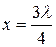 -ге дейін және сол сияқты желі сыйымдылық кедергі болады, ал
-ге дейін және сол сияқты желі сыйымдылық кедергі болады, ал 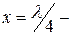 тен,
тен, 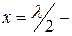 дейін,
дейін, 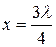 -ден
-ден 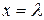 және сол сияқты желі индуктивтік кедергі.
және сол сияқты желі индуктивтік кедергі. 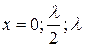 және сол сияқты желі-параллельді резонанстық контур, ал
және сол сияқты желі-параллельді резонанстық контур, ал 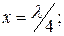
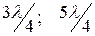 және сол сияқты желі тізбекті резонанстық контур.
және сол сияқты желі тізбекті резонанстық контур.
Қысқа тұйықталу кезде 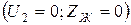 шығады:
шығады:
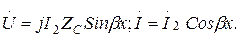 (13.64)
(13.64)
Лезді мәндер
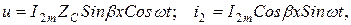 (13.65)
(13.65)
яғни кернеумен ток – тұйық толқындар
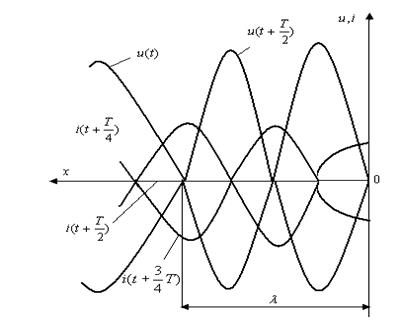
13.8-сурет
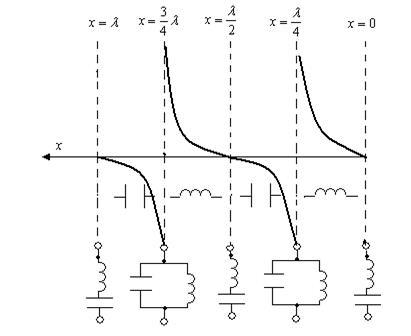
13.9-сурет
Әртүрлі уақыт мезгіл үшін желінің аяғында 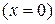 және аяғынан
және аяғынан 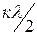 аралықта жататын нүктелерде кернеудің түйіні және токтың пучнісі болады, ал желінің аяғынан
аралықта жататын нүктелерде кернеудің түйіні және токтың пучнісі болады, ал желінің аяғынан 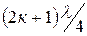 аралықта жататын нүктелерде кернеудің пучнісі және токтың түйіндері болады (13.8-сурет).
аралықта жататын нүктелерде кернеудің пучнісі және токтың түйіндері болады (13.8-сурет).
Кернеудің пучнісі және тоқың түйіні бір-бірінен толқынның ұзындығының бір шірекке ығысқан.
Шығындары жоқ қысқа тұйықталған желінің кіріс кедергісі
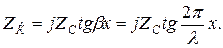 (13.66)
(13.66)
яғни таза реактивтік, желінің ұзындығына және жиіліке тәуелді индуктивтік немесе сыйымдылықты болуы мүмкін. Қысқа тұйықталған желінің ұзындығына тәуелді кіріс кедергінің өзгеруі 13.9-суретте көрсетілген. Суреттен көрініп тұр: 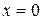 -ден,
-ден, 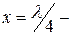 ге дейін,
ге дейін, 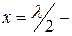 ден
ден 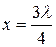 -ге дейін желі индуктивтік кедергі, ал
-ге дейін желі индуктивтік кедергі, ал 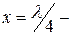 тен,
тен, 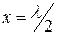 ,
, 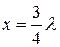 -ден,
-ден, 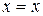 -ге дейін –сыйымдылық кедергі,
-ге дейін –сыйымдылық кедергі, 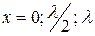 ж.с.с. желі –параллельді резонанстық контур.
ж.с.с. желі –параллельді резонанстық контур.
Жүктемемен келіскен желіні құру үшін қабылдағышқа тізбектеп немесе параллельді индуктивтік немесе сыйымдылық элементтерді қосу керек. Мұндай элементтер ретінде жоғары жиілік кезде қысқа шығыны жоқ тұйықталған немесе ажыратылған желіні пайдалануға болады.
Сыйымдылық элементі ретінде ұзындығы 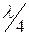 тең ажыратылған желіні, ал индуктивтік элемент ретінде ұзындығы
тең ажыратылған желіні, ал индуктивтік элемент ретінде ұзындығы 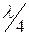 тең қысқы тұйықталған желіні таңдайды.
тең қысқы тұйықталған желіні таңдайды.
Шығыны жоқ ажыратылған желінің х ұзындығын 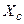 берілген кезде мынадағы кейіптеме бойынша анықтауға болады
берілген кезде мынадағы кейіптеме бойынша анықтауға болады
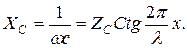 (13.67)
(13.67)
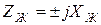 кезде, яғни таза реактивтік жүктеме кезде желіде тағы да тұйық толқындар болады. Бірақ та желінің аяғында кернеудің және токтың пучності және түйіні болмайды.
кезде, яғни таза реактивтік жүктеме кезде желіде тағы да тұйық толқындар болады. Бірақ та желінің аяғында кернеудің және токтың пучності және түйіні болмайды.
Түйінде ток немесе кернеу нөлге тең, онымен бірге қуатта нөлге тең, ал сол себептен түйін арқылы энергия өтпейді.
Дата добавления: 2017-01-29; просмотров: 1360;
