Симметриялық құраушылар әдісі 7 страница

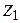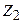және төменгі жиілікті сүзбе үшін мәндерін қойғаннан кейін шығады

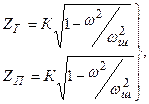(12.3)

мұндағы .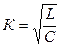

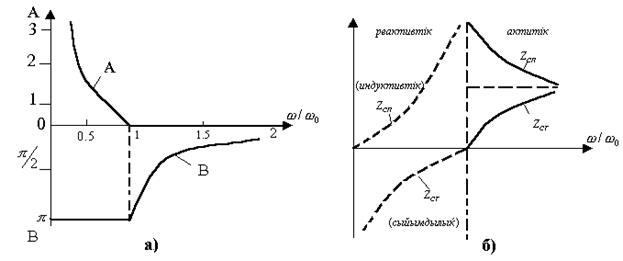
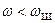кезде, яғни өткізу алқапта 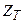және 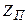- реактивтік кедергілер, жиілік өскенде нөлден 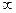-ге дейін Т-сияқты және 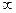-тен нөлге дейін П-сияқты сүзгілерде өзгереді.

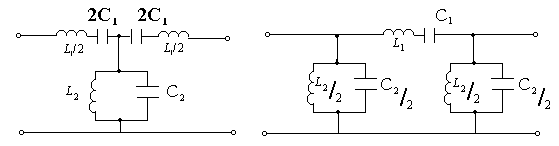
12.6 – сурет 12.7 – сурет

Сүзгінің индуктивтігімен сыйымдылығын есептеген кезде шекті жиілік (12.2) және К тең жүктеменің кедергісі тапсырылады;

б) жоғарғы жиіліктердің сүзгілері.

12.6 – суретте К түрлі Т- және П- сияқты сүзгілердің жоғарғы жиіліктердің дабылдардың өткізіп төменгі жиіліктердің дабылдардың ұстап қалатын сүлбілері келтірілген.

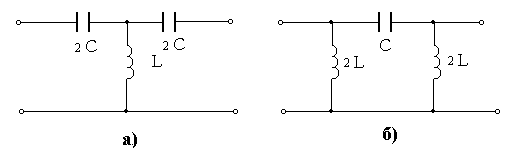
12.7 – сурет

.

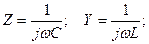
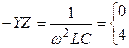Өткізу алқап мына шекаралықтарда жатады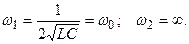

12.8 – сурет

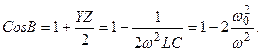
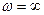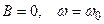кезде кезде 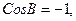сондықтан .

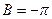Т- және П- сияқты сүлбілер үшін сипаттамалы кедергілер

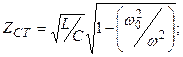
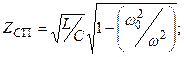(12.4)

Өткізу алқапта Z_СТ және Z_СП кедергілер активтік. Z_СП 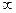-тен 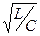-ге дейін, ал Z_СТ нөлден 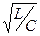-ге дейін өзгереді.

Сүзгіні жүктемемен келістіру үшін жүктеменің кедергісі активтік болу керек және 4.7,б – суретте көрсетілген сияқты өзгеру керек;

в) алқапты өткізгіш сүзгілер.

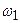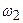Егер де 14.5 және 14.7 суреттердегі сүзгілердің сүлбілерін электр бір-бірімен қосқан сияқты болса, онда пайда болған сүзгі - ден - ге дейін ауқымдағы дабылдарды өткізеді.

а) б)

12.9 – сурет

Бір жиілік кезде Z бойлық кедергілер (кернеу резонансы) және Y көлденен өткізгіштер (токтар резонансы) нөлге тең болу үшін мына шарт орындалу керек.

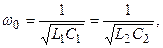(12.5)

бұл жағдайда .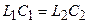

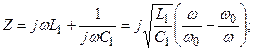
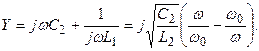(12.6)

Өткізу алқаптың шекараларын белгілейтін теңдеулер

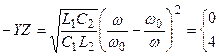(12.7)

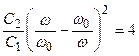теңдеуді шешу керек, немесе

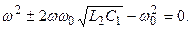
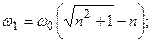
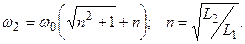(12.8)

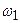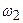Табылған өрнектерден сүзгі жиілік -ден -ге дейін өзгерген кезде дабылдарды өткізетіндігі шығады (12.10,а – сурет).

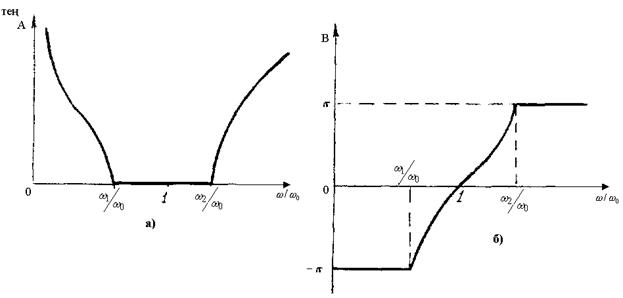
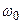жиілік шегаралық жиіліктердің орташасына, яғни .

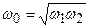12.10 – сурет

Сөну (әлсіреу) коэффициенттің басу алқаптағы жиілік тәуелділігі мына өрнек арқылы табылады

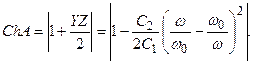(12.9)

Бұл теңдеу бойынша 12.10,а – суретте 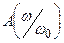жиілік сипаттама салынған.

Өткізу алқаптағы В фаза коэффициенттің тәуелділігін былай белгілейміз

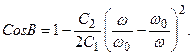(12.10)

Екі сүлбедегі сипаттамалы кедергілер:

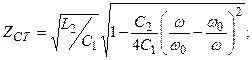
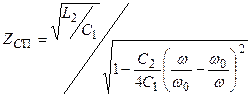. (12.11)

Z_CT және Z_CП кедергілердің 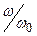тәуелділіктері 14.11,а,б – суреттерде көрсетілген.

12.11 – сурет

Жүктеменің кедергісі сипаттамалы кедергіге тең қылып аламыз, яғни .

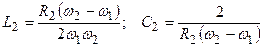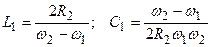. ; (12.15)

г) бөгегіш сүзгілер.

Егер де алқапты өткізгіш сүзгілердің сүлбілерінде сыйымдылықтардан және индуктивтіктерден құрылған параллельді және тізбектеп қосылған тармақтарды орындарымен алмастырсақ, онда пайда болған сүзбелердің сүлбілерінде 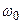жиілігін кезде Z бойлық кедергілердің үзілді және Y көлденен өткізгіштердің қысқа түйықталуы пайда болады.

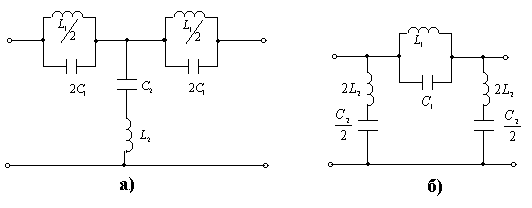
12.12 – сурет

Ол үшін мына шартты орындауы керек:

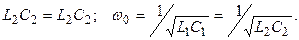
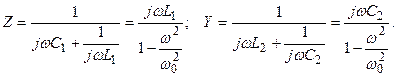
Өткізу алқаптың шекараларына мына теңдеулерден табамыз

.

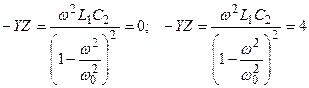Бірінші теңдеуден ; ,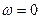

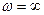Екінші теңдеуден 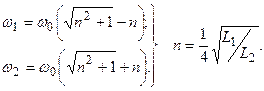(12.16)

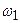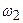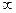Табылған өрнектерден шығады - сүзгі 0-ден -ге дейін және -ден -ге дейін жиіліктерді өткізеді. .

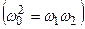Бөгеу алқапта сыну коэффициенттін жиілік тәуелділігі мына өрнектен табылады

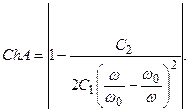(12.17)

Өткізу алқапта сүзгінің фазалық сипаттаманың теңдеуі:

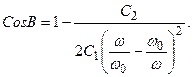(12.18)

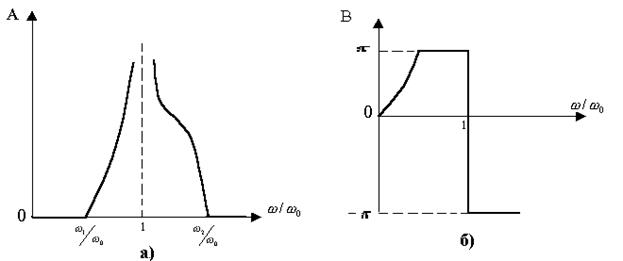
12.13 – сурет

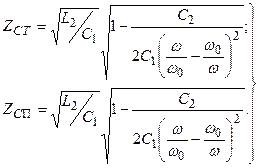(12.19)

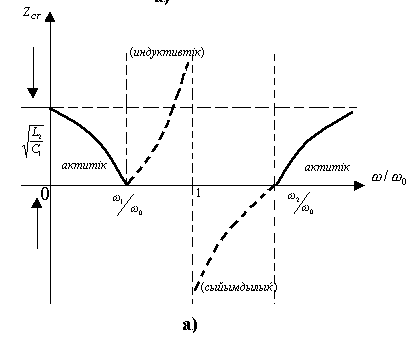
12.14 – сурет

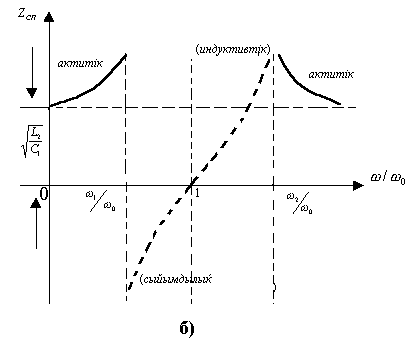
12.14 – сурет

Бұл теңдеулер бойынша 12.14,а,б – суреттерде Z_CT және Z_СП 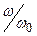-ден тәуелділіктер салынған. 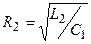, яғни жүктеме келіскен.

.

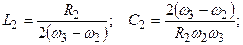
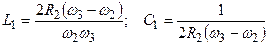Он үшінші тарау

13 Параметрлері таратылған тізбектер

13.1 Ұзын желілердегі токтар және кернеулер

Электр энергетикада үлкен кернеулер кезінде және электр байланыста үлкен жиіліктер кезінде, сонымен бірге электр жеткізу желінің ұзындығы үлкен болғанда ығысу және кему токтармен елемеуге болмайды.

Сымдарғы токтар кедергілерде кернеу түсуді құрады және айнымалы магнит өрісті құрады. Бұл өріс барлық желінің бойында өздік электр қозғаушы күшті өндейді. Сондықтан, сымдарының арасындағы кернеуде тұрақты болып қалмайды.

Желіні бойлай токтың және кернеудің өзгеруін есептеу үшін желінің әрбір қандай да болған кішкентай элементтің кедергісі және индуктивтігі, ал сымдар арасында - өткізштік және сыйымдылығы бар, яғни желіні параметрлері таратылған тізбек деп қарау керек. Мұндай желі ұзын желі деп аталады.

Кедергі, индуктивтік, өткізгіштік және сыйымдылық желінің ұзындығы бойынша біркелкі таратылған деп есептейміз. Мұндай желіні біртекті деп атайды.

13.2 Біртекті екі сымды желінің теңдеулері

Екі сымды желінің кез келген кескіндісінде токтарға және кернеулерге сәйкесті дифференциалды теңдеулерді құрамыз.

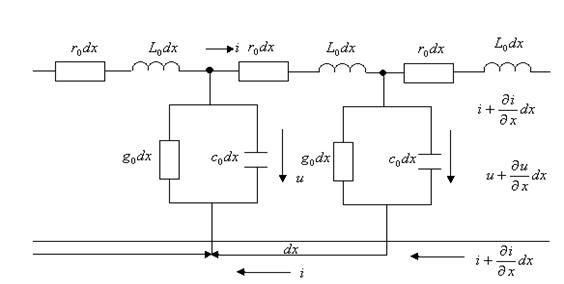
13.1-сурет

Жоғары сым тура сым, төменгі сым кері сым деп аталады. Біртекті желінің оның ұзындық бірлігіне жататын біріншілік параметрлері белгілі болсын: 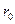- тура және кері сымдардың кедергілері 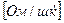; 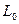-тура және кері сымдармен құрылатын ілмектің индуктивтігі 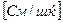; 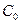- сымдар арасындағы сыйымдылық .

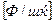Ұзын желіні өте көп ұзындығы 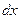тең элементердің тізбекті қосылған түрде көрсетуге болады. Әрбір элементтің 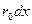кедергісі, 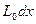идуктивтігі, 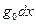өткізгіштігі және 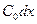сыйымдылығы бар (13.1-сурет).

Желінің басынан элементке дейін аралықты 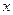деп белгілейміз. Кирхгофтың заңдары бойынша 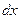ұзындығы бар элемент үшін жазамыз:

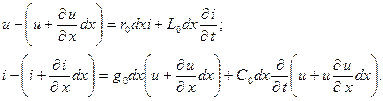
Екіншілік дәрежелі шамаларды еске алмай және 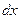қысқартып дифферинциалды теңдеулерді табамыз:

(13.1)

(13.2)

Белгілі басты және шеғаралық жағдайлар кезде теңдеулердің жүйесін шешу токты және кернеуді желінің ұзындығының және уақыттың функциялары ретінде белгілеуге рұқсат береді.

13.3 Біртекті желідегі қалыптасқан ереже

(13.1) және (13.2) теңдеулерді қалыптасқан ереже жасап және комплексті токтарды, кернеулерді, кедергілерді және өткізгіштерді кіргізіп табамыз

(13.3)

(13.4)

мұндағы 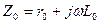және 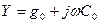- ұзындықтың бірлігінде комплекстік кедергі және комплекстік өткізгіштік. (13.3) және (13.4) теңдеулерді дифференциялаймыз:

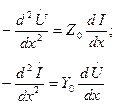ал содан кейін 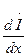және 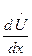(13.3) және (13.4) бойынша алмастырып табамыз:

(13.5)

(13.6)

(13.5)- тұрақты коэффициенттері бар екінші дәрежелі сызықты дифференциалды теңдеу. Оның шешуі мына түрде болады:

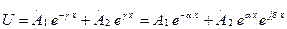, (13.7)

мұндағы

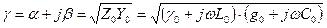, (13.8)

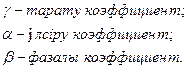
-интегралдаудың комплексті тұрақтылары. (13.3) бойынша ток 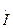тең

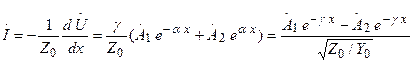. (13.9)

Өлшемі кедергіге тең (13.9) теңдеудің бөлгіші 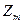толқынды кедергі деп аталады. Біртекті желі үшін (төртұштық үшін) толқынды кедергі сипаттамалы кедергімен дәл түседі.

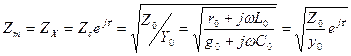, (13.10)

мұндағы

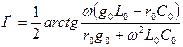. (13.11)

Толқынды кедергі 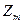және тарату коэффициент 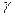біртекті желінің екіншілік параметрлері деп аталады. 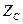(13.9) теңдеуге қойып жазамыз:

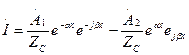. (13.12)

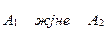(өлшемдері – кернеу) көрсеткіш түрде көрсетіп 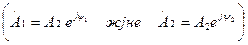, кернеулерді және токтардың лезді мәндерін жазамыз:

(13.13)

(13.14)

Теңдеулердің оқ жағындағы әрбір қосындыны координата х өсу және кему бағытына қарай жүгіріп бара жатқан толқын деп қарауға болады. Бұл толқындар қозғалыстың бағытына қарай сөнеді. Әрбір қосында қандай да болған бекітілген 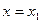нүктеде периодикалы синусоидалы уақыт функциясы болады, ал бекітілген 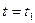уақыт мезгілде бұл қосындылар сөніп бара жатқан желі бойындағы тербелену болады (яғни х өзгерген кезде).

Жүгіріп бара жатқан толқынның негізгі сипаттамалары фазалық жылдамдық және толқынның ұзындығы.

Толқынның 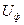фазалық жылдамдығы деп тербеленудің фазасының ауыспалалық жылдамдығы аталады. Бұл жылдамдық уақыт өзгерген кезде және х аралық өскен кезде тұрақты болып қалады, яғни

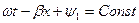ал бұдан шығады

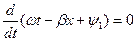және 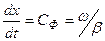. (13.15)

(13.13) теңдеудің оң жағындағы екінші қосындыны зерттегенде фазалық жылдамдықтың мәні сол сияқты бірақ таңбасы кері болады. Бұдан шығады- қосындылар қарама-қарсы бағыттарда қозғалып бара жатқан толқындар.

Толқынның ұзындығы 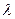деп тербелену фазалары 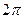-ге айырылатын толқынның таралу бағытына қарай алынған екі ең жақын жатқан нүктелердің арасындағы аралық.

.

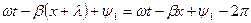Бұдан шығады 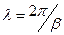және 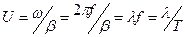, (13.16)

Яғни период Т тең уақытта толқын толқынның ұзындығына тең аралықты жүгіріп өтеді.

Желінің басынан қозғалап келе жатқан толқынды тура, ал аяғынан қозғалып келе жатқан толқынды кері деп атайды.

13.1-суретте тура сөніп бара жатқан толқын көрсетілген

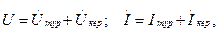(13.17)

мұндағы 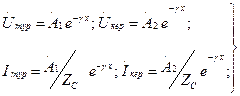(13.18)(13.19)

Тура және кері толқындардың токтарымен кернеулері Ом заңымен байланысқан

(13.20)

Табылған нәтижелер үш фазалы желілерге де қолданылады. Бұл жағдайда U және I – фазалық кернеу және ток, ал 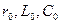және 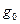бір фазаға жатады.

13.1 мысал. Үш фазалы электр жеткізу желінің ұзындығы 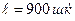, кернеуі 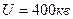, жиілігі 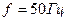.Біріншілік параметрлердің келесі шамалары бар: .

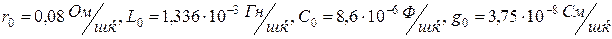Екіншілік параметрлерді, толқынның ұзындығы және фазалық жылдамдықты белгілеу керек.

1 шқ. комплекстік кедергі және өткізгіштік:

;

.

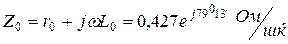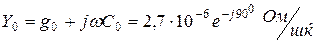Жиілік сипаттамалары:

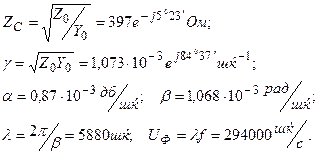
13.4 Гиперболикалық функцияларда біртекті желінің теңдеулері

және тұрақтыларын білу үшін шекаралық жағдайлар белгілі болу керек.

Желінің басында 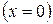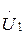кернеу және 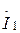ток берілген болсын. (13.7) және (13.12) теңдеулерден 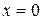кезде шығады:

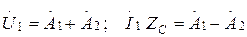, ал бұдан

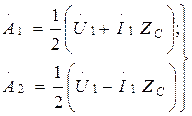(13.21)

(13.7) және (13.12) теңдеулерге және мәндері қойып желінің қандай да болған нүктесінде (желінің басынан Х аралықта) 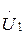кернеу және 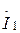үшін табамыз:

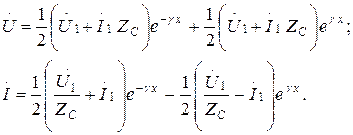
Оң жақтағы мүшелерді топтастарып және 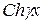пен 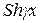гиперболикалық функцияларды кіргізіп табамыз:

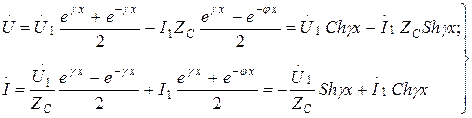(13.22)

Бұл теңдеулер желінің басындағы шамалары бойынша желінің қандай да болған нүктесіндегі кернеумен токты белгілеуге рұқсат етеді.

Енді желінің аяғындағы 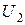кернеу және 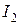ток берілген болсын, ал бұл жағдайда жүктеменің кедергісі 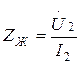белгілі болады.

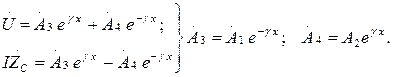(13.23)

(13.23) ден 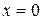кезде табамыз:

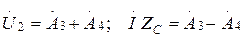, ал бұдан шығады

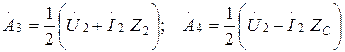(13.24)

(13.24) ті (13.23) –ге қойып, мүшелерді топтастырып және 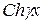пен 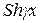гиперболикалық функцияларды кіргізіп табамыз:

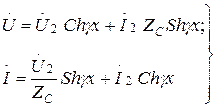(13.25)

Тұрақты ток желілер үшін :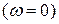

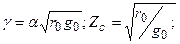(13.26)

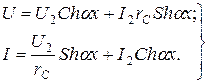(13.27)

13.2 мысал 13.1 мысалдың нәтижелері бойынша белгілеу керек:

1 желінің аяғында токты;

2 желінің басындағы кернеуді және токты;

3 желінің басында және аяғында кернеумен токтың арасындағы фазалық ығысуды;

4 желінің ПӘК-тің, егер де желінің аяғында белгілі:

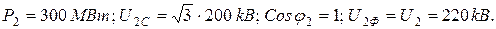
1 Желінің аяғындағы ток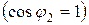

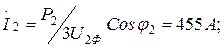
2 Комплекстік ауыспалыдан 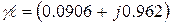гиперболикалық функциялардың мәндерін кестеден немесе калькулятор арқылы табамыз