Симметриялық құраушылар әдісі 6 страница
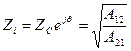 (11.16)
(11.16)
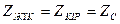 кездегі төртұштықтың ережесін жүктеме келіскен ереже деп атайды. Егер де көздің ішкі кедергісі
кездегі төртұштықтың ережесін жүктеме келіскен ереже деп атайды. Егер де көздің ішкі кедергісі 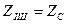 болса, онда көріктендіру көзде төртұштықпен келіскен деп есептеледі. Бұл ережеде
болса, онда көріктендіру көзде төртұштықпен келіскен деп есептеледі. Бұл ережеде 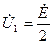 және
және 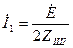 (11.17)
(11.17)
Симметриялы төртұштықтың, кірістегі және шығыстағы кернеулерді және тоқтарды бір-бірімен салыстыру өте жеңіл өткізуге рұқсат беретін, екінші параметрды алады.
Жүктеме келіскен кезде
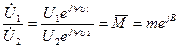 (11.18)
(11.18)
мұндағы 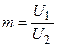 - кернеудің шамасын өзгергенді көрсететін қатынастың модулі;
- кернеудің шамасын өзгергенді көрсететін қатынастың модулі; 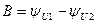 - кірістің және шығыстағы кернеулердің арасындағы фазалардың ығысуын көрсететін аргумент. Бұл бұрыш фазаның тұрақтысы деп аталады. Кірістегі және шығыстағы кернеулер бір-бірінен өте айрықша болады. Сондықтан, кіріспен шығыстағы кернеулер қатынасындағы логарифмдік масштабы бағаланады, яғни
- кірістің және шығыстағы кернеулердің арасындағы фазалардың ығысуын көрсететін аргумент. Бұл бұрыш фазаның тұрақтысы деп аталады. Кірістегі және шығыстағы кернеулер бір-бірінен өте айрықша болады. Сондықтан, кіріспен шығыстағы кернеулер қатынасындағы логарифмдік масштабы бағаланады, яғни 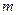 орнына әлсіретудің тұрақтысы пайдаланады
орнына әлсіретудің тұрақтысы пайдаланады 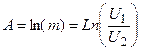 немесе
немесе 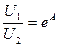 (11.19)
(11.19)
Әлсірету тұрақтының өлшемі – непер (Нп). Төртұштықтың 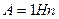 тең, егер де жүктеме келіскен кезде шығыстағы кернеу кірістегі кернеуден
тең, егер де жүктеме келіскен кезде шығыстағы кернеу кірістегі кернеуден 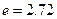 есе аз болса
есе аз болса
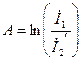 (11.20)
(11.20)
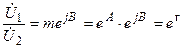 (11.21)
(11.21)
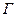 – комплексті мөлшемсіз шама жүктеме келіскенде кернеудің және тоқтың өзгергендегі мәндерін фаза бойынша сипаттайды да төртұштықтың беріліс тұрақтысы деп аталады.
– комплексті мөлшемсіз шама жүктеме келіскенде кернеудің және тоқтың өзгергендегі мәндерін фаза бойынша сипаттайды да төртұштықтың беріліс тұрақтысы деп аталады. 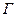 төртұштықтың құрылымын құрайтын элементтердің параметрлерімен толық анықталады.
төртұштықтың құрылымын құрайтын элементтердің параметрлерімен толық анықталады.
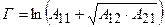 (11.22)
(11.22)
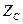 сипаттамалы кедергіні және берілістің тұрақтысын симметриялы төртұштықтың екіншілік параметрлері деп атайды.
сипаттамалы кедергіні және берілістің тұрақтысын симметриялы төртұштықтың екіншілік параметрлері деп атайды.
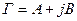 формула бойынша есептелген кезде
формула бойынша есептелген кезде 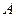 -ны непермен,
-ны непермен, 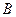 -ны радианмен қояды.
-ны радианмен қояды.
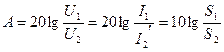 (децибелл).
(децибелл).
11.5 Төртұштықтың теңдеулері гиперболикалық функциялар түрінде
Симметриялы пассивтік төртұштық өте жиі екіншілік параметрлерімен тапсырылады. Бұл жағдайда, ережені зерттеген кезде кернеулер және тоқтар екіншілік параметрлермен байланысқан теңдеулерді пайдалану керек.
Мұндай теңдеулерді құрастыру үшін 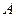 коэффициентерді екіншілік параметрлер арқылы көрсетіп (10.1) теңдеуге қою керек.
коэффициентерді екіншілік параметрлер арқылы көрсетіп (10.1) теңдеуге қою керек.
(10.22) теңдеуден шығады
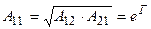 (11.23)
(11.23)
Симметриялы төртұштық үшін байланыс теңдеу
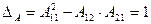 (11.24)
(11.24)
(11.24) және (11.26) теңдеулерді 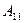 және
және 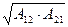 қатысты шешім, табамыз:
қатысты шешім, табамыз:
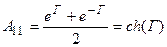 ;
; 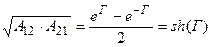 (11.25)
(11.25)
(11.25) (10.1) қойғаннан кейін симметриялы төртұштықтың гиперболикалық түрде теңдеулерін табамыз
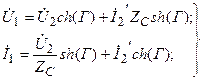 (11.26)
(11.26)
Симметриялы төртұштық кіріс кедергісі
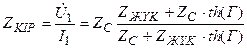 (11.27)
(11.27)
Қысқа тұйықталған кезде ( 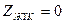 )
)
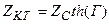 (11.28)
(11.28)
Бос жүріс кезде ( 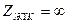 )
)
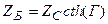 (11.29)
(11.29)
(11.28) және (11.29) екіншілік параметрлерді табамыз
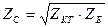 ;
; 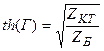 (11.30)
(11.30)
11.6 Төртұштықтың шеңберлік диаграммасы
Біріншілік тізбектегі 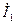 тоқпен екіншілік тізбектегі
тоқпен екіншілік тізбектегі 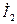 тоқ арасындағы қатынас мынаған тең
тоқ арасындағы қатынас мынаған тең
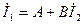 (11.31)
(11.31)
мұндағы 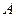 және
және 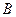 - комплексті сандар.
- комплексті сандар. 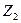 кедергінің
кедергінің 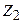 модулі (шамасы) өзгеріп тұр, ал
модулі (шамасы) өзгеріп тұр, ал 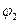 аргумент тұрақты. Бұл жағдайда
аргумент тұрақты. Бұл жағдайда 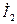 кедергіге қарай тізбекті активтік екіұштық деп қараймыз. Бұл жағдайда
кедергіге қарай тізбекті активтік екіұштық деп қараймыз. Бұл жағдайда 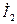 вектор шеңбердің доғасы бойынша жылжиды,
вектор шеңбердің доғасы бойынша жылжиды, 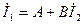 болғандықтан
болғандықтан 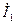 вектордың аяғыда шеңбердің доғасы бойынша жылжиды.
вектордың аяғыда шеңбердің доғасы бойынша жылжиды.

11.9 – сурет
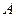 және
және 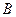 комплекстерді табу үшін
комплекстерді табу үшін 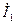 және
және 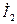 тоқтарды екі ереже кезде білу керек, мысалы
тоқтарды екі ереже кезде білу керек, мысалы 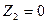 және
және 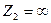 кезде.
кезде. 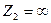 кезде (екіншілік тармақ ажырап тұр)
кезде (екіншілік тармақ ажырап тұр) 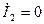 , ал
, ал 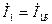 (10.31) бойынша
(10.31) бойынша 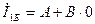 , яғни
, яғни 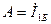 .
. 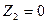 кезде (екіншілік тармақ тұйықталып тұр)
кезде (екіншілік тармақ тұйықталып тұр) 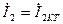 және
және 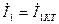 деп белгілеп (10.31) теңдеуге қоямыз да, табамыз.
деп белгілеп (10.31) теңдеуге қоямыз да, табамыз.
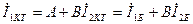 , ал бұдан шығады
, ал бұдан шығады
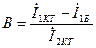
сондықтан, 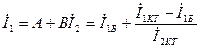 (11.32)
(11.32)
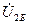 арқылы
арқылы 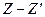 тармақтың ажыратылған қысқыштарындағы кернеуді белгілеп және
тармақтың ажыратылған қысқыштарындағы кернеуді белгілеп және 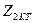 кедергі арқылы активтік екіұштық ретінде қаралып тұрған барлық тізбектің бөлігінің кіріс кедергісін белгілеп эквивалентті генератор принципі бойынша табамыз
кедергі арқылы активтік екіұштық ретінде қаралып тұрған барлық тізбектің бөлігінің кіріс кедергісін белгілеп эквивалентті генератор принципі бойынша табамыз
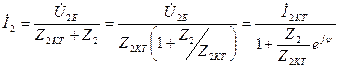 (11.33)
(11.33)
мұндағы 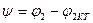
(11.33) теңдеуді (11.32) теңдеуге қойып, табамыз
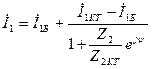 (11.34)
(11.34)
(11.34) теңдеудің екінші қосындысы активтік екіұштық шеңберлік диаграммасының теңдеуі сияқты (хордасы 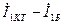 тең). Төртұштықтың шеңберлік диаграммасын құру үшін алдымен
тең). Төртұштықтың шеңберлік диаграммасын құру үшін алдымен 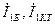 және
және 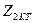 белгілеу керек.
белгілеу керек.
Шеңберлік диаграмманы келесі тәртіппен құрамыз:
1. 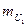 масштабты таңдап
масштабты таңдап 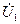 векторды саламыз (10.10 – сурет);
векторды саламыз (10.10 – сурет);
2. 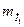 масштабты таңдап
масштабты таңдап 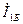 (
( 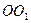 кесінді) векторды және
кесінді) векторды және 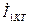 (кесінді
(кесінді 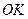 ) векторды саламыз. Шеңберлік диаграмма
) векторды саламыз. Шеңберлік диаграмма 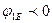 және
және 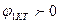 жағдай үшін құрылып жатыр.
жағдай үшін құрылып жатыр.
11.10 – сурет. Төртұштықтың шеңберлік диаграммасы.
3. 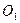 және
және 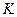 нүктелерді қосып шеңберлік диаграмманың хордасын құрамыз.
нүктелерді қосып шеңберлік диаграмманың хордасын құрамыз.
4. 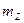 кедергінің масштабты таңдап
кедергінің масштабты таңдап 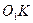 хорда
хорда 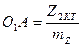 кесіндіні белгілейміз.
кесіндіні белгілейміз.
5. Хорда 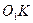 қарай бұрыш
қарай бұрыш 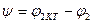 тең ауыспалы параметрлердің түзу сызықты өткіземіз.
тең ауыспалы параметрлердің түзу сызықты өткіземіз.
6. 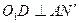 түзу сызықты өткіземіз.
түзу сызықты өткіземіз.
7. Хорданың ортасына перпендикулярдың 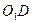 сызықпен кесілген нүкте
сызықпен кесілген нүкте 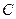 шеңберлік диаграмманың орталығы болады.
шеңберлік диаграмманың орталығы болады.
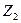 -нің қандай болған мәні үшін
-нің қандай болған мәні үшін 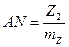 кесіндіні алып
кесіндіні алып 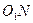 сызықты шеңберлік диаграммасымен
сызықты шеңберлік диаграммасымен 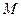 нүктеде қыйысқан жері
нүктеде қыйысқан жері 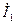 тоқтың векторының аяғының қалыпын көрсетеді.
тоқтың векторының аяғының қалыпын көрсетеді. 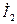 тоқ,
тоқ, 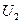 кернеу,
кернеу, 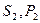 және
және 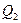 қуаттар екіұштық шеңберлік диаграммасындағы кесінділермен белгіленеді.
қуаттар екіұштық шеңберлік диаграммасындағы кесінділермен белгіленеді. 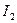 тоқ
тоқ 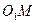 кесіндімен,
кесіндімен, 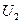 кернеу
кернеу 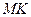 кесіндімен, ал
кесіндімен, ал 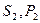 және
және 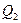 қуаттар
қуаттар 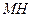 , немесе оған пропорционалды
, немесе оған пропорционалды 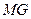 кесіндімен анықталады.
кесіндімен анықталады.
Диаграммада 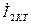 тоққа және
тоққа және 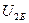 кернеуге
кернеуге 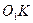 хорда сәйкес, сол себептен
хорда сәйкес, сол себептен 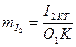 және
және 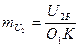
Мысал:
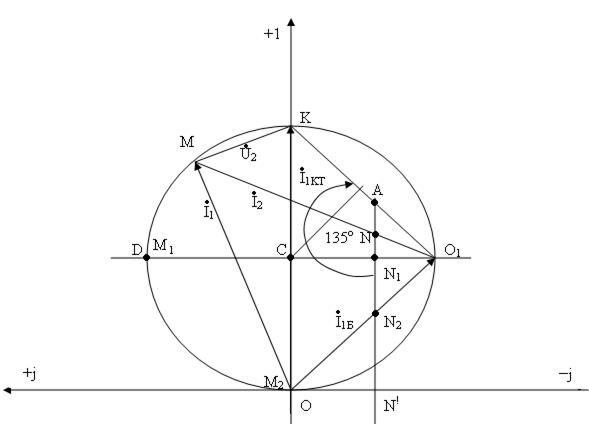
11.11 – сурет
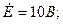
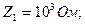
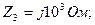
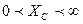 .
. 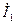 тоқтың шеңберлік диаграммасын құрып, сол бойынша
тоқтың шеңберлік диаграммасын құрып, сол бойынша 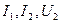 және
және 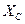 мәндерін екі ережеде
мәндерін екі ережеде 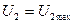 және
және 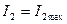 кезде белгілеу керек.
кезде белгілеу керек.

11.12 – сурет
Шешу: Шеңберді салу үшін шамаларды табамыз:
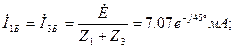
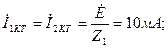
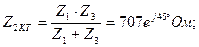
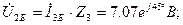
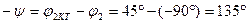
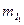 масштабты таңдап
масштабты таңдап 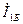 және
және 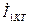 векторларды тұрғызамыз (11.11 – сурет).
векторларды тұрғызамыз (11.11 – сурет). 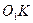 хорданы өткіземіз де,
хорданы өткіземіз де, 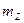 масштабты таңдап
масштабты таңдап 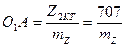 кесіндіні өткіземіз.
кесіндіні өткіземіз. 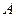 нүктесіден
нүктесіден 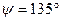 бұрышқа бұрып өзгертіп тұрған параметрдің
бұрышқа бұрып өзгертіп тұрған параметрдің 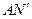 сызығын өткіземіз.
сызығын өткіземіз. 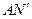 сызыққа
сызыққа 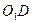 перпендикулярды түсіреміз және
перпендикулярды түсіреміз және 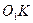 хорданың ортасына перпендикулярды өткізіп
хорданың ортасына перпендикулярды өткізіп 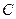 нүктені табамыз. Бұл нүкте диаграмманың ортасы болады.
нүктені табамыз. Бұл нүкте диаграмманың ортасы болады.
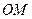 кесінді
кесінді 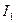 тоқты өлшейді,
тоқты өлшейді, 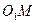 -кесінді
-кесінді 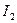 тоқты өлшейді,
тоқты өлшейді, 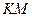 кесінді
кесінді 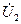 кернеуді өлшейді,
кернеуді өлшейді, 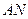 кесінді
кесінді 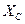 кедергіні өлшейді.
кедергіні өлшейді.
Масштабтар: 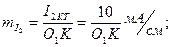
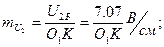
Мысал: 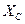 кедергіні
кедергіні 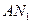 кесінді белгілейді.
кесінді белгілейді.
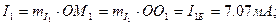
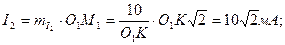
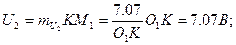
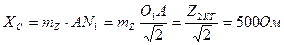
Он екінші тарау
12 Электр сүзгілер
12.1 Негізгі түсініктер және анықтамалар
Электрлік, радиотехникалық және телемеханикалық қондырғыларда және құрылғыларда жиі мынадай мәселе туады: жиіліктердің кең алқапты орынды алатын көп дабылдардан жиіліктердің енсіз алқабы бар бір немесе бірнеше дабылды бөліп шығару керек. Жиіліктердің былай бөлінуі электр сүзгілердің көмегімен орындалады.
Электр сүзгі – белгілі жиіліктердің алқабын шамалы сөнумен өткізетін, ал бұл жиілік алқаптың сыртындағы дабылдарды – күшті сөнумен өткізетін пассивтік төртұштық. Сөну шамалы алқап өткізу алқап деп аталады, басқа жиіліктер саласы – сөну алқап деп аталады.
Өткізу жиіліктер бойынша топтастыру:
1) Төменгі жиіліктердің сүзгілері – ТЖС, 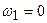 жиіліктен
жиіліктен 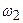 жиілікке дейін ауқымдағы дабылдарды өткізеді (12.1,а – сурет);
жиілікке дейін ауқымдағы дабылдарды өткізеді (12.1,а – сурет);
2) Жоғары жиіліктердің сүзгілері – ЖЖС, 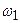 -ден
-ден 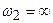 жиілікке дейін ауқымдағы дабылдарды өткізеді (12.1,б – сурет);
жиілікке дейін ауқымдағы дабылдарды өткізеді (12.1,б – сурет);
3) Жолақ алқапты өткізгіш сүзгілері – АӨС, 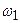 -ден
-ден 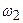 -ге дейін ауқымдағы дабылдарды өткізеді (12.1,в – сурет);
-ге дейін ауқымдағы дабылдарды өткізеді (12.1,в – сурет);
4) Бөгегіш сүзгілері – БС, 0-ден 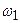 -ге дейін ауқымдағы дабылдарды және
-ге дейін ауқымдағы дабылдарды және 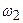 -ден
-ден 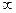 -ге дейін ауқымдағы дабылдарды өткізеді (12.1,г – сурет).
-ге дейін ауқымдағы дабылдарды өткізеді (12.1,г – сурет).
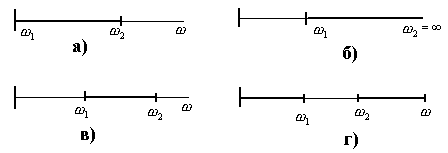
12.1 – сурет
Элементтердің қосылу әдісі бойынша топтастыру:
Сүзгілер Г-, П-, Т- және көпірлі сияқты элементтердің қосылуы болуы мүмкін және бірүзбелімен көпүзбелі болуы мүмкін.
Элементтердің түрлеріне тәуелді топтастыру:
a) реактивтік (L және С элементтерден құралады);
b) индукционды емес (R және С элементтерден құралады);
c) пьезоэлектрлік (кварц табақтардан құралады);
d) активтік RC-сүзгілер.
Жиілікті сипаттамаларының түрімен К және Т түрлі сүзгілерге бөлінеді.
12.2 – суретте төменгі жиілікті сүзгі төртұштық түрде бейнеленген.
Кіріс кернеу 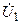 , шығыс кернеу
, шығыс кернеу 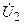 және жүктеменің кедергісі
және жүктеменің кедергісі 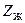 -ге тең.
-ге тең.
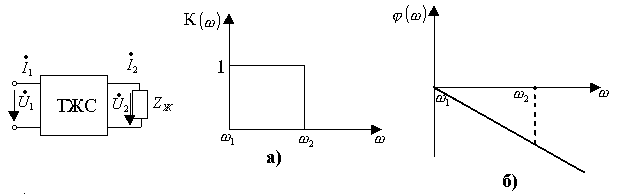
12.2 – сурет 12.3 – сурет
Комплексті беріліс коэффициент (кернеу бойынша).
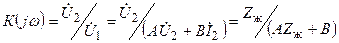 , (12.1)
, (12.1)
мұндағы А, В, Zж – жиіліктен тәуелді параметрлер.
Комплексті беріліс коэффициенті мына түрде келтіруге болады
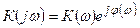 , (12.2)
, (12.2)
мұндағы 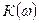 – амплитудалы жиілікті сипаттама (АЖС);
– амплитудалы жиілікті сипаттама (АЖС);
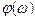 - фазалы-жиілікті сипаттама (ФЖС).
- фазалы-жиілікті сипаттама (ФЖС).
Өте оңды сүзгі үшін өткізу алқапта 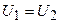 , яғни
, яғни 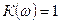 .
.
Келіскен жүктеме кезде комплексті беріліс коэффициент
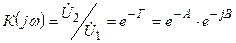 .
.
Өткізу алқапта сөну коэффициент А=0, фаза коэффициент В сызықты заң бойынша өзгереді (12.4, а,б – сурет).
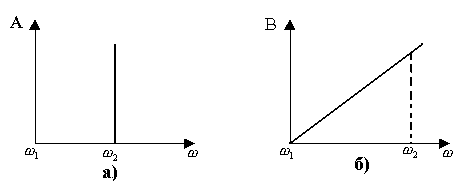
12.4 – сурет
Беріліс коэффициент Г=А+jB симметриялы төртұштықтың екіншілік параметрлеріне жатады, А – сөну (әлсірету) коэффициент [Hп], В – фаза коэффициенті [рад].
12.2 К түрлі сүзгілер:
a) төменгі жиіліктердің сүзгілері.
Симметриялы К түрлі сүзгілердің Т – немесе П – түрлі сүлбелері болады (12.5 – сурет) және оның 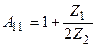 .
.
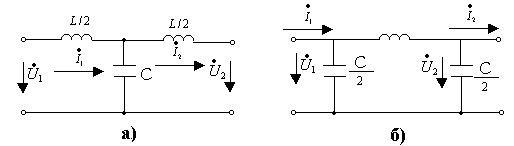
12.5 – сурет. К түрлі сүзгілер (а – Т-сияқты, б – П-сияқты)
Симметриялы төртұштықтар үшін 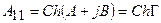 .
.
Сондықтан, Т-және П-сияқты сүзгілер үшін келіскен жүктеме кезде
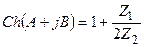 .
.
Төменгі жиілікті Т-және П-сияқты сүзгілерде (12.5, а,б – сурет)
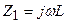 және
және 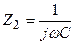 , яғни
, яғни
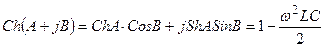 - нақтылы шама болғандықтан
- нақтылы шама болғандықтан
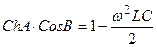 , ал
, ал 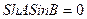 .
.
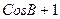 -ден – 1-ге дейін шектерде өзгереді, яғни төменгі шекаралық жиілік өткізу алқапта (А=0 кезде)
-ден – 1-ге дейін шектерде өзгереді, яғни төменгі шекаралық жиілік өткізу алқапта (А=0 кезде) 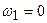 , жоғары шекаралық жиілік өткізу алқапта
, жоғары шекаралық жиілік өткізу алқапта
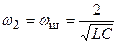 . (12.2)
. (12.2)
Симметриялы төртұштықтың сипаттамалы кедергісі 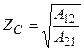 .
.
А12 және А21 мәндерін қойғаннан кейін Т-сияқты сүлбе үшін 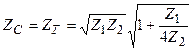 , ал П-сияқты сүлбе үшін
, ал П-сияқты сүлбе үшін 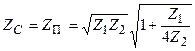 .
.
Дата добавления: 2017-01-29; просмотров: 1601;
