Эконометрических уравнений

Для простоты изложения материала будем считать, что системы содержат всего лишь два уравнения. При этом все полученные выводы могут быть обобщены на системы с произвольным числом уравнений и содержащихся в них переменных.

В эконометрике принято различать следующие виды систем уравнений:

- система независимых уравнений - когда каждая зависимая переменная Y рассматривается как функция одного и того же набора факторов-аргументов X:

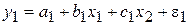
(7.1)

;

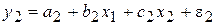- система рекурсивных уравнений - когда зависимая переменная Y одного уравнения представляет собой объясняющую переменную другого уравнения:

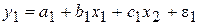
(7.2)

;

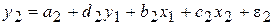- система внешне не связанных уравнений:

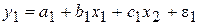
(7.3)

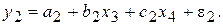
При этом Cov(e₁, e₂) ¹ 0. Данный вид модели может соответствовать экономической ситуации, когда уравнения (7.3) представляют зависимости результирующих экономических показателей различных предприятий, но действующих «в одной экономической среде» (например, компании «Газпром» и «ЛУКойл»). Внешне эти уравнения выглядят как не связанные друг с другом, однако в данной ситуации следует считать случайные отклонения e₁ и e₂ коррелированными. Отсюда следует, что эффективность оценивания можно повысить, рассматривая эти уравнения совместно;

- система взаимосвязанных (совместных) уравнений - когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую:

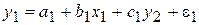
(7.4)

.

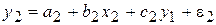Такая система уравнений называется структурной формой модели, а параметры a, b, c - структурными коэффициентами.

В общем случае системы эконометрических уравнений содержат множество взаимосвязанных переменных, которые принято классифицировать как экзогенные, эндогенные и предопределенные. Такая классификация осуществляется в зависимости от содержательной стороны модели и определяет разделение ролей в системе одновременных уравнений.

Эндогенными переменными называются взаимосвязанные переменные Y, которые формируются внутри модели (экономического объекта).

Экзогенными переменными называются внешние по отношению к модели переменные Х, значения которых определяются вне системы.

Предопределенными переменными (т. е. заранее определенными) называются экзогенные и лаговые эндогенные переменные системы.

Таким образом, эконометрическая модель в виде системы одновременных уравнений служит для объяснения поведения эндогенных переменных в зависимости от значений экзогенных и лаговых эндогенных переменных.

С точки зрения эконометрического анализа, основное отличие между экзогенными и эндогенными переменными заключается в том, что экзогенные переменные не коррелируют со случайными отклонениями (остатками) регрессии, а эндогенные, как правило, коррелируют.

Классическим примером систем одновременных взаимосвязанных уравнений является равновесная модель «спроса-предложения» в рыночной экономике:

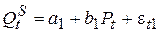(уравнение предложения)

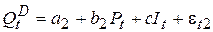(уравнение спроса) (7.5)

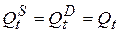(условие равновесия рынка),

где P_t - цена некоторого товара в момент времени t; I_t - доход в момент времени t; a, b, c - неизвестные коэффициенты (параметры модели), которые подлежат определению.

Модель содержит два регрессионных (поведенческих) уравнения и одно тождество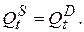

В соответствии с моделью (7.5) цена и величина спроса и предложения определяются одновременно, подчиняясь соответствующим уравнениям, т. е. формируют свои значения внутри модели. Поэтому обе эти переменные следует считать эндогенными. В отличие от них значения переменной I_t поступают в систему как характеристики внешней среды, т. е. формируются вне модели. Следовательно, доход является экзогенной переменной. Если с целью совершенствования модели в уравнение предложения ввести переменную P_{t - 1}, определяющую значения цены товара в предыдущий момент времени, то эта переменная и доход I_t будут являться предопределенными переменными в данной модели.