Виды условных уравнений в триангуляции при коррелатном способе уравнивания
Рассмотрим условные уравнения, возникающие при уравнивании углов триангуляции. При этом углы редуцированы на плоскость проекции Гаусса-Крюгера и исправлены за центрировку прибора и редукцию визирных целей.
8.1.1 Условие фигур. Сумма измеренных углов в замкнутой фигуре (например, в треугольнике) должна быть равна теоретической.
b*1 + b*2 + b*3 – 1800 = 0
vb1 + vb2 + vb3 + w = 0
w = b*1 + b*2 + b*3 – 1800
8.1.2 Условие суммы углов (условие станции). Условие возникает при измерении на станции углов между смежными направлениями и углов, являющихся суммой измеренных углов.
b*1 + b*2 - b*3 = 0
vb1 + vb2 - vb3 + w = 0
w = b*1 + b*2 - b*3
8.1.3 Условие горизонта. Возникает в случаях, когда на станции измерены углы с замыканием горизонта.
b*1 + b*2 + b*3 + b*4 + b*5 – 3600 = 0
vb1 + vb2 + vb3 + vb4 + vb5 + w = 0
w = b*1 + b*2 + b*3 + b*4 + b*5 – 3600
8.1.4 Условие полюса (боковое условие). Полюсное условие заключается в требовании, чтобы длина стороны, вычисленная двумя независимыми путями из решения треугольников сети, имела одно и тоже значение.
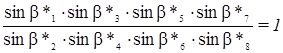
Примем, что Di = D lg sin bi – изменение lg sin bi при увеличении угла bi на 1”.
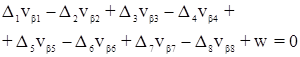
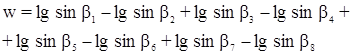
8.1.5 Условие исходных дирекционных углов (азимутальное условие). Условие возникает в сети, в которой две или более сторон сети имеют значения дирекционных углов, не подлежащие изменению при уравнивании.
aBD = aAC - b*1 + b*2 - b*3 + b*4 - b*5 + b*6
-vb 1 + vb 2 - vb 3 + vb 4 - vb 5 + vb 6 + w = 0
w = - b*1 + b*2 - b*3 + b*4 - b*5 + b*6 - (aBD - aAC)
При этом выбор ходовой линии не имеет значения. Частный случай:
vb 1 + vb 2 + vb 3 + w = 0
w = - b*1 + b*2 + b*3 - (aAC - aAB)
8.1.6 Условие базисов возникает в случаях, когда в сети имеется две или более сторон, длины которых не подлежат изменению в процессе уравнивания. Условие базиса заключается в требовании, чтобы длина одной исходной стороны, полученная от другой исходной стороны решением треугольников совпадала с заданным ее значением.
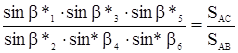
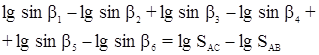
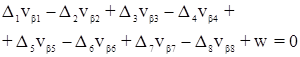
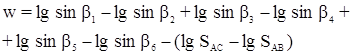
Частный случай:
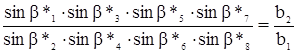
8.1.7 Условие координат возникает в том случае, если в сети имеется два и более разобщенных между собой исходных пункта с координатами, не подлежащими изменению при уравнивании. Для составления уравнений координат из сети выделяют простую и наиболее короткую цепь треугольников, соединяющих два исходных пункта.
,
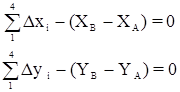где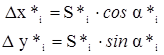 
- приращения координат по ходовой линии.
.
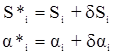С учетом малости поправок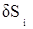 
и 
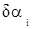можем записать:
,
,
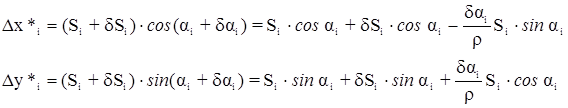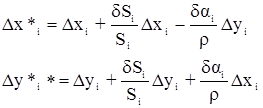где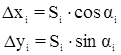 
- вычисленные приращения координат по неуравненным значениям Si и ai.
Произведем замену :
,
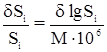где d lg Si – изменение lg Si, соответствующее поправке 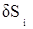и выраженное в единицах 6-го знака логарифма;
М = 0,43429 – lg e – модуль натуральных логарифмов.
Следовательно:
.
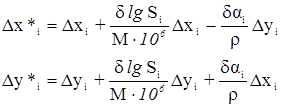Подставим эти уравнения в исходные условные уравнения и получим:
,
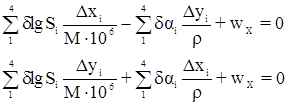где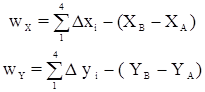 
- невязки в приращения координат.
Выразим длины и дирекционные углы ходовой линии через измеренные углы треугольников сети триангуляции:
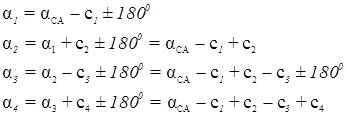
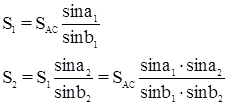
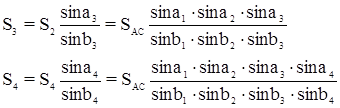
Из этого следует, что dai и dSi независимы, так как ai вычисляются через промежуточные углы ci, а стороны Si вычисляются при помощи связующих углов ai и bi. Независимость поправок dai и dSi существенно упрощает составление условных уравнений координат. Определим поправки:
da1 = – vc1
da2 = – vc1 + vc2
da3 = – vc1 + vc2 – vc3
da4 = – vc1 + vc2 – vc3 + vc4
d lg S1 = Da1 va1 - Db1 vb1
d lg S2 =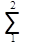 
{Dai vai - Dbi vbi}
d lg S3 =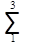 
{Dai vai - Dbi vbi}
d lg S4 =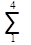 
{Dai vai - Dbi vbi}
Здесь Dai = d lg sin a1
Dbi = d lg sin b1
Подставляя dai и d lg Si в условные уравнения получим в окончательном виде:
уравнение абсцисс:
(XB - XA)·{Da1 va1 - Db1 vb1} + k·(YB - YA)·vc1 +
+ (XB - XA)·{Da2 va2 - Db2 vb2} + k·(YB - YA)·vc2 +
+ (XB - XA)·{Da3 va3 - Db3 vb3} + k·(YB - YA)·vc3 +
+ (XB - XA)·{Da4 va4 - Db4 vb4} + k·(YB - YA)·vc4 +
+ 434,29·wX = 0
уравнение ординат
(YB - YA)·{Da1 va1 - Db1 vb1} + k·(XB - XA)·vc1 +
+ (YB - YA)·{Da2 va2 - Db2 vb2} + k·(XB - XA)·vc2 +
+ (YB - YA)·{Da3 va3 - Db3 vb3} + k·(XB - XA)·vc3 +
+ (YB - YA)·{Da4 va4 - Db4 vb4} + k·(XB - XA)·vc4 +
+ 434,29·wY = 0
где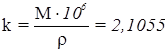 
;
vai, vbi, vci – поправки в измеренные углы;
xi, yi – приближенные координаты в км;
Dai, Dbi – изменения lg sin ai и lg sin bi, выраженные в шестом знаке lg;
M = 0,43429;
r = 206265”.
Дата добавления: 2016-06-02; просмотров: 3199;