Сущность двухгруппового коррелатного способа уравнивания (способ Крюгера)

Пусть имеется система k = r + m условных уравнений:

A V + W = 0,

.

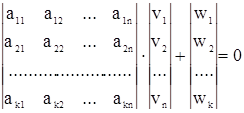Разобьем ее на две группы:

.

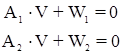В первой группе r условных уравнений, а во второй – т уравнений.

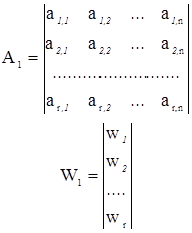
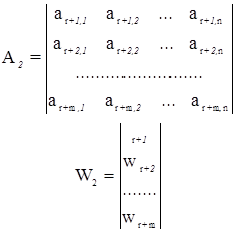
Как правило, в триангуляции имеем равноточные измерения, т.е. P = Е = Q. Рассмотрим уравнивание при равноточных угловых измерениях. По условным уравнениям 1-й группы составляют систему нормальных уравнений:

(A₁ A₁^T) K₁ + W₁ = 0.

Решив эту систему К₁ = - (А₁ А₁^Т)^-1 W₁ вычисляют первичные поправки в измеренные углы V₁ = A₁^T K₁.

Вторую группу условных уравнений A₂ V + W₂ = 0 необходимо преобразовать к виду A₂’ V₂ + W₂’ = 0, коэффициенты которой определяются по формулам:

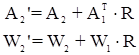т.е.

,

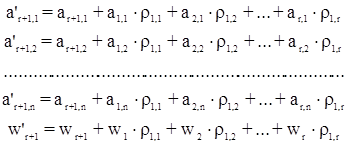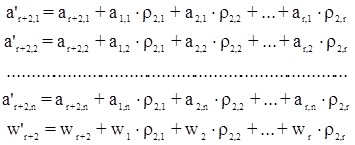
и т.д.

Для получения преобразованных коэффициентов и свободных членов условных уравнений 2-й группы необходимо вычислить т групп вспомогательных коэффициентов r_i,k. Для этого необходимо решить т систем уравнений, отличающихся между собой только свободными членами:

(A₁ A₁^T)·R + A₁ A₂^T = 0,

R = - (A₁ A₁^T)^-1 · (A₁ A₂^T).

Решая систему нормальных уравнений, соответствующую преобразованной системе условных уравнений 2-й группы A₂’ · (A₂’)^T · K₂ + W₂’ = 0 получают коррелаты:

K₂ = - (A₂’ (A₂’)^T)^-1 · W₂’.

Вторичные поправки в измеренные углы вычисляют по формуле:

V₂ = (A₂’)^T · K₂.

Полная поправка в измеренные углы вычисляется по формуле:

V = V₁ + V₂.

Для оценки точности вычисляются V^TV = V₁^TV₁ + V₂^TV₂,

где V₁^TV₁ = - K₁^T W₁ = - W₁^T K₁,

V₂^TV₂ = - K₂^T W₂ = - W₂^T K₂.

Далее оценка точности выполняется по известным формулам:

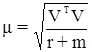и

,

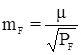где r + m – число избыточных измерений или число условных уравнений 1-й и 2-й групп;

P_F – вес функции.