Уравнивание сетей триангуляции по направлениям

При непосредственном измерении направлений уравнивание сетей триангуляции должно выполнятся по направлениям.

Угол является разностью двух направлений. Поэтому для получения условного уравнения при уравнивании направлений необходимо в условных уравнениях для углов заменить поправки в углы разностью поправок направлений и выполнить приведение подобных членов.

Например, для условного уравнения фигуры имеем:

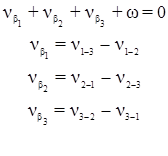
Следовательно:

v_1-3 – v_1-2 + v_2-1 – v_2-3 + v_3-2 – v_3-1 + w = 0.

Сумма коэффициентов при поправках направлений всегда будет равна нулю. При уравнивании направлений в сети не могут возникать условные уравнения горизонта и сумм углов, т.к. каждое направление и его поправка будет участвовать в вычислении двух соседних углов один раз со знаком «+», а второй раз – со знаком «–».

В свободной сети, состоящей из N наблюдаемых объектов, число всех условных уравнений будет равно:

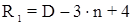
Где D – число измеренных направлений в сети.

Сюда входят уравнения фигур и полюсов. В несвободной сети общее число условных уравнений равно:

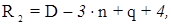
где q – число избыточных уравнений и определяется по формуле:

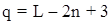
где L – число всех линий в сети.

Число уравнений фигур.

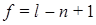
где l – число сплошных линий в сети

п – пунктов в сети.

При уравнении по направлениям применение группового уравнивания уже не дает такого эффекта, как при уравнивании углов, т.к. уравнения фигур содержат общие поправки направлений и не являются независимыми.

В настоящее время групповое уравнивание по направлениям в геодезической и маркшейдерской практике не применяется.

9 УРАВНИВАНИЕ СЕТЕЙ ТРИАНГУЛЯЦИИ ПАРАМЕТИЧЕСКИМ СПОСОБОМ

Постановка задачи

Обозначим измеряемые в сети триангуляции величины через М₁, М₂, …, М_п, а их измеренные значения M’₁, M’₂, …, M’_n. Уравненные значения измеряемых величин вычисляются по формулам:

M*_i = M’_i + v_i,

где v_i – поправки к результатам измерений, полученные при уравнивании.

Необходимые неизвестные параметры сети обозначим через x, y, u, …, z, а их приближенные значения – x’, y’, u’, …, z’. Уравненные значения параметров вычисляются по формулам:

.

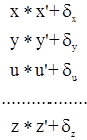Необходимые неизвестные параметры связаны с измеряемыми величинами функциональными зависимостями:

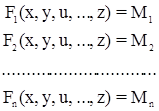
При этом количество параметров в сети составляет r, а количество измеренных величин – п (причем n > r). Задача уравнивания сводится к определению поправок в предварительные значения параметров d_x, d_y, d_n, …, d_z при условии [pvv] = min, где р – веса результатов измерений.

Затем вычисляются поправки к результатам измерений v_i (i = 1, n), уравненные значения неизвестных x*, y*, u*, …, z* и измеряемых величин M*_i, а также оценивается точность измерений и уравненных величин.

9.2 Сущность уравнивания

На основании введенных обозначений запишем уравнения связи между уравненными значениями параметров и измеряемых величин:

F_i (x*, y*, u*, …, z*) = M*_i или

F_i (x’+d_x, y’+d_y, u’+d_u, …, z’+d_z) = M’_i + v_i.

При корректном определении предварительных значений параметров x’, y’, u’, …, z’ поправки к ним d_x, d_y, d_n, …, d_z представляют собой сравнительно небольшие величины. Поэтому при разложении функции F_i в ряд можно ограничится членами первого порядка:

.

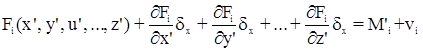Введем обозначения:

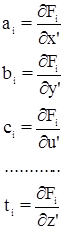
l_i = F_i (x’, y’, u’, …, z’) – M’_i

и после преобразований получим параметрические уравнения поправок в линейном виде:

a_i d_x + b_i d_y + c_i d_u + … + t_i d_z + l_i = v_i с весом p_i.

Следовательно, система параметрических уравнений поправок имеет вид:

.

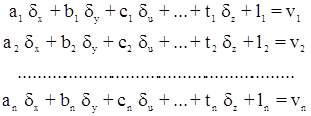Решение этой системы параметрических уравнений поправок при условии [pvv] = min приводит к системе с r нормальных уравнений с r неизвестными:

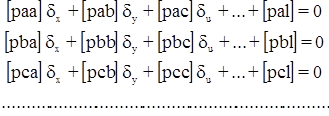
В результате решения системы нормальных уравнений получают поправки к приближенным значениям параметров и их уравненные значения. Затем по формуле:

v_i = a_i d_x + b_i d_y + c_i d_u + … + t_i d_z + l_i

определяют поправки к результатам измерений M_i и уравненные значения измеренных величин M*_i. Контроль уравнительных вычислений осуществляется по формулам:

[pll] – [pvv] = -[pal] d_x – [pbl] d_y – … –[ptl] d_z,

[pav] = [pbv] = [pcv] = … = [ptv] = 0.

Окончательный контроль выполняется определением уравненных значений измеряемых величин по формулам:

M*_i = F_i (x*, y*, u*, …, z*)

M*_i = M’_i + v_i.

Для оценки точности вычисляют:

· среднюю квадратическую погрешность единицы веса:

,

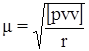где r – число избыточных измерений;

· среднюю квадратическую погрешность измеренной величины:

,

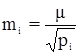где р_i – вес измеренной величины;

· среднюю квадратическую погрешность любой функции параметров j (x, y, u, …, z):

,

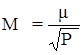где P_j - вес функции j, вычисляемый при уравнивании.

9.3 Сведения об эквивалентных уравнениях погрешностей

Две системы уравнений погрешностей называются эквивалентными, если им соответствует одна и та же система нормальных уравнений, а следовательно, одни и те же значения неизвестных величин. При уравнительных вычислениях иногда можно их существенно упростить путем использования эквивалентной системы параметрических уравнений поправок.

В связи с тем, что при использовании способа круговых приемов при угловых измерениях в триангуляции непосредственно измеряются направления, а не углы, уравнивание триангуляции должно выполняться по измеренным направлениям.

Предположим, что на пункте k измерены т направлений M_k-1, M_k-2, …, M_k-m на смежные пункты 1, 2, …, т.

РИС