аналитических сетей

Аналитические сети строятся в виде отдельных треугольников, центральных систем, четырёхугольников, цепей треугольников между сторонами или пунктами опорной сети высшего класса. К аналитическим сетям относят также сети, в которых положение пунктов определяется прямой, обратной, комбинированной засечками.

Сущность прямой засечки ( рисунок 8 ) заключается в измерении горизонтальных углов ( a и b ) на пунктах, например, А иВ с известными координатами Х_А, У_А; Х_В,У_Ви вычислении координатХ_Р, У_Р определяемого пункта Рпо формулам Юнга

Х_Р = ( Х_А сtg a+ Х_B сtg b + У_В – У_А ) / ( сtg a+ сtg b ),

У_Р = ( У_А сtg a+ У_B сtg b + Х_В – Х_А ) / ( сtg a+ сtg b).

Р

С

b^/

a b a^/

А

B

Рисунок 8 - Определение координат пункта прямой засечкой

Для контроля определяют координаты пункта из второго треугольника и вычисляют средние значения координат.

Сущность обратной засечки( рисунок 9 )заключается в измерении горизонтальных углов a, b, gна определяемом пункте Р. Затем по координатам исходных пунктов А, В, Сиизмеренным углам вычисляют дирекционныеуглы a_АР стороныАР, a_ВР стороны ВР,а затем координаты Х_Р, У_Ропределяемого пункта по нижеприводимым формулам

D A

Р

G a

b

C B

Рисунок 9 - Сущность обратной засечки

[(Х_В -Х_А) ctg a+(Х_A- Х_С) ctg b+У_В -У_С]

сtg a_АР = ,

[(У_В -У_А) ctg a+(У_А- У_С) ctg b+Х_С -Х_В]

a_ВР = a_АР + a,

У_Р = [У_В + ( У_В -У_А) ctg a_АР + Х_А - Х_В] / (сtg a_{ВР -} сtg a_AР),

X_P = X_A + (У_P - У_А) ctg a_AР.

Для контроля измеряют третий угол g между пунктами А и D и определяют координаты пункта Р с учётом координат пункта D.

Определение координат определяемого пункта Р комбинированной засечкой заключается в измерении угла на одном из исходных пунктов, например, угла a₁ на пункте А, и угла g₁ на определяемом пункте Р ( рис.10 ). Для контроля измеряют аналогичные углы на пунктах Си Р.

Р

g₂

g₁ a₁ С

a₁ b ₁ b ₂

А

В

Рисунок 10 - Определение координат пункта комбинированной

засечкой

Прямоугольные координаты определяемого пункта вычисляют по формулам Юнгас контролем из двух треугольников

б) Создание съёмочного обоснования проложением

Теодолитных ходов

Ходы съёмочного обоснования, развиваемые методом полигонометрии, называют теодолитными ходами.

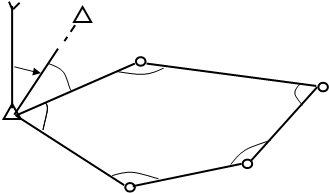
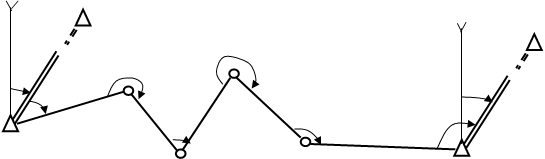
Теодолитные ходы опираются на пункты ГГС или пункты сетей сгущения ( местного значения ). По своей форме они бывают замкнутыми, опирающимися на один пункт сети ( рисунок 11 ) или разомкнутыми ( рисунок 12 ), опирающимися минимум на два пункта сети.

В

a ₀ 1

d₀ d ₁ 2

b₀ b₁ b₂

b_А

А b₃ d₂

d₄

b₄ d₃ 3

Рисунок 11 - Замкнутый теодолитный ход

В

D

a_Н b₃

b₁ a_К

b_А 1 3

d₁ d₂ b₂ d₃ d₄ b₄ b_C

А d₅

2 4С

Рисунок 12 - Разомкнутый теодолитный ход

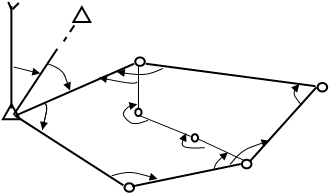
При проложении замкнутых теодолитных ходов с целью контроля внутри него прокладывают, как правило, диагональный ход, опирающийся на пункты замкнутого хода, например, пункты 2, 4 ( рисунок 13 ).

В

a₀ 4

b₀ 3

А 6

Рисунок 13 - Замкнутый и диагональный теодолитные ходы

При создании съёмочного обоснования из проложения теодолитных ходов соблюдается следующая последовательность работ:

- проектирование ходов по планам и картам;

- рекогносцировка ходов с целью уточнения составленного проекта и окончательное установление местоположения пунктов хода;

- измерение углов поворота полным приёмов теодолитом 30^" точности ( Т30, 2Т30П );

- измерение длин линий землемерной лентой в прямом и обратном направлениях или дважды в одном направлении.

В измеренную линию вводят поправки за компарирование, температуру, если температура компарирования и температура при измерениях различаются более чем на 8⁰, за приведение длины линии к горизонту, если наклон линии к горизонту превышает 1.5⁰.

Результаты измерений записывают в журнал теодолитного хода.

По окончании полевых измерений производится камеральная обработка, конечной целью которой является определение уравненных значений прямоугольных координат пунктов.

Камеральная обработка измерений, выполненных при проложении теодолитного хода, производят в следующем порядке:

- проверяют вычисления углов и расстояний в полевых журналах и вычислений по введению поправок в длины линий; составляют схемы проложенных теодолитных ходов;

- вычисляют суммы измеренных углов S b^/ _i

S b^/ _i = b₁ + b₂ +b₃ ...+ b_n;

- вычисление теоретической суммы измеренных углов S b_Т

S b_Т = 180⁰(n-2),

где n – число измеренных углов в ходе,

если проложен замкнутый ход, и по формулам

S b_Т = a_к - a_н + 180⁰ n,

S b_Т = a_н - a _к + 180⁰ n,

если измерены соответственно левые и правые по ходу углы в разомкнутых ходах;

- вычисляют угловую невязку хода f _b

f_b= S b_Т - S b_Т^'_i ;

-вычисляют допустимую невязку ходаf _{b доп}

f_{b доп} < 3tÖ n,

где t – точность теодолита ( 30^" );

- вычисляют поправки в измеренные углы d_{b i}

d _{b i} = - f _b / n;

- вычисляют уравненные ( исправленные ) горизонтальные углы b _i

b_i = b^'_i + d_{b i};

- контролируют правильность вычислений

S b _i = S b _Т.

- вычисляют дирекционные углы направлений a _i

a_{i =} a _i-1 ± 180⁰ + b _i ,

a_{i =} a _i-1 ± 180⁰ - b _i ,

если измерены соответственно левые и правые по ходу углы,

- вычисляют приближённые приращенийя координат DХ^'_i, DУ^'_i

DХ^'_i = d cos a_i,

DУ^'_i = d sin a_i;

- вычисляют суммы приближённых значений приращений координатS DХ^'_i , S DУ^'_i

S DХ^'_i = DХ₁ + DХ₂ + DХ₃ +...+ DХ_n,

S DУ^'_i = DУ₁ + DУ₂ + DУ₃ +...+ DУ_n;

- вычисляют теоретические разности приращений координат

S DХ_Т = Х_К - Х_Н,

S DУ_Т = У_К - У_Н;

_- вычисляют линейные невязки по абсциссе f_xи по ординатеf_y

f_x = S DХ_Т - S DХ^'_i,

f_у = S DУ_Т - S DУ^'_i;

Невязки по абсциссе и ординате свидетельствуют об отклонения конечной точки хода от действительного положения. В этом случае необходимо оценить точность хода. Для этого вычисляют линейную невязку хода DР

DР² = f_Х² + f_У²,

а затем относительную невязку хода

DР / Р = (f_Х² + f_У²)² / Р,

которая не должна превышать 1:2000для замкнутого хода и 1:1000 – для диагонального ( разомкнутого );

- вычисляют поправки d_Хi, d_Уiв приближённые значения приращений координат

d_Хi = - f_Х d_i / P,

d _Уi = - f_У d_i / P;

_- вычисляют уравненные ( исправленные поправками)приращения координат DХ_i, DУ_i

DХ_i = DХ^'_i + d_Хi,

DУ_i = DУ^'_i + d_Уi;

- контролируют правильность вычисления уравненных приращений координат

S DХ _i = S DХ_Т,

S DУ_i = S DУ_Т;

- вычисляют уравненные значения прямоугольных координат пунктов съёмочной сети

Х_i = Х_i-1 + DХ _i,

У_i = У_i-1 + DУ_i.