Уравнивание сетей триангуляции

При уравнивании триангуляции по углам могут возникнуть семь типов условных уравнений:

1. условие фигур;

2. условие суммы углов;

3. условие горизонта;

4. условие полюса;

5. условие твердых дирекционных углов;

6. условие базисов;

7. условие координат.

Совместное решение условных уравнений методом наименьших квадратов является общим, но не самым простым приемом решения задачи. При совместном решении условных уравнений необходимо решить систему нормальных уравнений в сети.

Например, при уравнивании углов в цепочке из 10 треугольников, опирающихся на две пары исходных пунктов будем иметь:

1. 10 условных уравнений фигур;

2. 2 условных уравнения координат;

3. 1 условное базисное уравнение;

4. 1 условное азимутальное уравнение.

Т.е. будем иметь систему нормальных уравнений 14 порядка.

Упрощение процедуры уравнивания достигается применением группового уравнивания. При уравнивании триангуляции наибольшее применение находит двухгрупповой способ.

В общем случае двухгрупповой способ уравнивания не проще совместного решения всех условных уравнений. Но в частных случаях удается существенно сократить вычисления. Наибольший эффект получается при включении в первую группу только условных уравнений фигур с коэффициентами, равными единице. В этом случае решение условных уравнений 1-й группы сводится к распределению невязки каждого уравнения поровну на все входящие в него углы. Упрощаются и все остальные вычисления.

Система условных уравнений поправок

A V + W = 0

преобразуется в систему нормальных уравнений:

(A Q A^T) K + W = 0

где А – матрица коэффициентов условных уравнений, состоящая из п столбцов и k строк;

п – число измеренных углов;

k – число условных уравнений;

Q = P^-1 – обратная весовая матрица (при равноточных измерениях углов Q = E и ее можно не учитывать, т.е. A Q A^T = А А^Т);

W – вектор невязок в условных уравнениях.

При решении нормальных уравнений вычисляются коррелаты:

K = - (A Q A^T)^-1 W.

Поправки в измеренные углы вычисляются по формуле:

V = Q K A^T.

По вычисленным уравненным углам х* = х + v окончательно решаются треугольники и вычисляются уравненные координаты всех определяемых пунктов сети триангуляции. Средняя квадратическая погрешность единицы веса вычисляется по формуле:

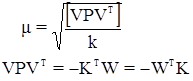
а средняя квадратическая погрешность функции F по формуле:

.