Составление уравнений погрешностей
Вывод уравнений погрешностей при уравнивании триангуляции по направлениям сводится к установлению зависимости между поправками координат и поправками измеренных направлений. Ранее после дифференцирования уравнения
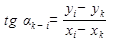
получено уравнение
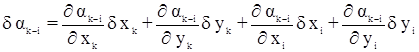 .
.
Дифференцируя исходное уравнений tg a = f (x, y) получим:
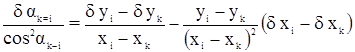 .
.
Учитывая, что xi – xk = Sk-i · cos ak-i
yi – yk = Sk-i · sin ak-i
где Sk-i – длина стороны между пунктами i-k находим
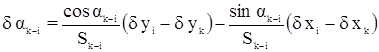
Для получения d ak-i в секундах необходимо правую часть уравнения умножить на r”. Если Sk-i выражено в километрах, то для получения d x и d y в дециметрах в уравнении
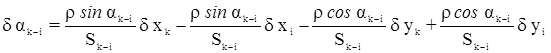
принимаем r = 20,6265”.
Тогда обозначая
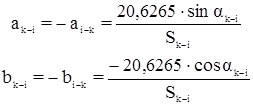
получим уравнение:
d ak-i = ak-i d xk + bk-i d yk – ak-i d xi – bk-i d yi.
В этом уравнении пункты k и i являются определяемыми. Т.к. поправки в исходные координаты не вводятся, то если пункт і является исходным, то:
d ak-i = ak-i d xk + bk-i d yk .
Если оба пункта являются исходными, то d ak-i = 0.
Таким образом, мы получили так называемые непреобразованные уравнения погрешностей, в которых неизвестными являются поправки d x и d y к приближенным значениям координат x’ и y’ определяемых пунктов и ориентирные поправки d z:
1. измеренному направлению с исходного пункта k на исходный пункт i соответствует уравнение:
- d zk + lk-i = vk-i.
2. измеренному направлению с определяемого пункта k на исходный пункт i соответствует уравнение:
- d zk + ak-i d xk + bk-i d yk + lk-i = vk-i.
Направлению с исходного пункта i на определяемый пункт k соответствует уравнение:
- d zk + ak-i d xk + bk-i d yk + li-k = vi-k.
3. измеренному направлению с определяемого пункта k на определяемый пункт i соответствует уравнение:
- d zk + ak-i d xk + bk-i d yk – ak-i d xi – bk-i d yi + lk-i = vk-i.
Веса всех преобразованных уравнений погрешностей равны между собой, т.е. направления измерены равноточно. Число уравнений погрешностей равно общему числу измеренных направлений, включая и направления между исходными пунктами. Число неизвестных равно 2 р + q, где р – количество определяемых пунктов; q – количество отнаблюденных пунктов, равное числу поправок d z.
При уравнивании триангуляции по углам уравнения погрешностей получают как разности из уравнений для соответствующих направлений. Например, в пункте k между направлениями на пункты i и j имеем уравнения погрешностей для направлений:
- d zk + ak-i d xk + bk-i d yk – ak-i d xi – bk-i d yi + lk-i = vk-i
- d zk + ak-j d xk + bk-j d yk – ak-j d xj – bk-j d yj + lk-j = vk-j.
Для угла bk = ak-j - ak-i получим:
(ak-i – ak-j) d xk + (bk-i – bk-j) d yk – ak-j d xj – bk-j d yj + ak-i d xi – bk-i d yi + lb = vb.,
где lb = lk-j – lk-i = (a’k-j - a’k-i) - bk.
При этом число уравнений погрешностей равно числу измеренных углов, а число неизвестных – удвоенному числу определяемых пунктов.
9.5 Преобразование уравнений погрешностей
Для упрощения вычислений непреобразованные уравнений погрешностей (т.е. уравнения с ориентирными поправками dz) преобразовывают на основании теории эквивалентных уравнений. Эти преобразования позволяют сократить число уравнений погрешностей и число входящих в них неизвестных.
9.5.1 Исключение ориентирных поправок.
Вес измеренного направления (непреобразованного уравнения погрешностей) примем равным ½. Для каждого наблюдаемого пункта записывают группу уравнений с общеориентирной поправкой dz.
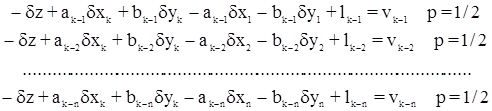
Если один или несколько пунктов являются исходными, то поправки в координаты этих пунктов равны нулю. На основании 1-го правила Шрейбера исключаем ориентирную поправку dz из п уравнений, заменив ее эквивалентной системой п+1 уравнений:
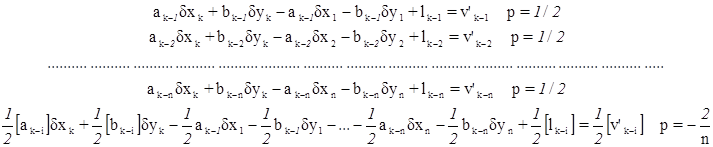
В этой системе уравнений поправки v’k-i уже не являются поправками к измеренным направлениям, а численно равны v’k-i = vk-i + dzk. Учитывая, что
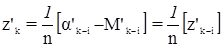
и [lk-i] = 0, на основании третьего положения теории эквивалентных уравнений последнее суммарное уравнение заменим на уравнение
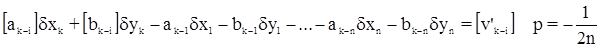
Аналогично преобразовывают уравнения погрешностей на остальных наблюдаемых пунктах.
9.5.2 Сложение уравнений взаимных направлений.
Для стороны сети триангуляции между определяемыми пунктами k и i в случае двустороннего визирования после исключения ориентирных поправок получим два уравнения, которые отличаются только свободными членами:
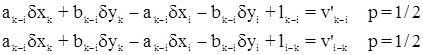
На основании второго положения теории эквивалентных уравнений эти уравнения могут быть заменены одним уравнением:
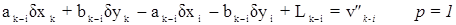
где 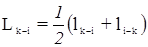 .
.
9.5.3 Приведение уравнений погрешностей к весу, равному 1.
Теперь только уравнения для сторон с односторонним визированием и суммарные уравнения будут иметь веса, не равные 1. Их можно привести к весам, равным 1 или –1. Согласно третьему положению теории эквивалентных уравнений такие уравнения можно заменить на эквивалентные с весом 1 или –1.
a dx + b dy + … + l = v с весом р
на
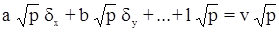 с весом р = 1.
с весом р = 1.
9.6 Составление преобразованных уравнений погрешностей
На основании правил составления эквивалентных уравнений погрешностей можно сформулировать правила составления преобразованных уравнений погрешностей:
1-е правило. Стороне сети между определяемыми пунктами k и i соответствует уравнение погрешностей:
а) в случае двустороннего визирования:
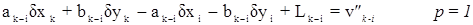
б) в случае одностороннего визирования с пункта k на пункт i:
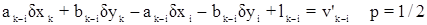 .
.
2-е правило.Стороне сети между определяемым пунктом k и исходным пунктом i соответствует уравнение погрешностей:
а) в случае двустороннего визирования:
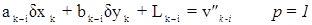
б) в случае одностороннего визирования с пункта k на пункт i:
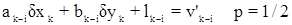 .
.
3-е правило. Каждому отнаблюденному пункту k отвечает суммарное уравнение с отрицательным весом:
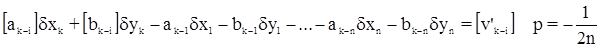
При этом на исходном пункте k в суммарных уравнениях отсутствуют два первых слагаемых с коэффициентами [ak-i] и [bk-i].
Общее число уравнений погрешностей равно числу сторон в сети (не считая сторон между исходными пунктами) плюс общее число отнаблюденных пунктов. В преобразованных уравнениях погрешностей неизвестными являются поправки в координаты определяемых пунктов. Количество неизвестных равно удвоенному числу определяемых пунктов.
9.7 Последовательность и контроль уравнительных вычислений
Этапы уравнивания:
1. подготовка исходных данных (Хисх, Yисх, aисх);
2. вычисление предварительных координат определяемых пунктов Х’опр, Y’опр;
3. вычисление предварительных дирекционных углов a’k-i и длин сторон Sk-i;
4. составление уравнений погрешностей;
5. составление и решение нормальных уравнений;
6. вычисление уравненных значений:
координат:
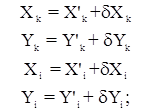
дирекционных углов:
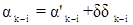 ,
,
где dak-I = ak-i dxk + bk-i dyk – ak-i dxi – bk-i dyi (k, i - определяемые);
dak-I = ak-i dxk + bk-i dyk (k - определяемый, i - исходный);
dak-I = 0 (k, i - исходные);
и направлений:
Mk-i = M’k-i + vk-i,
где vk-i = - dzk + dak-i + lk-i;
dzk = 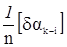 .
.
7. выполнение контрольных вычислений. Кроме того, для контроля ak-i вычисляют по уравненным координатам точек:
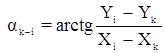 .
.
Далее вычисляют [vk-i] для каждого пункта, т.к. [vk-i] должно быть рано 0.
8. оценка точности уравненных элементов сети. При весе измеренных направлений р = ½ средняя квадратическая погрешность единицы веса равна:
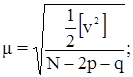
где N – число измеренных направлений (включая и между исходными пунктами);
р – число определяемых пунктов;
q – число отнаблюденных пунктов.
СКП измеренного направления:
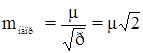 .
.
СКП измеренного угла:
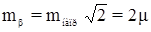 .
.
СКП положения пункта:
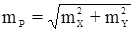 ,
,
где 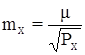 ;
;
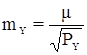 .
.
Дата добавления: 2016-06-02; просмотров: 1816;
