Из рисунка видно, что
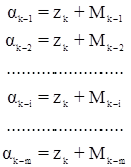
где ak-i – дирекционный угол стороны сети с пункта k на пункт i;
Mk-i – измеренное направление k-i;
zk – дирекционный угол начального направления.
Введем обозначения уравненных значений ak-i, Mk-i и zk.
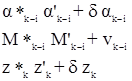 ,
,
где a’k-i и d ak-i – приближенное значение дирекционного угла стороны сети триангуляции k-i и поправка к нему;
M’k-i и vk-i – измеренное значение направления k-i и поправка к нему;
zk и d zk – приближенное значение ориентирного угла zk и поправка к нему.
Следовательно, для произвольного направления (т.е. для стороны k-i) можем записать уравнение в виде:
a*k-i = z*k + M*k-i
или
a’k-i +d ak-i = z’k + d zk + Mk-i + vk-i
или
– d zk +d ak-i +{(a’k-i – M’k-i) – z’k } = vk-i.
Обозначим lk-i = (a’k-i – M’k-i) – z’k = z’k-i – z’k,
где z’k-i = a’k-i – M’k-i – приближенное значение ориентирного угла стороны k-i.
Тогда уравнение поправок для произвольного направления принимает вид:
– d zk + d ak-i + lk-i = vk-i
На наблюдательном пункте k будем иметь систему уравнений поправок:
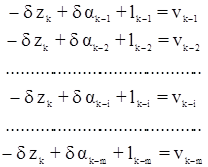 .
.
Учитывая зависимость дирекционного угла стороны от координат конечных точек:
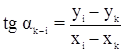
после дифференцирования получим уравнение:
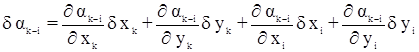
или с учетом ранее принятых обозначений:
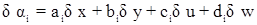
Таким образом, на станции будем иметь систему параметрических уравнений поправок:
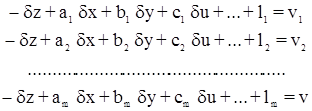
Т.е. кроме необходимых неизвестных координат определяемых точек при уравнивании триангуляции по направлениям будем иметь еще неизвестные ориентирные углы. Для их исключения используется теория эквивалентных уравнений.
Первое положение (первое правило Шрейбера).
Система т уравнений погрешностей с r+1 неизвестными:
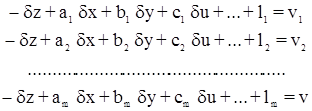
может быть заменена системой т + 1 уравнений погрешностей с r неизвестными:
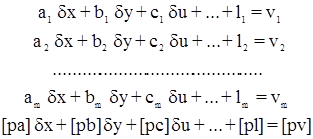
Обязательное условие – при одном из неизвестных (dz) во всех т уравнениях постоянный коэффициент (в нашем случае –1). Составим систему нормальных уравнений по исходной системе уравнений поправок:
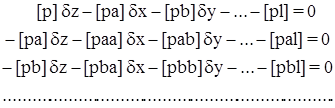
После исключения неизвестного dz переходим к системе:
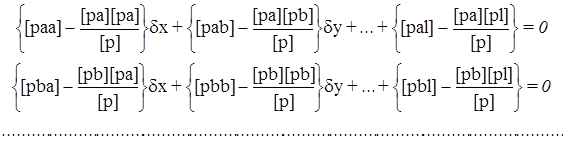 .
.
Если составить нормальные уравнения по второй системе, то они будут тождественны полученным, т.е. 1-я и 2-я системы параметрических уравнений поправок эквивалентны.
Второе положение (второе правило Шрейбера).
Система т уравнений погрешностей, отличающихся между собой только свободными членами и весами
a dx + b dy + … + l1 = v1 с весом р1
a dx + b dy + … + l2 = v2 с весом р2
.............................................................
a dx + b dy + … + lт = vт с весом рт
может быть заменена одним уравнением:
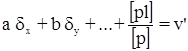 с весом [p].
с весом [p].
Доказывается аналогично.
Третье положение (третье правило Шрейбера).
Уравнение погрешностей
a dx + b dy + … + l = v с весом р
может быть заменено уравнением
q a dx + q b dy + … + q l = q v с весом 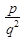 .
.
Это положение используется для приведения уравнений погрешностей к весу, равному единице. Если 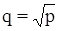 , то получим:
, то получим:
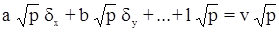 с весом р = 1.
с весом р = 1.
Дата добавления: 2016-06-02; просмотров: 1039;
