Уравнивании триангуляции
При уравнивании сетей триангуляции в первую группу включают независимые условные уравнения фигур с коэффициентами, равными единице. например, в цепочке триангуляции составляются следующие уравнения фигур:
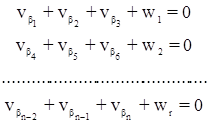 .
.
Этим условным уравнениям 1-й группы соответствуют нормальные уравнения:
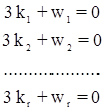 .
.
Следовательно,
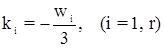
и первичные поправки будут равны:
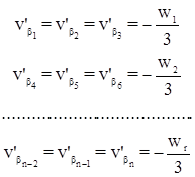
Уравнения второй группы, как правило, составляют по углам, исправленным первичными поправками. В этом случае сразу вычисляются значения преобразованных невязок. Преобразование коэффициентов условных уравнений 2-й группы выполняют следующим образом:
1. подсчитывают сумму коэффициентов условного уравнения второй группы по каждому треугольнику. Например, для первого уравнения и первого треугольника будет:
[a] = ar+1, 1 + ar+1, 2 + ar+1, 3;
2. вычисляют преобразованные коэффициенты:
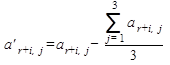
где i – номер уравнения;
j – номер угла в треугольнике.
3. контролируют вычисление преобразованных коэффициентов:
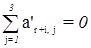
В связи с тем, что сумма преобразованных коэффициентов условных уравнений второй группы равна нулю, то и сумма вторичных поправок по каждому треугольнику будет равна нулю. Т.е. введение вторичных поправок не нарушает уже выполненное решение уравнений фигур.
Затем вычисляются уравненные значения измеренных углов и окончательные (т.е. уравненные) значения координат определяемых пунктов. Оценка точности выполняется по известным формулам:
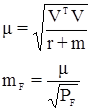 .
.
Дата добавления: 2016-06-02; просмотров: 1008;
