Измерения углов в триангуляции

Даны невязки в треугольниках

w₁ , w₂ , . . . , w_n ,

причем

(2.52)

Считая углы равноточно измеренными с весом 1, находим вес p_i функции j_i

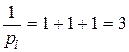
или
p_i =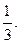

Так как невязки являются истинными ошибками, воспользуемся формулой (2.50)

где N - число треугольников сети триангуляции.

Окончательно имеем

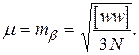(2.53)

Формула (2.53) носит название формулы Ферреро.

2.5.4. Вычисление ошибки единицы веса через отклонения
от арифметической средины

Пусть даны результаты неравноточных измерений

x₁ , x₂ , . . . ,x_n ;

p₁ , p₂ , . . . , p_n ,

а также известны истинное значение X и среднее арифметическое `x₀. Составим два ряда истинных ошибок и отклонений от арифметической средины

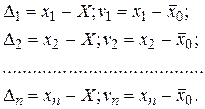(2.54)

Из первого ряда вычтем второй, в результате чего получим

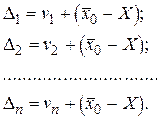(2.55)

Равенства (2.55) возведем в квадрат и умножим на соответствующие веса. Полученные равенства почленно просуммируем и в результате будем иметь

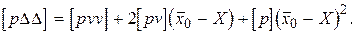(2.56)

В правой части равенства (2.56) второе слагаемое согласно первому свойству отклонений от общей арифметической средины равно нулю. Cледовательно,

(2.57)

Cогласно (2.50) имеем 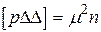, а выражение в круглых скобках является средней квадратической ошибкой среднего значения, т.е.

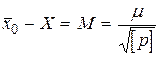(2.58)

или
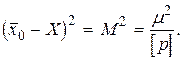(2.59)

С учетом (2.58) и (2.59) равенство (2.57) примет вид

или

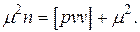
Откуда

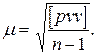(2.60)

Надежность определения m вычислится

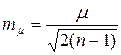. (2.61)