Решение нормальных уравнений по алгоритму Гаусса

Решение нормальных уравнений выполняют в схеме Гаусса (табл. 2).

Для вычисления преобразованных коэффициентов нужно постоянный множитель (-[ab]/[aa]), стоящий в первой элиминационной строке над квадратичным коэффициентом [bb], умножать по строке на вышестоящие числа и складывать каждый раз с элементами второго нормального уравнения

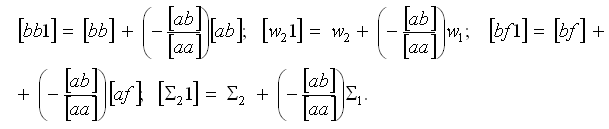
Таблица 2

Схема решения нормальных уравнений коррелат (r = 2; π_i = 1)

Правило развертывания символа Гаусса: "Cимвол развертывается в разность. Уменьшаемое - тот же символ, но со значком на единицу меньше. Вычитаемое - дробь. Знаменатель дроби - квадратичный коэффициент, буква которого соответствует номеру развертываемого символа. Числитель - произведение двух символов, каждый из которых получен заменой буквы уменьшаемого на букву знаменателя".

Последняя коррелата равна числу, стоящему в столбце w последней элиминационной строки. Коррелата к₁ вычисляется с использованием чисел первой элиминационной строки от столбца w налево.

[vv] или [pvv] - для неравноточных измерений - получают как сумму произведений чисел элиминационных строк столбца w на вышестоящие числа того же столбца, знак "минус" отбрасывают:

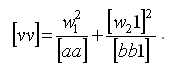(16)

Обратный вес функции 1/P_F получают, как сумму [ff] и произведений чисел элиминационных строк столбца F на вышестоящие числа того же столбца:

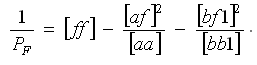
Заключительный контроль решения нормальных уравнений осуществляется подстановкой коррелат в суммарное уравнение:

([aS] - [af])к₁ + ([bS] - [bf])к₂ + ... + ([rS] - [gf])к_r + [w] = 0. (17)