Уравнивание нивелирной сети коррелатным способом

Исходные данные для нивелирной сети, представленной на рис. 1:

Н_А = 100,000 м; Н_В = 110,000 м - отметки исходных пунктов.

h (м): 5,005; 5,015; 5,001 - измеренные превышения.

S (км) : 2; 2; 1 - длины ходов.

p_i = c/S_i: 0,5; 0,5; 1,0 - веса измерений, с = 1 - постоянная .

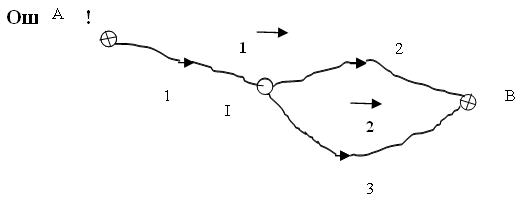
Рис. 1. Нивелирная сеть

Определим число независимых условных уравнений.

Уравнивание нивелирной сети начинают с подсчета числа независимых условных уравнений по формуле r = n - t. В сети, представленной на рис. 1, число измеренных превышений n = 3. Число необходимых измерений t = 1 - количеству вновь определяемых пунктов. Таким образом, r = 2.

Составим условные уравнения связи.

В нивелирной сети имеют место полигонные условия: разность суммы превышений в полигоне после уравнивания и теоретической суммы превышений должна быть равна нулю. Выбирают независимые полигоны - замкнутые или разомкнутые, опирающиеся на твердые пункты, в количестве r. На схеме сети показывают номера выбранных полигонов и стрелкой направление суммирования превышений в полигоне. Если направление хода и напрaвление суммирования превышений в полигоне совпадает, знак у превышения "плюс", если не совпадает, превышение следует взять со знаком "минус".

Условные уравнения связи можно записать в форме (4):

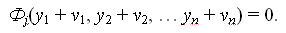
Система имеет вид:

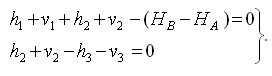(21)

Составим условные уравнения поправок:

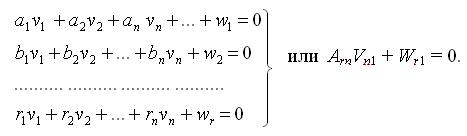
Система (21) линейного вида. Для перехода к условным уравнениям поправок достаточно вычислить невязки, которые следует выразить в сантиметрах или миллиметрах, чтобы порядок коэффициентов и невязок был одинаков.

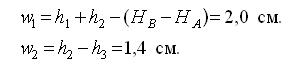
Условные уравнения поправок имеют вид:

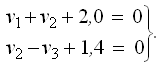(22)

Составим весовую функцию:

F = F(y₁ + ν₁, y₂ + ν₂, ..., y_n + ν_n) = f₀ + f₁ν₁ + f₂ν₂ + ... + f_nν_n.

В качестве весовой функции целесообразно взять отметку определяемой точки и записать ее математическое выражение через измеряемые превышения от ближайшего исходного пункта.

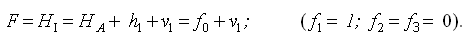(23)

Составим нормальные уравнения коррелат:

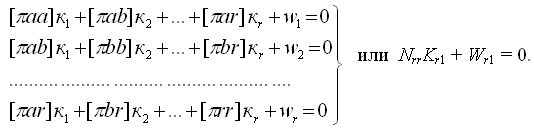
Коэффициенты условных уравнений поправок 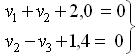и весовой функции F = H_I = f₀ + ν₁ поместим по столбцам (табл. 1) в табл. 3. π_i = 1/p_i - обратный вес результата измерения.

Таблица 3

Коэффициенты условных уравнений и функции

Решим в схеме Гаусса (табл. 4) полученную систему нормальных уравнений коррелат, обратный вес функции вычислим в дополнительном столбце схемы ( табл. 2).

Таблица 4

Решение нормальных уравнений коррелат

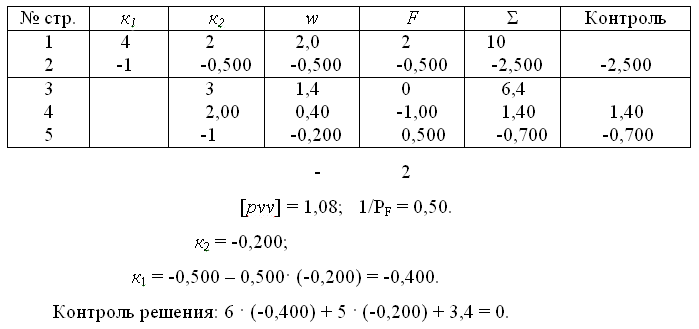
ляемых при решении нормальных уравнений, зависит от тоСледует иметь в виду, что количество запасных знаков, оставчности невязок w и соответствует представленному в данном примере.

Вычислим поправки к результатам измерений:

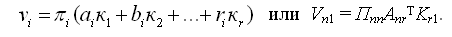
Поправки вычисляют в табл. 3, вначале p_iν_i, как сумму произведений по строке коэффициентов условных уравнений на соответствующие коррелаты, затем ν_i:

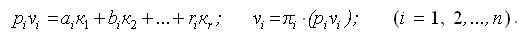
После этого делают контроль поправок: [pν²]= -[кw] и по формуле (16) в схеме решения нормальных уравнений.

Вычислим уравненные значения измеренных величин:

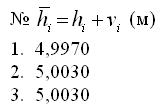
Контроль уравнивания:

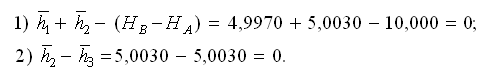
Вычислим отметку определяемого пункта:

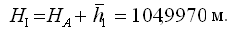
Выполним оценку точности по материалам уравнивания.

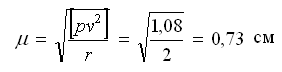
- средняя квадратическая ошибка единицы веса (превышения по ходу в 1 км).

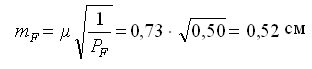
- средняя квадратическая ошибка функции.