Нормальные уравнения

Параметрические уравнения поправок 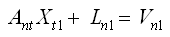решают по СНК, т.е. под условием [pv²] = min, в результате чего получают систему нормальных уравнений:

N_ttX_t1 + B_t1 = 0 (30)

Здесь

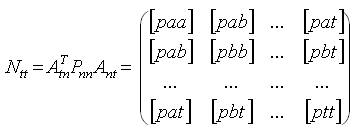
- матрица коэффициентов нормальных уравнений.

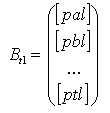
- вектор свободных членов.

Представим систему нормальных уравнений в обычном алгебраическом виде:

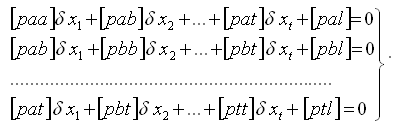(31)

Составление нормальных уравнений

Для составления нормальных уравнений коэффициенты и свободные члены параметрических уравнений поправок помещают в таблицу (табл. 8) по строкам. Пусть t = 2.

Таблица 8

Таблица параметрических уравнений

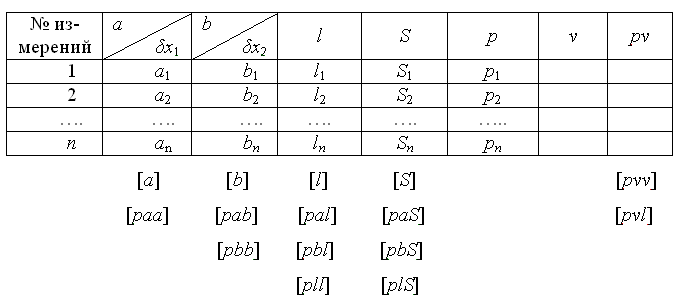
S_i = a_i + b_i + l_i (32)

- контрольные суммы.

[S] = [a] + [b] + [l] - контроль S_i.

Контроль составления нормальных уравнений:

[paS] = [paa] + [pab] + [pal];

[pbS] = [pab] + [pbb] + [pbl];

[plS] = [pal] + [pbl] + [pll].

Весовая функция

Для оценки точности уравненных элементов геодезической сети составляют весовую функцию. Это - функция параметров. Оцениваемую величину выражают через параметры. Функцию приводят к линейному виду разложением в ряд Тейлора.

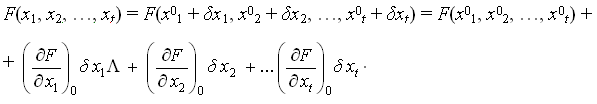
Обозначим

F(x⁰₁, x⁰₂, ..., x⁰_t) = f₀ - приближенное значение функции, обычно не вычисляется;

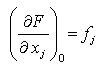- частные производные функции по параметрам;

F = f₀ + f₁δx₁ + f₂δx₂ + ... + f_tδx_t = f₀ + F^T_1tX_t1 (33)

- весовая функция в линейном виде;

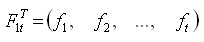- вектор коэффициентов функции.