Решение нормальных уравнений способом обращения
Умножив систему нормальных уравнений NttXt1 + Bt1 = 0 на обратную матрицу N-1
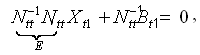
получают:
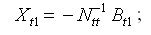 (34)
(34)
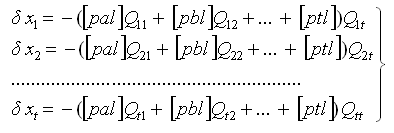 (35)
(35)
- решение нормальных уравнений способом обращения.
По определению обратной матрицы, N-1N = E. Это равенство используется для обоснования способа определения элементов обратной матрицы. Пусть t = 2.
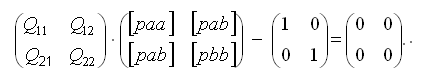
Отсюда следует:
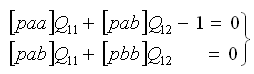 - 1-я система весовых нормальных уравнений.
- 1-я система весовых нормальных уравнений.
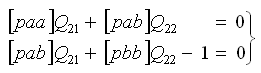 - 2-я система весовых нормальных уравнений.
- 2-я система весовых нормальных уравнений.
В общем случае в результате подобных действий получится t систем весовых нормальных уравнений по t уравнений в каждой системе. Эти системы имеют такую же матрицу коэффициентов, как и основная, с неизвестными δхj и отличаются от нее только столбцами свободных членов. В j-ом уравнении j-ой системы свободный член равен -1, остальные равны нулю. Системы весовых нормальных уравнений решают параллельно с основной системой, в общей схеме, с использованием дополнительных столбцов для свободных членов этих систем (табл. 9).
Таблица 9
Определение элементов обратной матрицы в схеме Гаусса
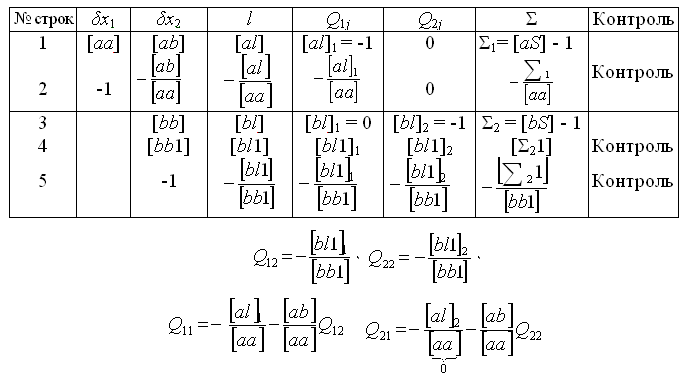
Для контроля вычисленные значения элементов обратной матрицы Qij подставляют в суммарные уравнения, составленные для весовых систем. Например, для t = 2 эти уравнения будут иметь вид:
([paa] + [раb])Q11 + ([pab] + [pbb])Q12 - 1 = 0;
([paa] + [pab])Q21 + ([pаb] + [pbb]) Q22 - 1 = 0.
Для предварительного контроля служат равенства Qij = Qji (i ≠ j).
Элементы обратной матрицы Qij называют весовыми коэффициентами.
Дата добавления: 2016-06-24; просмотров: 872;
