Двухгрупповое уравнивание полигонометрии
Введем в исходную систему условных уравнений (20.1) центральные координаты:
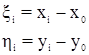
где х0 и у0 – координаты центра тяжести хода, вычисляемые по формулам:
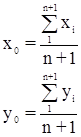
При этом 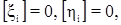 т.к. ξi и ηi представляют собой уклонения отдельных значений от среднего арифметического из них. Вычисление центральных координат по сути соответствует параллельному переносу системы координат, поэтому:
т.к. ξi и ηi представляют собой уклонения отдельных значений от среднего арифметического из них. Вычисление центральных координат по сути соответствует параллельному переносу системы координат, поэтому:
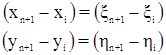
С учетом центральных координат исходная система условных уравнений примет вид:
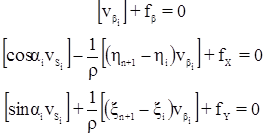 (19.2)
(19.2)
Полученную систему условных уравнений разделим на две группы:
в I группу отнесем условное уравнение поправок дирекционных углов:
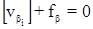 ;
;
во II группу отнесем условные уравнения поправок абсцисс и ординат.
В общем виде условное уравнение поправок дирекционных углов можно записать в виде:
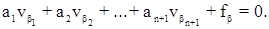
Этому условному уравнению будет соответствовать одно нормальное уравнение коррелат вида:
[qaa] k1 + W1 = 0.
Учитывая, что a1 = a2 = … = 1 и 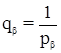 , получаем:
, получаем:
qβ (n+1) k1 + fβ = 0,
откуда:
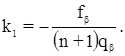
В коррелатное уравнение поправок 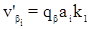 подставим значения ai и ki:
подставим значения ai и ki:
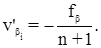
Таким образом, первичные поправки в углы равны невязке с обратным знаком, деленной на количество углов. Полная поправка в измеренные углы будет равна:
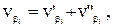
где 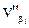 - вторичные поправки в углы.
- вторичные поправки в углы.
Для определения вторичных поправок в углы 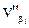 и одновременно поправок в длины линий
и одновременно поправок в длины линий 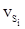 надо совместно решить систему условных уравнений поправок:
надо совместно решить систему условных уравнений поправок:
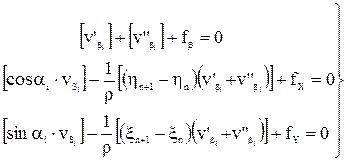 .
.
Из первого уравнения следует, что 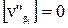 , т.к.
, т.к. 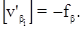 Раскроем круглые скобки во втором и третьем уравнениях:
Раскроем круглые скобки во втором и третьем уравнениях:
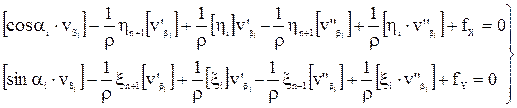
Учитывая, что 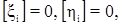
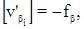 получим:
получим:
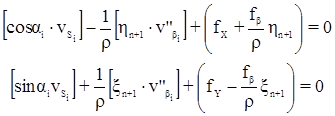
В полученных уравнениях
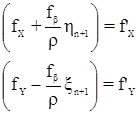
являются преобразованными свободными членами, которые равны невязкам в приращениях координат, вычисленных после введения в измеренные углы первичных поправок. Окончательно получим систему преобразованных условных уравнений поправок:

которую необходимо решить при условии:
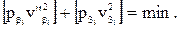
Этой системе условных уравнений соответствует система трех нормальных уравнений коррелат с тремя неизвестными коррелатами – k1, k2 и k3:
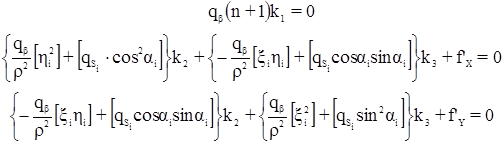 .
.
При этом нормальные уравнения разделились на две независимые группы, т.к. коррелата k1 входит только в первое уравнение, а k2 и k3 – только во второе и третье. Из первого уравнения следует, что k1 = 0, т.к. qβ ≠ 0 и (n + 1) ≠ 0. Обозначим коэффициенты во втором и третьем уравнениях через А, В и С. Тогда:
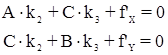
Следовательно:
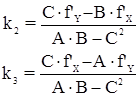
Вторичные поправки в углы и поправки в длины сторон вычисляются по формулам:
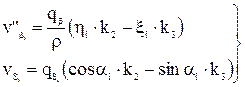
Остальные вычисления выполняются аналогично коррелатному уравниванию:
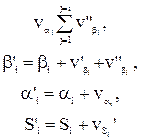
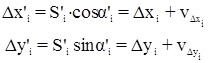 ,
,
где 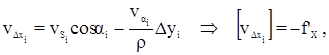
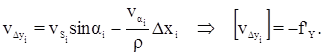
Дата добавления: 2016-06-02; просмотров: 1546;
